动手折出精彩 思考凸显价值

    钱旭东

    

    

    

    [摘? 要] “折纸与证明”是苏科版数学教材中的一个数学活动，这一活动给学生提供了探索的空间. 对教材进行深入挖掘的基础上，笔者改进和丰富了课本上的探究活动，使数学活动针对性更强，更容易展开，也更能激发学生兴趣，从而为学生搭建了一个探索的平台. 在探索中，师生一起经历了观察——测量——猜测——说理的过程，培养了能力，提升了素养.

    [关键词] 折纸;证明;平行四边形;数学活动

    背景

    本节课是一节数学探索活动课，在课时安排上是位于苏科版数学教材八年级下册第9章“中心对称图形——平行四边形”全章的最后一节课.

    笔者在本章内容的最后安排这样一节探索活动课，主要是基于以下两点考虑：一是通过学生的探索活动能让本章的主要知识在运用中得到复习巩固;二是通过学生的动手操作，培养他们的探索精神，并在探索的过程中体会到探索的乐趣.

    本节课由于准备充分，课堂效果良好，学生探索气氛浓厚，兴趣盎然，达到了预期的目的.

    教材及学情分析

    在苏科版数学教材八年级下册第9章“中心对称图形——平行四边形”中，每节的开始部分都为学生安排了“操作”“讨论”“思考”等环节，而在“操作”环节中又多以图形的旋转、翻折和平移为主，这是“做中学”的教育理念在教材中的生动体现. 同时，这也在无形中培养了学生积极动手、努力探索的良好学习品质，为本节数学探索活动课打下了非常好的基础. 有了这样的教材安排和学生的活动基础，当学生在课堂上折叠矩形纸片时，他们有兴趣而不陌生，有挑战而不畏难.

    在上本节课之前，学生已经学完了本章的基本知识，学习了中心对称和中心对称图形，平行四边形的判定和性质，有了矩形、菱形和正方形的相关知识，也学习了三角形的中位线知识，这些知识的学习为学生继续深入探索矩形纸片的折叠提供了必要的知识储备. 此外，学生由于有了前面每节学习中图形翻折的经历，在心里也会对“图形的翻折还会出现什么规律和性质”出现隐性的心理期待，有继续探索下去的愿望. 这时，教师应该做的就是努力为学生搭建继续探索的平台.

    本节课的内容在教材中并没有安排，但是新的课程理念认为，教师在教学中应该是用教材教而不是教教材，对教材进行创造性处理的能力应该是现代教师的必备素质. 在实际的教学过程中，我们应该认真钻研教材，充分使用教材，但绝不能因为只满足于教教材，囿于教材，机械套用而失去教师的创造性.

    教学过程实录

    1. 探索一

    师：现在大家手上都有一张矩形纸片，请你折叠一次，将纸片折叠为两块面积相等的图形. 大家试试看.

    学生动手折纸，教师来回观察学生的操作情况.

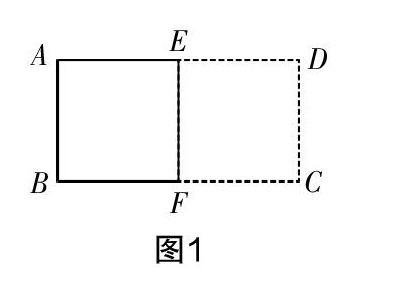
    生1：我这样把纸片对折（如图1）.

    [图1]

    生2受生1启发，立即说：那我也可以这样叠（如图2）.

    [圖2]

    师：大家说，这两位同学叠的对吗？

    大家齐声回答：对.

    师：请同学们思考一下，这两位同学的折法说明矩形是一个什么样的图形？

    短暂的沉默后，有学生小声说：轴对称图形.

    师：对，这位同学的回答非常正确！大家还有什么叠法？

    很多同学举手，争着发言.

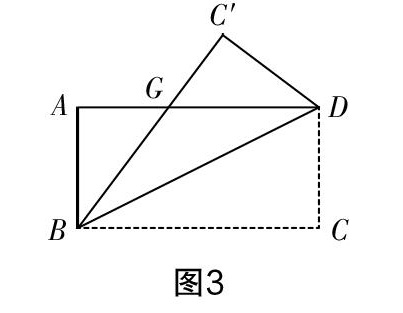
    生3：折成图3.

    [图3]

    生4：折成图4.

    [图4]

    师：大家观察前面这几种折法，它们的折痕有什么共同特点吗？

    生5：矩形是中心对称图形，这些折痕都经过矩形的对称中心.

    师：非常棒！大家还有什么叠法吗？

    学生受到启发，折叠方式越来越多. 教师在大屏幕上显示几种典型的叠法（图5、图6）.

    [图6]

    师：同学们都是折纸高手啊！有这么多的折法.

    评注? 探索的起点低，学生容易入手，不同的学生都可以探索出不同难度的折叠方法. 学生在动手操作的过程中，切实感受矩形轴对称和中心对称的性质. 同时，在探索的起始阶段安排难度较小的探索，对激发学生的自信心和维持探索的兴趣都有好处. 这也为后面继续探索打下了基础.

    2. 探索二

    师：请大家观察图5，除了折叠出的两块面积相等之外，图形中还有哪些相等的关系.

    生6：AB=C′D′，BF=D′E.

    生7：AG=C′G.

    师：很好，两位同学找的是线段之间的关系. 还有吗？

    生8：∠GFE=∠GEF.

    生9：GF=GE. 因为上图中由折叠知道∠CFE=∠GFE，而∠CFE=∠AEF，所以GF=GE.

    师：非常好！类似的，在图3和图4中是否也存在BG=DG和AE=AF？

    学生齐答：存在.

    师：请大家观察图3，在图中除了BG=DG外还有哪些数学结论？

    生9：我觉得△ABG和△C′DG全等.

    师：能说明理由吗？

    生9：我由前面同学的回答可以知道BG=DG，又在矩形中AB=CD=C′D，且∠A=∠C′=90°，所以△ABG≌△C′DG.

    师：说得非常好！现在如果我把纸片折叠成图7的形状，是否也有GF=GE.

    [图7]

    学生短暂思考后，一起回答：GF还是等于GE.

    师：好，请大家用我们探索出的结论解决这样的问题：如果在图3中，矩形一边AD=8，另一边AB=6，求AG的长度.

    题目有难度，学生思考中.

    师：请问AG与BG的和是多少？

    生齐答：就是AD长，为8.

    师：如何把AB=6这个条件用上？线段AB，AG和BG之间有什么关系吗？

    生齐答：满足勾股定理！（解答略）

    师：作为练习，大家试着解决这样的问题：在图4中，矩形一边AD=8，另一边AB=6，求BE的长度. （解答略）

    评注? 探索的内容由图形的形状重合关系转变为图形中包含的线段、角之间的数量关系，探索更加深入. 在探索中，学生在教师的引导下经历了从特殊到一般的探索过程，体会到探索过程中包含的数学知识，如和平行线有关的性质、三角形全等、勾股定理、矩形的性质等等. 教师不仅给学生搭建了探索的平台， 还努力搭建让学生运用探索出的结论去解决问题的平台. 这种在操作中探索，在探索中运用的做法，蕴涵了“做中学”的教育理念.

    3. 探索三

    师：请同学们将手中的矩形纸片按照下面图8到图10的步骤折叠.

    师：从图8到图10，经过了两次折叠. 请同学们在动手折叠时注意体会折叠过程中图形位置与数量关系的变化.

    师：在图9中，△AEB′是什么三角形？

    生齐答：是等腰直角三角形.

    师：请观察图10，其中有几个等腰直角三角形？

    生10：我看有三个，它们是△A′B′E，△A′DF，△CEF.

    师：能解释一下吗？（解释略）

    师：如果矩形ABCD的一边AB=6，另一边AD=10，请求出△CEF的面积.

    生11：由折叠可知，CE=4，而△CEF是等腰直角三角形，所以其面积为8.

    师：△A′DF的面积可以求吗？

    生12：和求△CEF的面积类似，可以求出△A′DF的面积是2.

    评注? 探索纸片的折叠由一次折叠到多次折叠，探索的难度更大，对学生也提出了更大的挑战，可以看出探索在难度上是循序渐进的. 而同样是多次折叠，前面一个探索比后面的探索难度要小，也更容易入手去完成，在同类型的探索中，其难度也是有梯度的. 在探索中，学生和教师一起经历了观察——测量——猜测——说理的过程. 学生的探索不是一帆风顺的，在学生遇到困难时，教师并没有直接抛出结论，而是启发学生将多次折叠转化为一次折叠，在探索中渗透了化归思想，培养了能力，提升了素养.

    4. 课后探索（作业）

    师：本节课我们一起对矩形纸片的折叠进行了比较深入的探索，用我们学习的知识解决了许多问题. 其实在矩形纸片中还包含了很多的数学奥秘，这些奥秘会在我们以后的学习中不断去发现. 课后，请同学们继续探索下面的几个问题.

    问题1：如图14，将矩形ABCD中D点折叠至BC上的F点处，折痕经过点A. 请问除直角外，图中还有哪些相等的角？有哪些边是相等的？如果AB=8，AD=10，求DE的长.

    [图11]

    问题2：如图12，将一细长的矩形纸条打结后拉直压平，请观察、测量后进行猜测，线段AB，BC，CD，DE，EA是否都是相等的？结合你折叠的纸片说明理由. 此外，在图12中你还能发现哪些结论？写出你的发现，和同学交流一下.

    [图12]

    评注? 这样的探索型作业使得学生的探索活动由课内延伸到了课外. 两道探索题在难度上有梯度. 同时对每一题而言，不同的学生通过探索都会有不同的收获，得出自己的结论. 这和课堂上的探索题遥相呼应，是整个探索活动的有机组成部分，给人一种知识无穷，探索不止的思考韵味.

    教学反思

    苏科版教材中，很多章节中都安排了“读一读”“閱读”和“数学活动”等内容，这些内容的安排一方面丰富了教材的文化内涵，开阔了学生的视野，另一方面也为教师创造性使用教材提供了广阔的空间. “折纸与证明”是苏科版数学教材中的一个数学活动，这一活动给学生提供了探索的空间. 在对教材进行深入挖掘的基础上，笔者改进和丰富了课本上的探究活动，使数学活动针对性更强，更容易展开，也更能激发学生兴趣，从而为学生搭建了一个探索的平台.

    在整个课堂上，学生探索兴趣浓厚，动手能力强，参与程度高. 从本节课可以看出学生有探索的能力，也有探索的欲望. 而反思以前的教学，我们对学生是真正了解了吗？我们有多少教学是从学生的需要出发的？在组织教学时，我们给学生探索的空间了吗？这些问题都值得教师去思考.

    在本节课的教学过程中，学生的想法很多，而笔者仅仅从教学进度考虑没有充分展示学生的想法，使得有些探索不够深入. 而当难度加大的时候，也没有留给学生充分的时间去探索，而是忙于启发，担心学生的探索能力，怕探索时间长会影响教学进度. 认真反思会发现，课堂上教师经常会为了自己的教学时间、内容等方面去控制学生的活动，不管效果如何，这都是教师为自己考虑，而不是发自内心从学生的发展考虑. 这种教师头脑中内隐的观念对学生的发展和对自身的提高都不利，教师应当在教学中多反思，不断更新自己的观念.

    从课前的准备到课堂的教学实施，从教材的钻研到学生学习情况的把握，一路反思，感受很多. 教师在备课钻研教材时，不仅要研究本节课的内容，更要对教材中的整章内容有全局的认识，要善于对教材进行再加工，切实从学生的发展着想. 当然，创造性地处理和使用教材对教师提出了更高的要求，教师的工作难度也会加大，但是教师在教学中创造性地处理和使用教材更符合学生的发展需求，也更符合教材编写者的编写意图，同时这对教师自身的发展也有很大的好处.