整体意识:完善思维结构的一剂良方
马奇
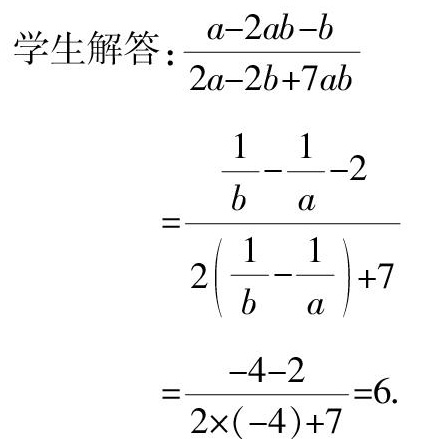
[摘? 要] 文章以一堂整体思想习题课实录为例,探讨习题课中,如何渗透整体意识,以达到完善学生思维结构的目的.
[关键词] 整体意识;思维结构;初中数学;运算能力
数学运算是数学核心素养之一,培养学生的运算能力是初中数学教学的目标之一. 因此,在数学教学中,运算能力培养是数学教师的核心任务[1]. 然而,在日常教学中,我们发现:初中学生的运算能力不容乐观,“小错天天有,大错三六九”,归根结底是学生对问题的观察能力不够,分析能力不够. 因此,教师有必要调整教学策略与方法,把运算能力的培养作为数学教学的首要任务. 数学思想是数学的灵魂,也是解题的法宝. 有道是:数学解题,思想先行. 整体思想,是数学解题的重要思想方法之一,是简化运算、优化解题过程的助推器. 然而,学生却不善于利用这种思想. 因此,教师在教学中应渗透整体意识,以达到完善学生思维结构的目的. 为此,笔者在中考复习阶段,给学生上了一堂应用整体思想解题的习题课,下文就是这堂课的实录.
课堂实录
1. 引入例题,认知整体思想
【引例】已知-=4,则的值等于(? ? )
A. 6? ? ?B. -6? ? C.? ?D. -
教师点拨:根据条件显然无法计算出a,b的值,只能考虑在所求代数式中构造出-的形式,再整体代入求解.
学生解答:
=
==6.
教师提问:本题也可以将条件变形为b-a=4ab,即a-b=-4ab,再整体代入求解. 这种解题方法体现了数学解题中的哪种思想?
众学生:整体思想.
教师:对!整体思想,整体思想是指在研究和解决有关数学问题时,通过研究问题的整体形式、整体结构、整体特征,进而对这个问题进行整体处理,它是一种解题方法,更是一种数学思想[2]. 从整体上去认识问题、思考问题,常常能起到化繁为简、变难为易的作用. 这种思想的应用能训练大家思维的灵活性. 我们遇到的整体思想主要有:整体代入、整体加减、整体代换、整体联想、整体补形、整体改造等等. 整体思想不仅在代数问题中应用广泛,在几何问题中也大有用武之地. 只要我们善于观察,就一定能从题目中捕捉到“整体思想”的信息.
2. 小试牛刀,应用整体思想
师:既然整体思想为我们解题打开了快捷的绿色通道. 那么让我们一起来感受一下它的神奇魅力吧. 请同学们合作完成下面几个问题,并选几位交流.
题1已知关于x,y的二元一次方程组3x-ay=5,
x+by=11 的解为x=5,
y=6, 那么关于x,y的二元一次方程组3(x+y)-a(x-y)=5,
x+y+b(x-y)=11的解为______.
题2已知+4
+=,求1872+48
的值.
10分钟后,教师请两位学生上讲台交流并展示.
学生1:对于题1,如果把x=5,
y=6代入3x-ay=5,
x+by=11,解出a,b的值,再代入3(x+y)-a(x-y)=5,
x+y+b(x-y)=11进行求解,应当是可行的,但运算量比较大,相对而言比较烦琐.
解:在方程组3x-ay=5,
x+by=11中令x+y=m,
x-y=n,则此方程组变形为3m-an=5,
m+bn=11,对照第一个方程组即知m=5,
n=6,从而x+y=5,
x-y=6,容易得到第二个方程组的解为
x=,
y=-,这样就避免了求a,b的值,又简化了方程组,简便易操作. 故本题答案为:
x=,
y=-.
学生感悟:本题通过整体加减既避免了求复杂的未知数的值,又简化了方程组,解答直接简便.
学生2:对于问题2,如果我们把题目中的x看成一个未知数来求,然后将它代入1872+48
中求值,计算量非常大,最终结果可能会导致“无功而返”,如果我们把+看成一个整体,通过通分得到,再把它看作一个整体,取其倒数就是,利用这种思路解答,本题就变得轻而易举了.
解:因为+4
+=,即+4
=,故4
= ,则=,所以=. 把=代入得1872+48×=2000.
学生感悟:从本题的解答可以看出,整体思想与换元法类似,把某一部分看作一个整体来处理,能让我们少走弯路,直达目的地.
师:两位同学的分析、解答和感悟都十分精彩,我们为他们的精彩發言鼓掌. (学生热烈鼓掌)
3. 自主练习,升华整体思想
我的课堂我做主. 学生已经初步认识了整体思想在解题中的重要性,接下来,教师要求学生自己查阅资料,找到体现整体思想的练习题,并说出自己的解题感受,允许小组合作完成. 在学生探讨问题时,教师巡视,并回答学生随时提出的问题. 十分钟后选择部分学生交流发言.
学生3: 我说一个代数式求值问题:已知a-b=b-c=,a2+b2+c2=1,求ab+bc+ca的值.
本题用常规思路做,就是由已知条件求出a,b,c的值,再代入待求式计算,解答过程十分烦琐,而注意到由a-b=b-c=可先求出a-c的值,再将ab+bc+ca变形,用a2+b2+c2、a-b、b-c及a-c来表示,这样整体代入之后题目就变得简单多了,解答如下:
由a-b=b-c=,可以得到a-c=. 由(a-b)2+(b-c)2+(a-c)2=2(a2+b2+c2)-2(ab+bc+ac)得到 ab+bc+ca=(a2+b2+c2)-[(a-b)2+(b-c)2+(a-c)2],将a2+b2+c2,a-b,b-c及a-c的值整体代入,可得ab+bc+ca=1-
2+
2+
2=1-×=-.
学生4:我举个数值比大小的例子:若M=123456789×123456786,N=123456788×123456787,试比较M与N的大小.
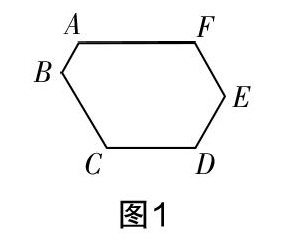
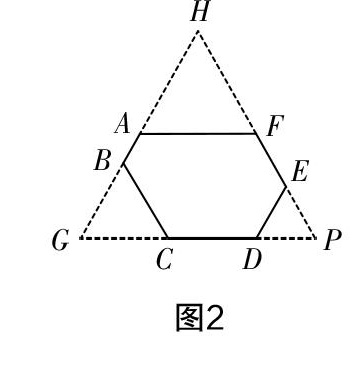
本题的数值较大,求出后再比较大小显然行不通. 我通过仔细观察发现,这些数都在123456788左右波动,于是不妨将123456788看成一个整体用a代换,于是123456789=a+1,123456786=a-2,123456787=a-1,于是M=(a+1)(a-2)=a2-a-2,N=a(a-1)=a2-a,故M-N=(a2-a-2)-(a2-a)=-2<0,由此可得M 学生5:刚才两位同学举的例子都是代数问题中的整体思想的应用,我认为几何问题中也可以应用整体思想,从而让解答更精彩. 我举例如下:如图1,六边形ABCDEF的六个角都相等,若AB=1,BC=CD=3,DE=2,则六边形ABCDEF的周长等于______. 对于这题,我是这样处理的:分别作线段AB,CD,EF的延长线和反向延长线,使它们交于点G,H,P,如图2. 因为六边形ABCDEF的六个角都等于120°,故六边形ABCDEF的每个外角都是60°,故△AHF、△BGC、△DPE、△GHP均为正三角形. 于是GC=BC=3,DP=DE=2, GH=GP=GC+CD+DP=3+3+2=8,FA=HA=GH-AB-BG=8-1-3=4,EF=PH-HF-EP=8-4-2=2. 故六边形ABCDEF的周长为:1+3+3+2+2+4=15. [图2] 本题采用了整体补形思想,我根据已知图形的特点,将不规则或不完整的图形,通过简单的拼接,补充成规则的或完整的图形,从而将它转化为规则图形加以解决. …… 下课铃响起,学生们却意犹未尽,笔者只好让学生把自己找的相关题目作为今天的作业,明天课上继续交流. 一点感悟 阿基米德曾经说过:“给我一个支点,我就能撬起地球. ”学生在数学学习中,这个“支点”由谁给呢?当然是教师. 教师是课堂教学的组织者、指导者与参与者,更是学生课堂活动的策划者与学生思维的引领者. 平时我们经常埋怨学生,这道题做了很多次还是不会做. 是学生真的不会做,还是教师根本没有教会他?这个问题值得深思. 利用整体思想解题一直是学生的弱点,遇到复杂的问题,他们往往感到茫然. 笔者认为,造成这种现象的原因是教师没有在恰当的时机加以引导与启发. 教师教给学生的知识往往是零散的,没有整体性,因而导致学生思考问题过于片面,只见树木,不见森林,真可谓“不识庐山真面目,只缘身在此山中”. 要彻底改变这种现象,教师应在教学中不断渗透整体思维,帮助学生搭建知识结构和思维框架,如引进思维导图,教师可以课堂上提出一个中心问題,让学生全方位地整体思考,相互补充,就像本节课,不仅激发了学生的学习热情,吸引每个学生参与到课堂活动中来,而且随着问题的解决,学生的整体意识被激发,思维能力也有了很大的提高. 参考文献: [1]吴海宁. 体悟数学:让数学核心素养的种子在课堂中萌发——以“6.1线段、射线、直线”一课为例[J]. 中学数学杂志,2019(02). [2]张新志,周春霞. “合一”何须“分二”——例谈数学解题中的“整体”策略[J]. 中学数学研究(华南师范大学版),2019(01).

