关注学生发展 实施单元教学
沈华
[摘? 要] “单元教学”“关注初中生学力发展”都源于李庾南老师的“自学·议论·引导”教学法,是指基于学生已有的基础,以提升学生学力为宗旨,打破按课时分配的小段教学,对学材进行加工、重组,灵活组织单元教学内容的教学方法. 将单元教学与学生发展需求相结合,这是我校近期深入探究的一项课题.
[关键词] 单元教学;学生发展需求;初三复习课;三角形
数学知识的教学,要关注知识的“生长点”和“延伸点”,把每节课的教学内容放在整体知识体系中,注重知识的结构与体系,处理好局部知识和整体知识的关系,引导学生感知数学知识的整体性[1]. 课程标准指导我们一线教师在教学过程中要考虑知识的整体性,不要把某些整体的知识碎片化,要实施单元教学. 在实施单元教学时,不仅要考虑对教材内容的有机整合,也要考虑学生的发展需求,教学过程就是在教师的引导下,不断地将学生的“最近发展区”转化为现有的发展水平,向潜在的发展水平提升,是一种螺旋式发展的过程[2]. 笔者参加海门市初三复习课研讨活动,并执教了人教版初三复习课“三角形”,尝试立足于学生发展需求,通过单元教学,整合初中数学有关三角形的知识(三角形的边、角、勾股定理、锐角三角函数、等腰三角形,以及全等三角形、相似三角形的关系),整体理解三角形相关知识,力争取得较好的教学效果.
教学流程及设计意图
1. 通过运算,弄清基础知识
师:今天我们研究的“对象”是三角形,它有哪些基本元素?
生:线段、角,其中三角形中的线段包括三角形的边及三条重要线段:中线、角平分线、高线.
今天我们就从三角形的边、角出发,逐渐增加其条件,丰富其情节,复习与三角形有关的知识.
活动一:算一算
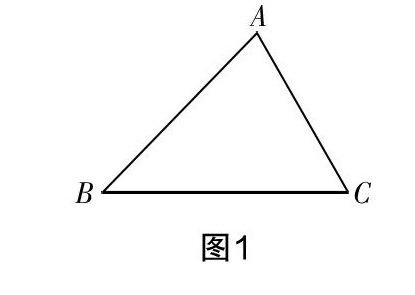
问题:如图1,在△ABC中,∠A=70°,你能求出∠B的度数吗?若不能的话,你能添加一个条件,求出∠B的度数吗?你有哪些不同的方法?
[图1]
生1:只给出一个条件∠A=70°,只能得到∠B+∠C=110°,而不能得出∠B的度数.
生2:增加一个条件,如“∠C的度数为60°”,利用三角形的内角和得∠B=180°-70°-60°=50°;或者增加“∠C的外角=120°”这一条件,利用外角等于和它不相邻的两个内角的和来求出∠B的度数.
生3:增加一个条件是∠B与∠C的数量关系,如“∠C=3∠B”,由已知条件得∠B+∠C=110°,这样得到关于∠B,∠C的方程组,从而求出∠B.
生4:增加一个条件是“△ABC为等腰三角形”,这样要分情况讨论:若∠A为顶角,则∠B=(180-70)÷2=55°;若∠A为底角时,∠B为底角的话,∠B=∠A=70°;∠B为顶角的话,则∠C为底角=70°,∠B=180-70-70=40°.
师追问:若∠A=100°呢?
生5:∠A为钝角,只能作为等腰三角形的顶角,故只有一种情况,∠B=(180-100)÷2=40°.
生6:增加一个条件是“△ABC为直角三角形”,这样也要分情况讨论:∠B若为直角,则∠B=90°;若∠C为直角,则∠B=90-70°=20°.
设计意图? 基于学生已有的基础,特别是数学基础较薄弱的学生,设置低起点的问题,以激发所有学生学习的积极性. 通过以简单问题为引导,设计开放型问题,学生独立思考,个别回答,其余学生补充,教师适时追问等形式,让学生弄清利用三角形的内角和定理来解决一般三角形、等腰三角形、直角三角形中有关角的计算,总结出分类讨论、方程思想等数学思想方法.
活动二:求一求
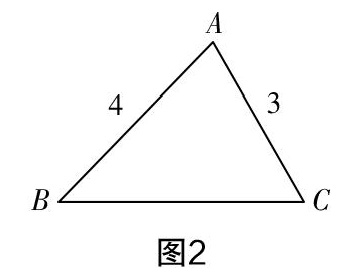
问题:如图2,在△ABC中,AB=4,AC=3. BC边的取值范围为______;你能求出BC的长吗?你能添加一个条件,求出BC的长度吗?你有哪些不同的方法?
[图2]
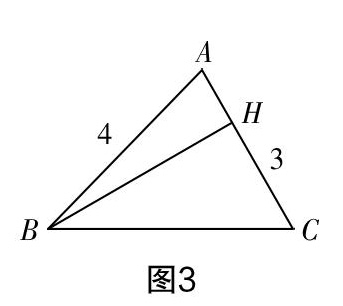
生7:求不出BC的长,但根据三角形的三边关系,两边之和大于第三边,两边之差小于第三边,有4-3 生8:添加一个条件“∠A=90°”,则利用勾股定理得BC===5. 师追问:若条件改为△ABC为直角三角形呢? 生9:此时没有明确哪个角是直角,所以要分类讨论:当∠A为直角时,BC=5;当∠C为直角,则AB为斜边,BC===;AC不是最大的邊,∠B不可能为直角,所以BC的长为5或. 生10:类比刚才老师的提问,可以添加一个条件“△ABC为等腰三角形”. 同样要进行分类讨论:若AB,BC为腰,则BC=4;若AC,BC为腰,则BC=3,所以BC=4或BC=3. 师追问:若△ABC为等腰三角形,条件改为AB=4,AC=2呢? 生11:同样要进行分类讨论:若AB,BC为腰,则BC=4;若AC,BC为腰,则出现AC+BC=2+2=4=AB,AB,AC,BC不能组成三角形,所以BC的值只能为4. 生12:添加一个条件“∠A=60°”. 作BH垂直AC于点H(如图3),在Rt△ABH中,可得AH=2,BH=2,所以CH=AC-AH=3-2=1,在Rt△BCH中,利用勾股定理得BC===. [图3] 师追问:已知△ABC中,AB=4,AC=3.若添加的条件为∠B=30°,BC长度为多少呢? 生13:过点A作AH垂直于BC于点H(如图4), 在Rt△ABH中,可得AH=2,BH=2,在Rt△ACH中,利用勾股定理得CH===,所以BC=BH+CH=2+. [图4] 生14:还有一种情况,如图5所示,此时BC=BH-CH=2-. 所以BC长为2+或2-. [图5] 设计意图? 基于学生已有对三角形三边关系、勾股定理、特殊角的三角函数等知识的掌握,通过条件开放以激发所有学生学习的积极性. 通过以开放型问题为引导,学生独立思考,若有困难可进行小组交流讨论,教师适时追问,变式等形式,让学生弄清三角形中有关线段计算的常见类型,总结出通过作高,把一般三角形转化为直角三角形的“化斜为直”的方法,以及三角形的高在形内和形外的“分类讨论”思想. 2. 变式引领,拓展关联知识 活动三:变一变 在△ABC中,AB=4,AC=3. (1) 如图6,AD为高,且AD=,则BC=______. [图6] 变式1:若还是这个条件,没有给你图,你会求BC的长吗? 变式2:你会求三角形ABC的面积吗? 变式3:求出某些角的三角函数值. (2)如图7,AD为三角形的中线,则S ∶ S=______;AD的取值范围为______. [圖7] 变式1:如图7,取AC的中点E,连接BE,交AD于点O,连接DE,在这个图中你能得到哪些有关三角形以及边、角的结论? 变式2:若△ODE的面积为1,你能求出图中哪些三角形的面积? (3)如图8,AD为角平分线. [图8] ①点D到AC,AB的距离是什么数量关系? ②S ∶ S=______. 变式1:若S=4,则是S=______. 变式2:BD ∶ AD=______. 设计意图? 基于学生对三角形中重要的三条线段:高、中线、角平分线的理解与掌握,通过合理的变式,串联起初中阶段与之相关的知识点,化零碎为整体. 第(1)题以三角形的高有关问题为引导,复习三角形的面积、勾股定理、三角函数等相应知识,没有明确高的位置,要分形内和形外,提炼出“分类讨论”的思想. 第(2)题以三角形的中线有关的开放型问题为引导,弄清中线的定义,倍长中线构造全等三角形等常用方法. 通过变式1,复习三角形的中位线、相似、位似的定义、性质及应用,可以得出如DE ∶ AB,BO ∶ OE,AO ∶ OD,S ∶ S, S ∶ S 等结果;通过变式2,可以得出各三角形面积与底之比、高之比的关系. 第(3)题以三角形的角平分线有关的问题为引导,利用角平分线的性质,得出两三角形高相等时,面积比等于底之比,变式2是在高相等时,底之比等于面积比. 3. 反思提升,构建知识结构 活动四:讲一讲 (1)体会本节课我们是以三角形的什么基本元素为基础展开研究的?具体研究了三角形哪些内容? (2)通过本节课的复习,你积累了哪些数学思想、数学方法? 设计意图? 通过反思总结,学生说出本节课所研究的内容,师生共同搭建本节课的知识框架图,使得初中阶段与三角形有关的内容通过单元教学,清晰地呈现在师生面前,由零碎的知识点到网状的知识框架图,完成“由点到网”的学习过程. 教后反思 本节初三复习课的教学,不是传统的用大量题目来回顾、复习相应的知识点,而是通过一个基本的三角形,知道某些角或边的量,逐渐添加条件,通过变式、追问等形式,引导学生对相应知识进行回顾、巩固以及综合运用. 学生学力的生成、发展呈现出自主性、开放性、发展性、综合性等特点[3]. 高效复习课应从以下角度思考,从而提高学生的学力. 1. 基于学生发展需求 学生发展需求是指学生在学习过程中提升自我能力的一种欲望. 这一欲望首先建立在已有知识的基础上,教学时要基于学生已有的知识,低起点,缓坡度,螺旋式逐步渐进提升,这样有利于培养学生思考问题的积极性,增强学生的自学能力,建立良好的认知结构,培养、发展数学思维方法和能力. 2. 精选例题,变式引领 初三的复习课,不同于普通章节的复习课,涉及的知识点多、杂,不能靠大量的题目来复习相应的知识点,例题的精选显得尤为重要. 以例题为起点,带动本节课的基础知识点,通过条件开放、变式引领,让学生有更多考虑问题的角度,充分发挥学生的主体作用,复习步步深入,达成本节课的复习目标. 3. 构建单元教学框架图 初三复习课通过知识框架图将相应的知识网状化、系统化,让学生对该单元知识的认识更深入、深刻,感知各个知识点不是零散的、孤立的,而是相互有联系的,让学生从整体视角下理解各知识点,有利于对知识的记忆,提高自身的数学能力. 总之,在初三数学复习教学中,一定要基于学生的发展需求,以学生为教学主体,精心设计例题,强化知识结构,在教师的引导下,最大限度地提高复习效率. 参考文献: [1]中华人民共和国教育部. 义务教育数学课程标准(2011年版)[M]. 北京:人民教育出版社,2012. [2]李庾南. 自学·议论·引导教学论[M]. 北京:人民教育出版社,2013. [3]李庾南,陈育斌. 中学数学新课程教学设计30例[M]. 北京:人民教育出版社,2007.

