折纸艺术介入数学课堂的课例研究
于庆
[摘? 要] 本课例是将折纸艺术介入数学课堂的大胆尝试,完美的白银比例让一张普通的A4纸具有神奇的特征和用处,其中蕴含着丰富的数学原理. 两张规则完整的正方形纸不粘、不剪,简单的错位嵌套后就能折成一个牢固完整的正方体造型. 让学生感受数学特有的艺术魅力,对激发学生的数学学习兴趣具有积极的作用.
[关键词] 白银比例;白银长方形;折纸;数学课堂
艺术与数学有着密不可分的联系,艺术源于数学,数学赋灵感于艺术. 创新地向学生传播数学所具有的艺术价值,能使今后在向学生进行数学教学时取得较好的效果. 本课例是将折纸介入数学课堂的大胆尝试,生活中常见的纸张体现了人们生活的智慧,能够培养学生的生活创新意识.
从生活中常见的A4纸激趣导入
我们日常生活中最常用的纸就是A4纸,你知道它有什么奇妙的特征吗?你知道它的长和宽分别是多少厘米吗?它的长与宽的比例又是多少呢?或许你认为它的长宽比应该是黄金分割比,真的是这样吗?你可以在电脑中打开一个Word文档,找到“页面布局”的菜单栏,在“纸张大小”的下拉列表中选择A4时,就会看到Word中A4纸的规格是21 cm×29.6 cm,A4纸长与宽的数值为什么不按习惯取整数而是小数呢?原来A4纸是由国际标准化组织的ISO 216定义的,规格为21 cm×29.7 cm,世界上多数国家所使用的纸张尺寸都是采用这一国际标准. A4纸的长宽比为29.7÷21≈1.414,这显然不是黄金比例(golden ratio),那这个与黄金比例1.618十分接近的比例是什么数呢?正是无理数的近似值.
A组纸张具有两个特征:一是所有A0、A1、A2、A3…尺寸纸张的长宽比都同为,二是A0纸对裁可以得到2张A1纸,A1纸对裁可以得到2张A2纸,依此类推. 事实上,并不是任意一张纸对裁,都可以得到长宽比跟原来的纸相同的两张纸,只有A组纸张特殊的长宽比才能带来这种特性,这两个特色让A组纸张非常好用,不但剪切方便,而且没有浪费,应用广泛. 所以,人们将1.414称为白银比例(silver ratio)或白银分割,并将具有白银比例的长方形称为白银长方形,其命名和黄金比例类似.
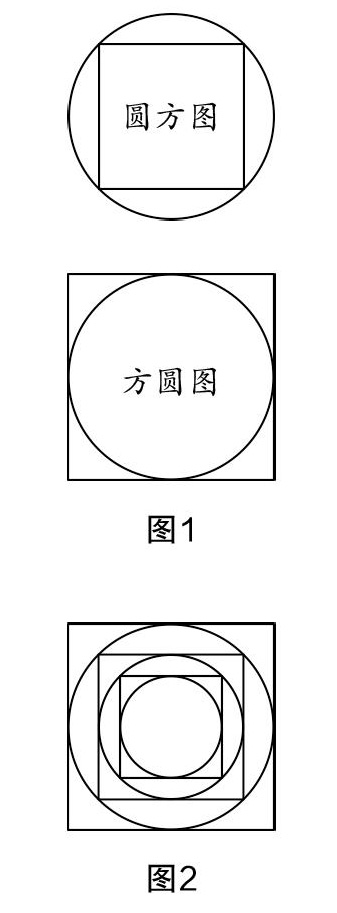
如果说黄金分割比是西方人最钟爱的比例,那么中国人对比例之美的追求就是白银分割比. 我们常说的“没有规矩不成方圆”这句话其实源自中国古人“天圆地方”的宇宙观. 如图1的“圆方方圆图”,一个圆套方,和一个方套圆,你能发现其中暗藏着什么比例的玄机吗?其实就是1∶,“圆方图”中小正方形的边长与其外接圆的直径或对角线的比是1∶,在这个外接圆外再画一个大正方形就得到“方圆图”,“圆方图”中小正方形的边长与“方圆图”中大正方形的边长比也是1∶,如此继续画正方形的外接圆和圆的外接正方形,反反复复运用圆方方圆图就可以得到一个很精彩的正方形构图(如图2). 白银比例也是当代造型艺术中常用的比值,它比黄金比例更有“人文科技感”. 然而,从美学上说,,,也都最符合日常视觉的习惯,但还是白银比例实际利用起来更方便.
课例从生活中常见的A4纸引入,让学生领略其中蕴含的数学原理与数学在生活中应用的价值.
尝试用数学折纸的方法验证
A4纸的长宽比例
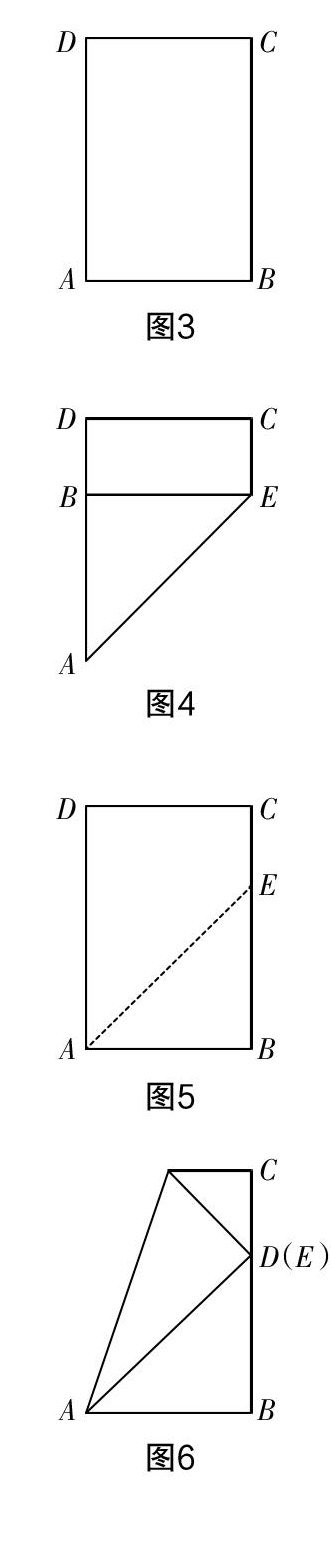
要证明一张普通A4纸的长短边之比为∶1,人们往往只能想到用直尺测量长与宽的长度并计算二者之比,这样做不仅麻烦,而且还会受到测量长度和计算过程中的误差影响. 除了通过测量计算的方法验证A组纸的长宽比为以外,还有一种轻松快速又有效的方法——数学折纸. 首先,将 A4 纸(图3)的短边AB翻折,使其与长边AD重合(图4),展开后(图5)由勾股定理可知折痕 AE=AB,用手按住点A运用旋转折纸法,可使点D与点E重合(图6),由此可直观形象地得出AD=AE=AB,即长边与短边之比为∶1.
思考正方形纸与白银长方形纸
的相互转化问题
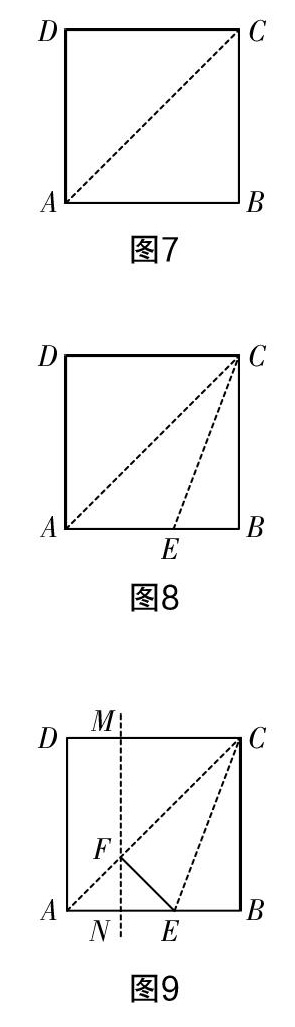
由一张白银长方形纸可以很容易通过折纸剪裁的方法得到一张正方形纸,那么,反过来,如何将一张正方形纸通过折纸剪裁的方法得到一张白银长方形纸呢?这就要找到正方形一条边上的分点,其实也很容易,可以进行如下操作. 首先,折出正方形ABCD的一条对角线AC,展开后(图7)由勾股定理可知折痕 AC=AB,然后折出∠ACB的平分线CE(图8),将正方形的一条边BC折到对角线AC上与之重合,将点B落在AC上的位置记为点F(图9),易知AC=CF,过此点折出正方形边AD的平行线MN,则BC=DC=MC,沿线NN将纸裁开,裁开后得到的长方形纸MNBC就是白银长方形纸.
两张A4纸折成立体嵌套三棱
锥造型
折纸是用一张纸折成各种不同形状的艺术活动. 一般来说,折纸作品必须完全由纸张折叠而成,在折纸的过程中不能使用剪刀或胶水,而在折纸的作品上也不需要多加任何色彩. 数学折纸活动是一种与数学紧密结合的活动,其与普通折纸的主要区别在于:不特别关注作品的艺术性,而重在揭示或诠释数学概念. 梁海声在《白银长方形:神奇的立体纸艺造型》一书中,用一张A4纸,不剪、不拼、不贴,通过简单的几次对折就折出了一个三棱锥. 首先将一张A4 纸长边对折一次成为A5纸张尺寸,再将长边对折一次成为A6纸张尺寸,这样原A4纸的4个顶角都折到右上角了,在没有纸张角的左上到右下正反折叠对角线,展开A4纸得到需要的 5 条折痕,围拢A4纸的四个角到一点上,就得到一个三棱锥,三棱锥的表面就是一张完整的A4纸. 做两个一样的四面体,相互错位嵌套起来,得到的双层四面体盒子更加牢固. 但是嵌套的四面体盒子无法自行闭合,还是要借助胶水黏合才行,这是因为所有的纸张都在表面,不具备拼插的条件.
两张正方形纸折成立体嵌套正
方体造型
受到这个双层四面体盒子的启发,笔者尝试教会学生用两张正方形纸做成一个双层嵌套的正方体盒子. 首先将一张正方形纸连续对折两次,这样原正方形纸张的4个顶角都折到右上角了,在没有纸张角的左上到右下正反折叠对角线,展开后将正方形纸的四个角都折到正方形的中心点上,得到面积为原来一半的小正方形,将小正方形的四条边按照对边分两次向中心点对折,展开正方形纸得到需要的折痕(图10). 以中心的小正方形为底面,将四个角立起来,中间多余的部分向内折,四个顶角围拢到一点上,就得到了一个正方体. 做两个一样的正方体,相互错位嵌套,并将中间多余的部分拼插起来,就得到一個牢固完整的双层正方体盒子(图11).
这个正方体盒子不仅制作简单,而且嵌套完美,能够自行闭合. 两张规则完整的正方形纸不粘、不剪,简单的错位嵌套后就能折成一个牢固完整的正方体造型,这个具有高度美感的立体构成让学生不禁感叹数学折纸的神奇魅力,对激发学生的数学学习兴趣具有积极的作用.

