例谈高中数学课堂中的“数学实验”
连信榕


伽利略的比萨斜塔自由落体实验,推翻了先贤亚里士多德的落体理论;牛顿的棱镜分解太阳光实验让我们看到了七色的阳光;卡文迪许的扭秤实验精确测量出了万有引力常数……,显然,物理学是依赖实验的科学,居里夫人经典的提取镭实验,门捷列夫的元素周期表都离不开化学实验,孟德尔更是从豌豆实验中发现了旷世的生物遗传律。
可以说物理、化学、生物都离不开实验,那么数学呢?数学需要实验吗?
答案是肯定的!数学需要实验!著名教育家G‘波利亚指出:“数学有两个侧面,一方面它是欧几里德式的严谨科学,从这个方面看,数学像是一门系统的演绎科学;但另一方面,创造过程中的数学,看起来却象一门试验性的归纳科学,”这里我们主要来谈谈第二个方面,笔者认为数学实验是指学生在教师的引导下,利用各种实验器材,包括图形计算器,数学软件等工具,动手实践,自主探索,从而发现规律,提出猜想,并验证猜想的过程,以下,通过几个案例谈谈数学实验的创设策略。
案例1直线与平面的垂直判定——有趣的折纸活动蕴含着数学定理
实验器材:三角形纸片、矩形纸片、半圆纸片各一张。
实验目的:通过翻折纸片让三种纸片立在桌面上,
问题设置:(1)这三种纸片都能通过翻折立在桌面上吗?
(2)翻折一次能做到吗?
(3)它们的折痕和桌面是什么关系?
(4)它们的折痕在各自纸片中有什么共同点?
(5)你能将这个实验转化为数学语言吗?
评析学生通过折三种类型的纸片归纳出线面垂直的判定定理:若一条直线垂直面内的两交线,则线面垂直,显然地,通过教师的有效创设,学生通过思考、操作、实验、归纳、猜想、修正,感受了知识的发生发展的过程,而学生亲历数学知识的建构过程,正体现了以学生为主体的课程理念,也符合学生的认知规律,
案例2糖水变甜了吗?——喝杯糖水让数学课与众不同
实验器材:一杯开水和若干糖,
实验目的:通过往开水中加糖并喝糖水提取数学解释,
问题设置:(1)往白开水中加一勺糖,味道会发生什么样的变化?
(2)继续往糖水中加一勺糖,味道与刚才相比发生怎样的变化?
(3)你能用数学语言解释这一变化吗?
(4)你能证明这个数学规律吗?
案例3幂函数图像的画法——数学软件带来的数学实验革命
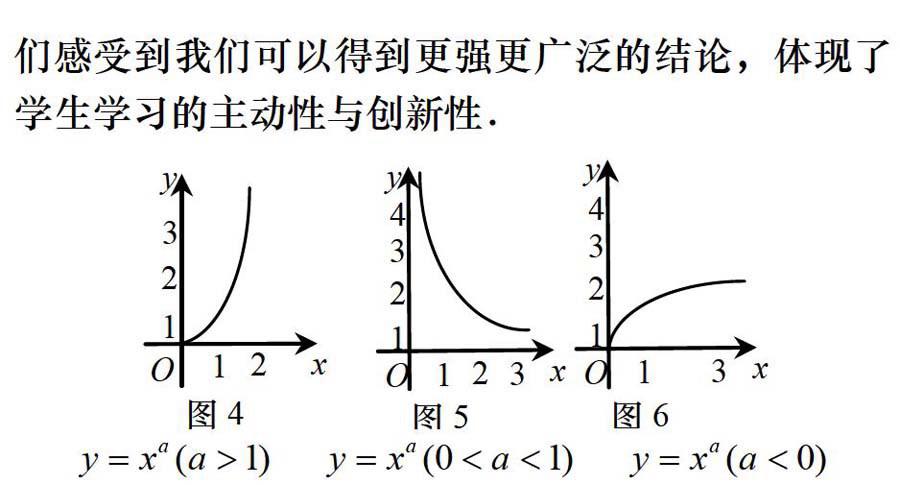
评析本案例中的函数图像对高中学生而言,无法通过传统的演绎推理得到,必须通过数学实验完成,而《超级画板》便为它提供了一个数学实验室,通过操作,学生惊讶地发现规律(如图4-6),再结合定义域和奇偶性即可得到任意的有理指数幂的幂函数图像画法,在该案例中,通过数学实验,让学生们感受到我们可以得到更强更广泛的结论,体现了学生学习的主动性与创新性。
案例4班级里会出现两位同学同年同月同日生吗?一调查实验推翻固有认知
实验器材:调查问卷
实验目的:探究班级(50人)中至少出现两位同学同年同月同日生的概率。
问题设置:(1)如果两个人同年同月同日生,是不是一件很神奇的事?
(2)这里的“神奇”二字,用数学解释是什么?
(3)我们班级有50名同学,认为会出现同年同月同日生的同学请举手。
(4)请同学A公布调查年级六个班的结果(课前安排)。
(5)调查结果是否推翻了你的固有认知呢?你能找到它的数学解释吗?案例5拍了几次手?一一游戏让数学更具亲和力实验器材:纸和笔(用于记录)。
实验目的:设计拍手游戏,通过游戏方式得到数学结论并加以证明。
问题设置:设置拍手游戏如下:5位同学(ABcDE)围坐一圈,A报数l,B报数l,c报数2,D报数3,……,此后按顺序每位同学报的数是前两位报数的总和,当报出的数字为3的倍数时,该同学拍手一次。
(1)统计拍手的情况,能发现规律吗?
(2)能将上述规律提炼出数学语言并证明吗?
(3)当报到100个数时,A同学一共拍了几次手?
(09年福建高考数学压轴题)
(4)能理性证明上述问题吗?
不可否认,教学是一项庞大的工程,方法技巧很多,而数学实验符合新时期教师和学生的需求,正成为教学技能中的重要一环,其实在发达国家,数学实验早已成为常见的教学形式甚至是教学内容,他们不仅有实验教材,还有专属的数学实验室,显然,我们在这方面还有很长的路要走,本文通过若干案例分析了操作性数学实验,思维性数学实验,计算机辅助性数学实验,验证性数学实验等各类数学实验的形式,不仅丰富了教师的教学形式,给相对枯燥的数学课堂带来了活动与生机;而且发展了学生的数学素养,创造性地解决了实际问题,
数学是科学之王,科学需要实验,数学更需要实验!



伽利略的比萨斜塔自由落体实验,推翻了先贤亚里士多德的落体理论;牛顿的棱镜分解太阳光实验让我们看到了七色的阳光;卡文迪许的扭秤实验精确测量出了万有引力常数……,显然,物理学是依赖实验的科学,居里夫人经典的提取镭实验,门捷列夫的元素周期表都离不开化学实验,孟德尔更是从豌豆实验中发现了旷世的生物遗传律。
可以说物理、化学、生物都离不开实验,那么数学呢?数学需要实验吗?
答案是肯定的!数学需要实验!著名教育家G‘波利亚指出:“数学有两个侧面,一方面它是欧几里德式的严谨科学,从这个方面看,数学像是一门系统的演绎科学;但另一方面,创造过程中的数学,看起来却象一门试验性的归纳科学,”这里我们主要来谈谈第二个方面,笔者认为数学实验是指学生在教师的引导下,利用各种实验器材,包括图形计算器,数学软件等工具,动手实践,自主探索,从而发现规律,提出猜想,并验证猜想的过程,以下,通过几个案例谈谈数学实验的创设策略。
案例1直线与平面的垂直判定——有趣的折纸活动蕴含着数学定理
实验器材:三角形纸片、矩形纸片、半圆纸片各一张。
实验目的:通过翻折纸片让三种纸片立在桌面上,
问题设置:(1)这三种纸片都能通过翻折立在桌面上吗?
(2)翻折一次能做到吗?
(3)它们的折痕和桌面是什么关系?
(4)它们的折痕在各自纸片中有什么共同点?
(5)你能将这个实验转化为数学语言吗?
评析学生通过折三种类型的纸片归纳出线面垂直的判定定理:若一条直线垂直面内的两交线,则线面垂直,显然地,通过教师的有效创设,学生通过思考、操作、实验、归纳、猜想、修正,感受了知识的发生发展的过程,而学生亲历数学知识的建构过程,正体现了以学生为主体的课程理念,也符合学生的认知规律,
案例2糖水变甜了吗?——喝杯糖水让数学课与众不同
实验器材:一杯开水和若干糖,
实验目的:通过往开水中加糖并喝糖水提取数学解释,
问题设置:(1)往白开水中加一勺糖,味道会发生什么样的变化?
(2)继续往糖水中加一勺糖,味道与刚才相比发生怎样的变化?
(3)你能用数学语言解释这一变化吗?
(4)你能证明这个数学规律吗?
案例3幂函数图像的画法——数学软件带来的数学实验革命
评析本案例中的函数图像对高中学生而言,无法通过传统的演绎推理得到,必须通过数学实验完成,而《超级画板》便为它提供了一个数学实验室,通过操作,学生惊讶地发现规律(如图4-6),再结合定义域和奇偶性即可得到任意的有理指数幂的幂函数图像画法,在该案例中,通过数学实验,让学生们感受到我们可以得到更强更广泛的结论,体现了学生学习的主动性与创新性。
案例4班级里会出现两位同学同年同月同日生吗?一调查实验推翻固有认知
实验器材:调查问卷
实验目的:探究班级(50人)中至少出现两位同学同年同月同日生的概率。
问题设置:(1)如果两个人同年同月同日生,是不是一件很神奇的事?
(2)这里的“神奇”二字,用数学解释是什么?
(3)我们班级有50名同学,认为会出现同年同月同日生的同学请举手。
(4)请同学A公布调查年级六个班的结果(课前安排)。
(5)调查结果是否推翻了你的固有认知呢?你能找到它的数学解释吗?案例5拍了几次手?一一游戏让数学更具亲和力实验器材:纸和笔(用于记录)。
实验目的:设计拍手游戏,通过游戏方式得到数学结论并加以证明。
问题设置:设置拍手游戏如下:5位同学(ABcDE)围坐一圈,A报数l,B报数l,c报数2,D报数3,……,此后按顺序每位同学报的数是前两位报数的总和,当报出的数字为3的倍数时,该同学拍手一次。
(1)统计拍手的情况,能发现规律吗?
(2)能将上述规律提炼出数学语言并证明吗?
(3)当报到100个数时,A同学一共拍了几次手?
(09年福建高考数学压轴题)
(4)能理性证明上述问题吗?
不可否认,教学是一项庞大的工程,方法技巧很多,而数学实验符合新时期教师和学生的需求,正成为教学技能中的重要一环,其实在发达国家,数学实验早已成为常见的教学形式甚至是教学内容,他们不仅有实验教材,还有专属的数学实验室,显然,我们在这方面还有很长的路要走,本文通过若干案例分析了操作性数学实验,思维性数学实验,计算机辅助性数学实验,验证性数学实验等各类数学实验的形式,不仅丰富了教师的教学形式,给相对枯燥的数学课堂带来了活动与生机;而且发展了学生的数学素养,创造性地解决了实际问题,
数学是科学之王,科学需要实验,数学更需要实验!

