浅谈对数学习困因及教学建议
王历权 党忠良


1.现象
对数及对数函数是高中数学中的重要知识,也是学生学习障碍很大的一块内容,本部分要求学生能理解对数的概念,并能够说明对数与指数的关系,要掌握对数式与指数式的相互转化和对数的运算性质,并能理解推导这些法则的依据和过程,要能较熟练地运用对数运算性质解决实践问题,加强数学应用意识的训练,提高解决应用问题的能力,
然而实际教学发现,学生掌握对数运算和对数函数的情况并不理想,一种常见现象是下面这些类型的题目不断训练、评讲、纠错、再练习,学生还是会出错甚至无法下手,个中原因值得深思,
首先,学生没有真正理解对数运算的含义,全新的对数运算符号log是学生理解对数的一大障碍,教学中甚至发现一段时间后还有学生认为log。x中符号log。与x是相乘的关系,数学的符号语言是对数学对象、数学运算、数学关系和推理过程等作出表述的一种语言,是数学思维的外显形式,体现了数学思维的特征,同时也简化了数学思维过程,对数运算符号精练准确地表达了对数运算的两大要素,高度浓缩的对数运算符号是学生学习数学的第一个拦路虎。
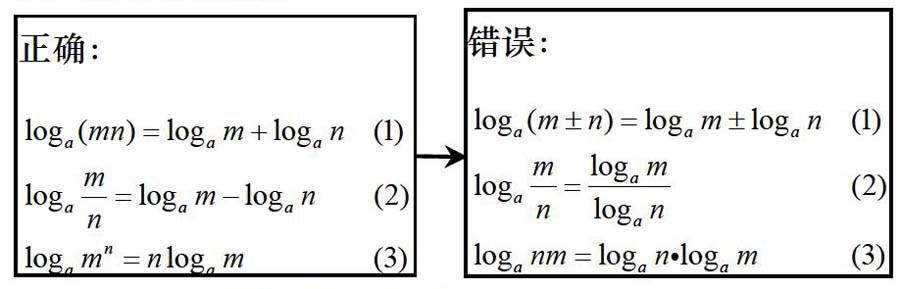
其次,对数运算法则容易混淆,学生未理解运算法则本质而死记公式,导致出错率高居不下,以下是常见的错误:
最后,灌输式教学剥夺了学生自主学习的权利,学生被动接受,没有在发现探索的过程中理解对数及对数运算,《普通高中数学新课程标准(实验2011)》(以下简称《课标》)要求理解对数的概念及其运算性质,知道用换底公式能将一般对数转化成自然对数或常用对数;通过阅读材料,了解对数的发现历史以及对简化运算的作用,通过具体实例,直观了解对数函数模型所刻画的数量关系,初步理解对数函数的概念,体会对数函数是一类重要的函数模型;能借助计算器或计算机画出具体对数函数的图像,探索并了解对数函数的单调性与特殊点,知道指数函数y=ax与对数函数y=logx互为反函数(a>0,a≠1)。
既如此,对数概念的教学应放在数学课堂的重要位置,教学中要创设问题情境,突出概念构建,让学生置身于发现对数概念的的过程中,以促进真正理解对数的概念和本质。
3教学建议
除针对易错问题辨误教学、特别强调真数必正、充分理解对数运算符号等方面狠下功夫外,笔者建议教学中还应从以下方面入手提升教学效率。
3.1对数发展史激发学习兴趣
16、17世纪之交,随着天文、航海、工程、贸易以及军事的发展,改进数字计算方法成了当务之急,苏格兰数学家纳皮尔(J,Napier,1550-1617)正是在研究天文学的过程中,为了简化其中的计算而发明了对数,对数的发明是数学史上的重大事件,天文学界更是以近乎狂喜的心情迎接这一发明,恩格斯曾经把对数的发明和解析几何的创始、微积分的建立称为17世纪数学的三大成就,
数学科学具有悠久历史,新课标要求在各个部分渗透数学史教学,以促使学生了解数学的本质和发展脉络,加深对数学概念、方法和思想的理解和认识,促使学生养成独立思考、积极探索的习惯,培养创造性思维和激发学习数学的兴趣和激情,
数学的三种形态密不可分,其中数历史形态的数学与教育形态的数学关系最为紧密,对中小学数学教师来讲,基于HPM(数学史与数学教育整合)的数学教育取向的数学史更具有实践性,一般来讲,数学史融入数学教学有显性的和隐性的两种基本形式,显性多指借用数学史料提高课堂趣味性,激发学生学习的激情;隐性融入是指根据历史对数学内容进行加工、裁剪、组织,用于学生学习或探究,
对数部分教学中,可以介绍适当对数发展历史或选择合适课题供学生探究,借助历史问题让学生充分领略和感受对数对简化运算的极大意义,同时通过了解前人为数学的发展所付出的心血,激励学生刻苦钻研,勇攀高峰。
3.2指数是对数的认知起点
历史上,对数的出现早于指数,但是学生学习对数需要以指数及指数运算作为认知的起点,教材中对数的概念是这样描述的:
如果ab=N(a>0且a≠1),那么b叫作以a为底,数N的对数,记作6=log。N
因此指对互化是促进学生理解对数的唯一有效途径,教学中应根据指数式和对数式之间的关系,引导学生通过指数幂的运算性质推导得出对数的运算性质,以加深对公式的理解和记忆,再利用指数式与对数式的关系完成证明,教学中教师应给足时间学生思考,以问题引导教学是学生真理解对数运算法则的保证,以下是某青年教师的教学片断,值得学习。
师:说的很好,以上三个等式即为要跟大家介绍的对数运算法则,
课堂实践表明,在预设的情景下学生完全可以从已有知识结构出发,在最近发展区内自主发现与构建,教师的任务则是提供教学素材、组织教学内容,我们要始终坚持这样一个观点:以尊重的态度,欣赏的眼光,学生是一定能在课堂上绽放出精彩的,
3.3螺旋上升,学以致用是关键
笔者在2015级高三下学期的一次模拟试题中选用了题目2,发现正确率很低,这表明在海量对数计算训练下,高三学生亦不能牢固掌握对数相应地运算公式,值得反思,教学中,不少老师给学生总结出两条有关对数问题的处理策略“一是底数不统一时先统一底数,二是对数求值时尽量将所有真数分解为质数”,不可谓不精练,也不可谓不适用,但大量学生依旧无奈,见对数问题就心虚。
笔者认为可以从以下两个方面入手,帮助学生摆脱困境。
首先,对数学习要循序渐进,螺旋上升,众所周知,初中介绍二次函数初步,学生进入高中后再深入学习二次函数相应的知识就容易多了,甚至很轻松,由此笔者认为对数教学内容的安排应在初高中通盘考虑,甚至可以在初中介绍整数幂的指数运算后增加相应的章节介绍对数的概念和运算法则初步,以确保学生消化吸收并理解对数的含义和本质,进入高中,将指数幂的运算由整数推广到实数后,再系统学习对数、对数运算法则和对数函数。
另外,现行《课标》中,函数概念与基本初等函数部分总共安排约32课时,这其中包含了函数概念与性质、指数及指数函数、对数及对数函数、幂函数、函数与方程、函数模型及应用等部分,一线教师都深知这是肯定不够的,要想让学生深刻理解对数概念和运算法则,需要较长时间才能办到,因此,适当拉长学习时间跨度是肯定有助于学生理解和掌握对数的。
其次,对数学习(包括其它任何知识)要学以致用,《课标》指出,数学是研究空间形式和数量关系的科学,是刻画自然规律和社会规律的科学语言和有效工具,数学科学是自然科学、技术科学等科学的基础,并在经济科学、社会科学、人文科学的发展中发挥越来越大的作用,
然而不幸的是,在高考指挥棒的影响下,大部分数学知识的应用被弱化甚至被无情地抛弃,导致学生认为学习数学的目的就是为了考试,对数是实用性很强的数学知识,来源于对现实世界的探索,也广泛应用于天文、考古等,对数教学中,教师应重视对数学知识的应用,利用碳14测定年代、铀核裂变等问题引出对数概念,选用学生喜闻乐见的兴趣材料,使学生在学习过程中感受到数学就在我们的周围,让学生在运用知识解决问题的过程中静心思考,促进理解。



1.现象
对数及对数函数是高中数学中的重要知识,也是学生学习障碍很大的一块内容,本部分要求学生能理解对数的概念,并能够说明对数与指数的关系,要掌握对数式与指数式的相互转化和对数的运算性质,并能理解推导这些法则的依据和过程,要能较熟练地运用对数运算性质解决实践问题,加强数学应用意识的训练,提高解决应用问题的能力,
然而实际教学发现,学生掌握对数运算和对数函数的情况并不理想,一种常见现象是下面这些类型的题目不断训练、评讲、纠错、再练习,学生还是会出错甚至无法下手,个中原因值得深思,
首先,学生没有真正理解对数运算的含义,全新的对数运算符号log是学生理解对数的一大障碍,教学中甚至发现一段时间后还有学生认为log。x中符号log。与x是相乘的关系,数学的符号语言是对数学对象、数学运算、数学关系和推理过程等作出表述的一种语言,是数学思维的外显形式,体现了数学思维的特征,同时也简化了数学思维过程,对数运算符号精练准确地表达了对数运算的两大要素,高度浓缩的对数运算符号是学生学习数学的第一个拦路虎。
其次,对数运算法则容易混淆,学生未理解运算法则本质而死记公式,导致出错率高居不下,以下是常见的错误:
最后,灌输式教学剥夺了学生自主学习的权利,学生被动接受,没有在发现探索的过程中理解对数及对数运算,《普通高中数学新课程标准(实验2011)》(以下简称《课标》)要求理解对数的概念及其运算性质,知道用换底公式能将一般对数转化成自然对数或常用对数;通过阅读材料,了解对数的发现历史以及对简化运算的作用,通过具体实例,直观了解对数函数模型所刻画的数量关系,初步理解对数函数的概念,体会对数函数是一类重要的函数模型;能借助计算器或计算机画出具体对数函数的图像,探索并了解对数函数的单调性与特殊点,知道指数函数y=ax与对数函数y=logx互为反函数(a>0,a≠1)。
既如此,对数概念的教学应放在数学课堂的重要位置,教学中要创设问题情境,突出概念构建,让学生置身于发现对数概念的的过程中,以促进真正理解对数的概念和本质。
3教学建议
除针对易错问题辨误教学、特别强调真数必正、充分理解对数运算符号等方面狠下功夫外,笔者建议教学中还应从以下方面入手提升教学效率。
3.1对数发展史激发学习兴趣
16、17世纪之交,随着天文、航海、工程、贸易以及军事的发展,改进数字计算方法成了当务之急,苏格兰数学家纳皮尔(J,Napier,1550-1617)正是在研究天文学的过程中,为了简化其中的计算而发明了对数,对数的发明是数学史上的重大事件,天文学界更是以近乎狂喜的心情迎接这一发明,恩格斯曾经把对数的发明和解析几何的创始、微积分的建立称为17世纪数学的三大成就,
数学科学具有悠久历史,新课标要求在各个部分渗透数学史教学,以促使学生了解数学的本质和发展脉络,加深对数学概念、方法和思想的理解和认识,促使学生养成独立思考、积极探索的习惯,培养创造性思维和激发学习数学的兴趣和激情,
数学的三种形态密不可分,其中数历史形态的数学与教育形态的数学关系最为紧密,对中小学数学教师来讲,基于HPM(数学史与数学教育整合)的数学教育取向的数学史更具有实践性,一般来讲,数学史融入数学教学有显性的和隐性的两种基本形式,显性多指借用数学史料提高课堂趣味性,激发学生学习的激情;隐性融入是指根据历史对数学内容进行加工、裁剪、组织,用于学生学习或探究,
对数部分教学中,可以介绍适当对数发展历史或选择合适课题供学生探究,借助历史问题让学生充分领略和感受对数对简化运算的极大意义,同时通过了解前人为数学的发展所付出的心血,激励学生刻苦钻研,勇攀高峰。
3.2指数是对数的认知起点
历史上,对数的出现早于指数,但是学生学习对数需要以指数及指数运算作为认知的起点,教材中对数的概念是这样描述的:
如果ab=N(a>0且a≠1),那么b叫作以a为底,数N的对数,记作6=log。N
因此指对互化是促进学生理解对数的唯一有效途径,教学中应根据指数式和对数式之间的关系,引导学生通过指数幂的运算性质推导得出对数的运算性质,以加深对公式的理解和记忆,再利用指数式与对数式的关系完成证明,教学中教师应给足时间学生思考,以问题引导教学是学生真理解对数运算法则的保证,以下是某青年教师的教学片断,值得学习。
师:说的很好,以上三个等式即为要跟大家介绍的对数运算法则,
课堂实践表明,在预设的情景下学生完全可以从已有知识结构出发,在最近发展区内自主发现与构建,教师的任务则是提供教学素材、组织教学内容,我们要始终坚持这样一个观点:以尊重的态度,欣赏的眼光,学生是一定能在课堂上绽放出精彩的,
3.3螺旋上升,学以致用是关键
笔者在2015级高三下学期的一次模拟试题中选用了题目2,发现正确率很低,这表明在海量对数计算训练下,高三学生亦不能牢固掌握对数相应地运算公式,值得反思,教学中,不少老师给学生总结出两条有关对数问题的处理策略“一是底数不统一时先统一底数,二是对数求值时尽量将所有真数分解为质数”,不可谓不精练,也不可谓不适用,但大量学生依旧无奈,见对数问题就心虚。
笔者认为可以从以下两个方面入手,帮助学生摆脱困境。
首先,对数学习要循序渐进,螺旋上升,众所周知,初中介绍二次函数初步,学生进入高中后再深入学习二次函数相应的知识就容易多了,甚至很轻松,由此笔者认为对数教学内容的安排应在初高中通盘考虑,甚至可以在初中介绍整数幂的指数运算后增加相应的章节介绍对数的概念和运算法则初步,以确保学生消化吸收并理解对数的含义和本质,进入高中,将指数幂的运算由整数推广到实数后,再系统学习对数、对数运算法则和对数函数。
另外,现行《课标》中,函数概念与基本初等函数部分总共安排约32课时,这其中包含了函数概念与性质、指数及指数函数、对数及对数函数、幂函数、函数与方程、函数模型及应用等部分,一线教师都深知这是肯定不够的,要想让学生深刻理解对数概念和运算法则,需要较长时间才能办到,因此,适当拉长学习时间跨度是肯定有助于学生理解和掌握对数的。
其次,对数学习(包括其它任何知识)要学以致用,《课标》指出,数学是研究空间形式和数量关系的科学,是刻画自然规律和社会规律的科学语言和有效工具,数学科学是自然科学、技术科学等科学的基础,并在经济科学、社会科学、人文科学的发展中发挥越来越大的作用,
然而不幸的是,在高考指挥棒的影响下,大部分数学知识的应用被弱化甚至被无情地抛弃,导致学生认为学习数学的目的就是为了考试,对数是实用性很强的数学知识,来源于对现实世界的探索,也广泛应用于天文、考古等,对数教学中,教师应重视对数学知识的应用,利用碳14测定年代、铀核裂变等问题引出对数概念,选用学生喜闻乐见的兴趣材料,使学生在学习过程中感受到数学就在我们的周围,让学生在运用知识解决问题的过程中静心思考,促进理解。

