再谈六角幻方
黄剑潮
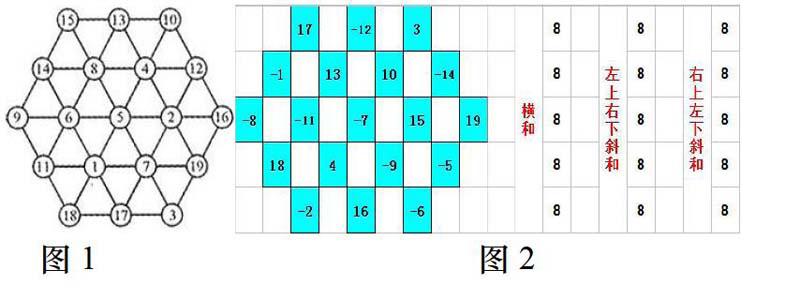
英国一位名叫阿当斯的数学爱好者,从1910年至1962年共花了52年心血终将六角幻方排列成功,得到了横的5行及斜的10行上各自数字之和都是38的六角幻方(图1).
若将1-19这19个数放入图1的19个小圆圈中,所有的可能性显然有19!种之多.
现在换一种思路,若将绝对值是1-19的19个数,也就是可选用的数分别为±1,±2,……,±18,±19时,那么这5横行及10斜行上的各自数字之和就不仅仅只有38了,可以想象这种情形下的填入数字的可能性比前者大2倍,难度也将随之增大. 在此提供一种5横行及10斜行上的各自数字的和为8的一种解(图2),以飨读者.

英国一位名叫阿当斯的数学爱好者,从1910年至1962年共花了52年心血终将六角幻方排列成功,得到了横的5行及斜的10行上各自数字之和都是38的六角幻方(图1).
若将1-19这19个数放入图1的19个小圆圈中,所有的可能性显然有19!种之多.
现在换一种思路,若将绝对值是1-19的19个数,也就是可选用的数分别为±1,±2,……,±18,±19时,那么这5横行及10斜行上的各自数字之和就不仅仅只有38了,可以想象这种情形下的填入数字的可能性比前者大2倍,难度也将随之增大. 在此提供一种5横行及10斜行上的各自数字的和为8的一种解(图2),以飨读者.

