“动起来”,实现变教为学的新举措
季金莉

[摘? 要] 生本课堂,就要真正激活学生在课堂活动中的主体性和思维性,而主动性和思维性的达成需要教师结合教学内容,真正让学生“动起来”,课堂将变教为学,变传授变探索.
[关键词] 主动学习;思维;课堂教学;变教为学
在提倡变教为学的新课改背景下,学生学习的主动性成为教师教学的关注点,将传统教学中教师的“教”转变成新型课堂中学生的“学”,打造高效课堂是师生共同的夙愿. 课改在我国已实施多年,在全国各地不断推陈出新的课程研发中,笔者学习了很多,也收获了很多. 经过多年的教学实践及反思,笔者意识到,在不断演变的课程教学中,教学形式不断发生着改变,但有一个原则始终没有发生改变,那就是让学生“动起来”,变被动接受为主动学习,成为课堂的主宰者. 下面笔者结合“2.5 等腰三角形的轴对称性(1)”(苏科版八年级上册)的教学片段来谈谈动手操作在初中数学中的重要作用.
引入环节:引起無意注意,激发学习兴趣
新授课通常由引入开始,引入环节的教学效果会直接影响学生对本节课的兴趣,因此如何引入是教师在教学设计时需仔细斟酌的. 高效的引入环节并不需要太丰富的形式,而是能够让学生动起来,激发学生的学习兴趣、增强学好本节课内容的信心.
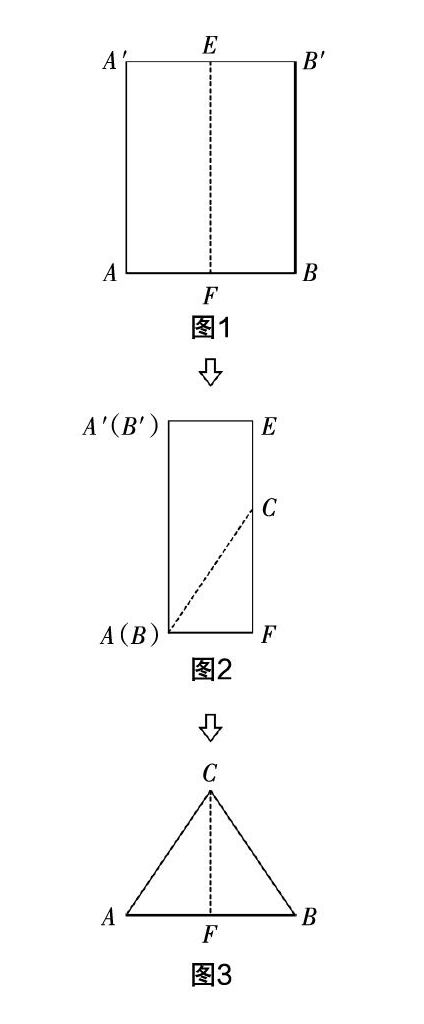
任务一:拿出一张A4纸ABA′B′(如图1),将它沿中线EF对折(如图2),在对折后的边EF上取一点C,连接CA(CB)并沿此线剪开,然后打开所得到的图形(如图3).
(完成方式:学生自主完成)
师:你得到了什么图形?
学生的回答参差不齐,有回答“三角形”,有回答“等腰三角形”,随即又统一了答案,一致认为是“等腰三角形”,教师肯定学生的回答之后板书课题.
师:大家在现实生活中见过哪些是等腰三角形的物体呢?
生1:屋顶的侧面.
生2:金字塔.
生3:三角铁.
……
设计意图? 学生在七年级已经认识了等腰三角形,知道了等腰三角形的概念,以简单的裁剪问题引入教学,可以较大限度吸引学生的注意力,让学生感受到本节课的内容并不难. 本节课的重要内容是等腰三角形的性质,而对称性是探索其性质的主线. 通过这样一个动手操作的过程可以让学生直观感受到对称的存在性,为接下来的探究提供充分的条件.
探究环节:优化教学过程,构建知识体系
在传统的教学过程中,该环节就是让学生观察猜想、证明性质,教学过程以教师为主导,学生的主体性得不到体现. 以学生的学为主的新型课堂就是要改变这种方式,通过让学生动手操作,自己构建知识体系.
任务二:将手中的等腰三角形沿着CF反复折叠,分别从线段、角、图形的角度观察它,结合前几节课的知识,你能得出什么结论?
(完成方式:小组合作,各自发表见解,组员相互补充,组长汇总整理,小组代表交流展示)
展示片段:
组一:我们小组观察后发现在这个图形中有相等的线段CA与CB,FA与FB;相等的角有∠A与∠B,∠ACF与∠BCF,∠CFA与∠CFB.
组二:我们小组还发现了△CAF与△CBF全等.
组三:我们小组还发现了这个图形沿着CF折叠能够完全重合,因此CF是它的一条对称轴,这个三角形是一个轴对称图形.
……
师:同学们观察得真仔细,上述结论中有些是我们通过等腰三角形的概念就能得出的,有一部分却是大家最新发现的.
师:我们知道,有两条边相等的三角形是等腰三角形,通过折叠得出的∠A=∠B是我们的新发现,可以将它概括为“等腰三角形的两个底角相等(简写成‘等边对等角)”,这是等腰三角形的第一个性质.
教师板书“性质1”及其几何表示.
师:刚才组三得出了等腰三角形是轴对称图形的结论,那么它有几条对称轴呢?它的对称轴是什么呢?
生1:它只有一条对称轴,就是CF.
生2(补充):一般的等腰三角形都只有一条对称轴,但是特殊的等腰三角形——等边三角形有三条对称轴.
师(追问):你学会了由一般到特殊的思考问题的方法,非常棒!那能否更具体一点告诉大家,一般等腰三角形的对称轴是哪一条线段呢?
生2:是底边上的高.
师(追问):你如何知道它就是底边上的高线?
生2:以图3为例,由全等可知∠CFA与∠CFB相等,它们本身互为邻补角,因此这两个角都为直角,即CF是AB边上的高.
生3:我觉得这条线也是等腰三角形的顶角平分线,也是根据△ACF与△BCF全等证出.
生4:同样根据全等还可以证出CF是底边的中线.
师:这是一个了不起的发现,等腰三角形的顶角平分线、底边上的中线、底边上的高线相互重合.
教师随即板书等腰三角形的“性质2”及其几何表示方法.
设计意图? 性质的推导及证明环节是教学的中心环节,在这个环节中,让学生通过动手操作,发现零碎的小结论,找到自身的“存在感”,然后教师引导学生一起将零碎的结论进行整合与归纳,形成新知识. 这个过程的主体是学生,学生通过动手操作发现与构建了新知,所有的知识都是自然生成的,教师只是一个辅助者.
运用环节:体会数学运用,促进新知内化
运用就是上一环节归纳所得的性质的运用,通常以例题及练习题的形式呈现. 在这个环节中的动手操作主要体现在问题的解决上,让学生自己体会问题解决的过程,找到问题解决的思路,才能促进新知的内化. 在这个过程中,学生依旧是主体.
例1? 如图4,在△ABC中,CA=CB,点D在BC上,且CD=AD=AB,求△ABC各角的度数.
(完成方式:学生独立完成后小组相互纠错改正,组内解决问题)
例1变式? 如图5,在△ABC中,AB=AC,点D在BC上,且AD=BD,找出图中相等的角并说明理由.
(完成方式:学生独立思考后全班展示,共同探讨)
例2如图6,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
求证:BE=CE.
(完成方式:学生独立完成后小组交流,组长汇总不同方法,全班交流展示)
例2变式? 如图7,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°,原题设其他条件不变. 求证:△AEF≌△BCF.
(完成方式:学生独立完成后全班交流展示,师生共同探讨解决问题)
展示片段(由于篇幅限制,本文仅展示例1变式的师生交流过程):
生1:在△ABC中,根据等边对等角,因为AB=AC,所以∠B=∠C,因为AD=BD,所以∠B=∠BAD,由已知得∠B=∠C,所以∠C=∠BAD.
師:你的领悟能力很强,学会了将所学知识进行实际运用,回答得很有条理,那么还有没有其他相等的角呢?
生1迟疑……
师:刚才你把三角形的所有内角全部比较了一遍,得到了所有相等的内角. 请你仔细观察,图中除了内角,还有什么样的角呢?
生1:还有外角.
师:反应真快,哪一个角是外角?是谁的外角呢?
生1:∠ADB是一个外角,它是△ACD的外角.
师(追问):所以根据外角的定义,它是哪两个角之和?
生1:∠ADB=∠CAD+∠C.
师:结合刚才的结论,你是否有新的发现?
生1(豁然开朗):由∠C=∠BAD可知∠CAD+∠C=∠CAD+∠ABD,所以∠ADB=∠BAC.
师:很好,你通过自己的努力完善了思考过程,得到了这个问题的完整答案,这种态度值得同学们学习.
设计意图? 本环节设置了两个例题及两个变式,两个例题是对性质的简单运用,学生自己解决基本无压力,因此可以让学生在小组内自行解决,教师绝不代替. 对于难度稍高的变式,先给学生足够的时间来动手操作,组内互助,教师只在学生无法独立解决的时候才提供引导,但是主要过程还是由学生完成,教师决不剥夺学生动手的机会.
总结环节:渗透数学思想,培养学习习惯
总结环节是课堂教学的最后环节,在以学生主动学习为主的课堂中,该环节绝不是以简单的一言两语来概括,而是渗透数学思想、总结数学方法,培养学生总结反思能力的过程.
1. 本节课学了哪些内容?
2. 本节课你领悟到了哪些数学思想?
3. 你这节课的最大收获是什么?
4. 你在这节课中“捕获”了哪些易错点和注意点?
5. 你对这节课还有什么疑惑吗?
6. 你觉得下一节课应该学习什么内容?
(完成方式:学生各抒己见,畅所欲言)
展示片段:
生1:我这节课学到了等腰三角形的两条重要性质,知道了这两条性质实质是由它的轴对称性得到的. 我觉得最应该注意的就是在解决相关几何问题时要找准、找全题目中的条件.
生2:这节课我领悟到了方程思想、转化思想及数形结合思想,例2变式我还不是太明白,课后我会找同学给我讲解的.
生3:我这节课最大的收获就是自己推导出了“三线合一”的证明方法,这让我对学好数学更加有信心了.
生4:按照从一般到特殊的推理方法,下一节课应该学习“等边三角形的轴对称性”.
……
设计意图? 总结并不是一节课的完结,而是一节课的升华,也是下一节课的开始,更是知识的不断延续. 这个环节的问题可以是预设的也可以是随机提出的,以开放性问题的方式让学生通过对自己的审视达到对课堂的小结,在这个过程中,生生与师生间毫无戒备的对话便是学生“动起来”的体现.
新课改是一场改变教学理念的革命,是由教师的灌输式教学变成学生主动获取知识的革命. 在这场革命中,数学作为一门朴实的学科,并不需要以太多“花样”来引起初中学生的注意,而是要通过数学的实用价值让学生感到数学有用而主动去学. 让学生“动起来”就是要将课堂的主动权交给学生,让学生体会到数学的价值和解决问题的成就感,进而学会学习,真正实现“变教为学”.

