类比“等差数列”探究“等比数列”
王耀文


新的课程标准倡导积极主动、勇于探索的学习方式,鼓励学生在学习过程中,养成独立思考、积极探索的习惯,在学习数学时,注重经历观察发现、归纳类比的思维过程,下面就在学生已经学习了等差数列所有内容的前提下,如何引导学生类比已学等差数列的知识和研究等比数列的方法探究“等比数列”谈谈自己的想法,敬请各位同仁提出宝贵意见,
1.复习回顾(意在进一步掌握等差数列的相关知识,为学习等比数列做铺垫)
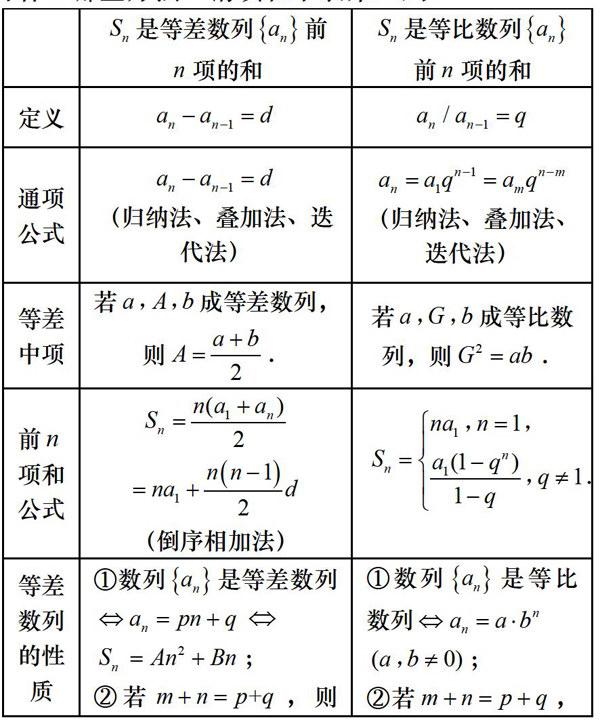
教师:在等差数列的学习中,我们学习了哪些内容?哪些方法?请填在下表第二列,
2.新课引入(意在引导学生类比联想,通过探讨发现特殊数列除了等差数列外,还应有等和数列、等积数列、等比数列)
教师:等差数列是指后项与前一项的差的运算,能否将差的运算替换为其它运算呢?请同学们思考,这样的数列是否存在,若存在,请举出具体的例子,5分钟后,
学生l:若一个数列从第二项起,每一项与前一项的和都等于同一个常数,则这个数列是否可称为等和数列,这个常数称为公和,这种数列很简单,比如首项为l,公和为3的等和数列为:1,4,1,4,1,4,......它的通项公式及前n项和公式都比较简单,
学生2:若一个数列从第二项起,每一项与前一项的积都等于同一个常数,则这个数列是否可称为等积数列,这个常数称为公积,这种数列也很简单,比如首项为l,公积为3的等积数列为:1,3,1,3,1,3,…,它的通项公式及前n和公式也都比较简单,
学生3:若一个数列从第二项起,每一项与前一项的商(或比)都等于同一个常数,则这个数列是否可称为等商(比)数列,这个常数称为公商(比),这种数列有点类似等差数列,但又不同,比如由定义,在等比数列中任意一项都不为0且公比也不为0,
笔者肯定了学生的想法,并指出:由于等和数列和等积数列比较简单,我们很容易利用定义根据它的首项、公和(或公积)给出它的通项公式和前”项和公式,因此教材中没有涉及,但在一些考卷中出现过,主要考查考生们的阅读理解能力和数学能力,从刚才同学们的回答我们已经解决了这两类数列的基本问题,而等比数列和等差数列很类似,但又有区别,下面我们类比等差数列的研究方法来学习研究等比数列,
3.新课探究(意在放手学生,让他们大胆猜想、探索)
教师:请同学们独立思考,类比第2列填写上表的第3列,要求先填写自己能独立解决的问题,然后以小组为单位,交流、思考、补充,
临近下课时,经过学生的共同努力,完成了除前”项和公式外的所有内容(见表格),教师表扬了同学们,并要求学生课后试着推导等比数列前”项和公式(要求如果直接讨论有难度的话,可以先讨论:
这3个练习的目的是:(1)判断是否为等比数列;(2)如果是等比数列,公比是否为l;(3)满足等比数列求和公式时,一定要注意求多少项的和;(4)独立思考:一个数列有等比数列的背景时,求和是否可考虑错位相减法;(5)理解错位相减法:步骤:列式、错位、相减,“错位”的目的是对其同类项,是为了后面计算不错,
4.课后反思
显然,这样的设计是在明确目标的前提下,学生在已有等差数列知识和研究方法的基础上进行的自主探究,学生研究的热情比较高涨,而且从作业反馈的信息来看,效果也比较好,因此,教师在教学中一定要树立“以人为本”的理念,相信学生,放手使他们大胆探究,



新的课程标准倡导积极主动、勇于探索的学习方式,鼓励学生在学习过程中,养成独立思考、积极探索的习惯,在学习数学时,注重经历观察发现、归纳类比的思维过程,下面就在学生已经学习了等差数列所有内容的前提下,如何引导学生类比已学等差数列的知识和研究等比数列的方法探究“等比数列”谈谈自己的想法,敬请各位同仁提出宝贵意见,
1.复习回顾(意在进一步掌握等差数列的相关知识,为学习等比数列做铺垫)
教师:在等差数列的学习中,我们学习了哪些内容?哪些方法?请填在下表第二列,
2.新课引入(意在引导学生类比联想,通过探讨发现特殊数列除了等差数列外,还应有等和数列、等积数列、等比数列)
教师:等差数列是指后项与前一项的差的运算,能否将差的运算替换为其它运算呢?请同学们思考,这样的数列是否存在,若存在,请举出具体的例子,5分钟后,
学生l:若一个数列从第二项起,每一项与前一项的和都等于同一个常数,则这个数列是否可称为等和数列,这个常数称为公和,这种数列很简单,比如首项为l,公和为3的等和数列为:1,4,1,4,1,4,......它的通项公式及前n项和公式都比较简单,
学生2:若一个数列从第二项起,每一项与前一项的积都等于同一个常数,则这个数列是否可称为等积数列,这个常数称为公积,这种数列也很简单,比如首项为l,公积为3的等积数列为:1,3,1,3,1,3,…,它的通项公式及前n和公式也都比较简单,
学生3:若一个数列从第二项起,每一项与前一项的商(或比)都等于同一个常数,则这个数列是否可称为等商(比)数列,这个常数称为公商(比),这种数列有点类似等差数列,但又不同,比如由定义,在等比数列中任意一项都不为0且公比也不为0,
笔者肯定了学生的想法,并指出:由于等和数列和等积数列比较简单,我们很容易利用定义根据它的首项、公和(或公积)给出它的通项公式和前”项和公式,因此教材中没有涉及,但在一些考卷中出现过,主要考查考生们的阅读理解能力和数学能力,从刚才同学们的回答我们已经解决了这两类数列的基本问题,而等比数列和等差数列很类似,但又有区别,下面我们类比等差数列的研究方法来学习研究等比数列,
3.新课探究(意在放手学生,让他们大胆猜想、探索)
教师:请同学们独立思考,类比第2列填写上表的第3列,要求先填写自己能独立解决的问题,然后以小组为单位,交流、思考、补充,
临近下课时,经过学生的共同努力,完成了除前”项和公式外的所有内容(见表格),教师表扬了同学们,并要求学生课后试着推导等比数列前”项和公式(要求如果直接讨论有难度的话,可以先讨论:
这3个练习的目的是:(1)判断是否为等比数列;(2)如果是等比数列,公比是否为l;(3)满足等比数列求和公式时,一定要注意求多少项的和;(4)独立思考:一个数列有等比数列的背景时,求和是否可考虑错位相减法;(5)理解错位相减法:步骤:列式、错位、相减,“错位”的目的是对其同类项,是为了后面计算不错,
4.课后反思
显然,这样的设计是在明确目标的前提下,学生在已有等差数列知识和研究方法的基础上进行的自主探究,学生研究的热情比较高涨,而且从作业反馈的信息来看,效果也比较好,因此,教师在教学中一定要树立“以人为本”的理念,相信学生,放手使他们大胆探究,

