培养直觉思维能力,拓展解题视野
刘雪梅

[摘? 要] 文章结合教学案例,引导学生从整体上观察和研究对象,鼓励学生提出近似合理的猜想,数形兼顾、相辅相成,让学生取得应用知识解决问题的经验等,从而让学生拓展思路、提升视野,提高解题速度和解题质量.
[关键词] 课堂教学;直觉思维;解题视野;创造性
直觉思维是一种直观、直接的思维,它是指未经过仔细的推敲和逐步的分析,就能直接揭示事物的本质的思维方式,它从事物的总体出发把握研究对象,对问题的实质进行快速判断,大胆地提出一些合理的推测和猜想,其中包括某些顿悟和灵感. 它具有敏捷性、独立性、跳跃性、试探性和简洁性等特点. 在课堂教学中,鼓励学生认真观察、合理想象、大胆猜测,就会防止学生机械地思考问题,从而提升直觉思维能力,促进逻辑思维的发展. 那么怎样才能达成以上目标呢?笔者从几个方面进行诠释.
引导学生从整体上观察和研究对象
直觉思维要求直接从整体上去研究和把握对象,通过直接的观察,快速缩小问题的突破口,捕捉到解决问题的契机.
案例1小明和小强从同一地点出发去电影院,小明要走40分钟,小强要走30分钟,如果小明先走5分钟,小强再出发,问小强要走几分钟才能追上小明?
这是初中阶段常见的行程类应用题. 见到这类问题,大部分师生第一反应就是用“方程的思想”予以解决. 一般的解题方案是:
设小强要走x分钟才能追上小明. 根据题意列方程,得x=(x+5),解得x=15.
如果长期以单一方式解决问题,就必然会限制学生的思维发展,使他们解决问题时带有局限性. 我们可以尝试换个角度,引导学生从整体上观察问题,直接触及问题的实质. 不难看出:这段路程小明要走40分钟,小强要走30分钟,而小明先走5分钟,就必定比小强晚到5分钟. 那么我们就可以得到,小强追上小明的时间应是小强行至全程的中点时,故列式为:x=30÷2=15.
显然,换个角度解决问题,既拓宽了学生的解题思路,又使数学充满趣味.
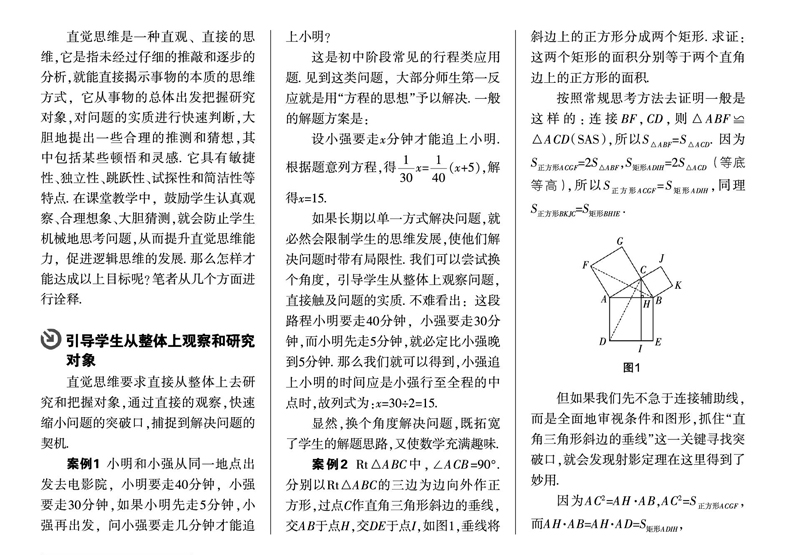
案例2Rt△ABC中,∠ACB=90°. 分别以Rt△ABC的三边为边向外作正方形,过点C作直角三角形斜边的垂线,交AB于点H,交DE于点I,如图1,垂线将斜边上的正方形分成两个矩形. 求证:这两个矩形的面积分别等于两个直角边上的正方形的面积.
按照常规思考方法去证明一般是这样的:连接BF,CD,则△ABF≌△ACD(SAS),所以S=S. 因为S=2S,S=2S(等底等高),所以S=S,同理S=S .
但如果我们先不急于连接辅助线,而是全面地审视条件和图形,抓住“直角三角形斜边的垂线”这一关键寻找突破口,就会发现射影定理在这里得到了妙用.
因為AC2=AH·AB,AC2=S,而AH·AB=AH·AD=S,
所以S=S,同理,S=S .
鼓励学生提出近似合理的猜想
估测、尝试和猜想是直觉思维的显著特征之一,从古至今,很多伟大的发现都源于大胆的猜想. 数学教学中常常可以让学生抓住某些显著的特征,通过大胆的猜想得到结论,然后再去验证结论的正确性.
案例3已知:如图2,在梯形ABCD中,AD∥BC,点E是AB的中点,过点E作EF⊥CD于点F,EF=4.5 cm,CD=8 cm,求梯形ABCD的面积.
本题乍看起来显然无从下手. 因为“S=(AD+BC)·高”,而没有一个已知条件与之相关. 这时,如果教师鼓励学生认真观察、大胆猜测,就会发现,EF是CD边上的高,而高往往与面积有关,它的结果会不会是“8×4.5”,也就是“底×高”呢?
分析? 若此题的结果是“8×4.5”,即“底×高”,而“S=底×高”,则CD应该是平行四边形的底,EF应该是它的高. 那么,我们可以构造出一个平行四边形吗?于是过点E作CD的平行线,再通过两个三角形全等将梯形面积转化为平行四边形的面积,求得梯形的面积为36. 猜想结果正确.
由此看来,猜想确实有其重要的作用. 在数学教学中,教师要引导、鼓励学生先去大胆猜想,猜结论、猜方法、猜定理,然后通过严谨的、系统的方法进行论证.
数形兼顾,相辅相成
数形结合是探索解决数学问题的重要途径,它对提高学生的直观思维能力、综合运用能力,培养学生的数学素养都起着十分重要的作用.
1. 以形助数,直观明快
图形的直观性不言而喻. 在教学中,教师要有意识地引导启发学生挖掘形与数之间的关系,促使问题向直观形象转化,进而沟通知识与知识之间、方法与方法之间的联系,并从中发现新的解题思路,得到更好的解题方法,达成举一反三、触类旁通的教学目标. 这是一件多么了不起的事情.
案例4解方程x-4-x+2=2.
常规的解法是划分三个区间进行分类讨论,去绝对值符号求解. 解法如下:①当x≤-2时,4-x+x+2=2,得到6=2,矛盾,无解;②当-2
如果我们联想到绝对值的几何意义,就会发现,方程的解是数轴上这样的一个点:它与x=4的距离比与x=-2的距离大2,容易得到此点是x=0. 如图3.
这样的例子还有很多. 有时借助图形或几何意义来表示数量关系,能更直观地确定参数的位置,从而避免烦琐的分类讨论和计算. 不仅使问题更简洁直观,同时还拓展了学生的解题视野.
2. 数赋形意,直击要害
把具有一定关系的数量与图形联系起来,就会使抽象的概念和复杂的数量关系得到整合,从而降低题目的难度,找到解题思路. 许多数式往往有着几何背景,我们要善于根据问题的结构特征,联想到有关的几何意义及其图形,进而巧妙地解决问题.
案例5如图4,在?ABCD中,∠ABC=60°,AB=,AD=2,点E在AD上(点E不与点A,D重合). 过点E作EF⊥BC且交DC的延长线于点F,连接BF. 在线段DF上是否存在一点H,使得四边形ABFH是菱形?如果存在,请说明点E、点H分别在线段AD,DF上什么位置时四边形ABFH是菱形,并证明;如果不存在,请说明理由.
本题如果单纯地从找点E和点H的位置出发很难找到突破口,但是如果关注到“∠ABC=60°,AB=,AD=2”这一组条件,就会马上联想到这恰好是一个锐角为30°的直角三角形的一条直角边和斜边的长,进而想到过点A作AH⊥DF于点H (如图5),从而解决问题.
数形结合是一种需要扎实的基础知识作为支撑的思想方法,应用的关键在于联系转化. 根据数量关系找到几何图形的结构特征,使问题变得简单、直观. 所以,在教学中应注意挖掘和渗透. 只有把思想方法贯彻始终,才会不断地提高学生对所学知识融会贯通的能力,培养学生思维的目的性和组织性.
让学生取得应用知识解决问题的经验
直觉思维很大程度上产生于经验,它是在观察、归纳、类比和联想的基础上,有时以“顿悟”的形式出现,即通常所说的产生了“灵感”. 实际上它是认知过程中的一种飞跃. 有时候我们解一道数学问题,会有一个百思不得其解的过程,然后在某一个点上忽然出现某种联想而豁然开朗,找到了解决的方法或猜到了一条证明的途径. 可见,“灵感”的产生、“顿悟”的出现并非凭空而来,而是需要雄厚的知识储备、丰富的实践经验以及不断总结、归纳、提升. 教师要让学生懂得:灵感基于经验的转换(如比较、类比、推广、相似变换、数形结合等),而经验的转化基于牢固的基础知识,学会应用知识去解决问题,并不断总结这方面的经验,就会提高自己的直觉思维能力,从而拓展解题视野的宽度.
以上讨论了直觉思维的意义以及直觉思维能力的培养,强调了直觉思维的地位和作用,但这并不意味着可以忽略或减弱逻辑思维能力的培养. 从上面的论述中可以看出,只有把直觉思维和逻辑思维有机地结合起来,才能有效地发展学生的创造性思维,从而促使学生进行多维思考,最大限度地发挥数学课堂的育人价值.

