以探究为导向，构筑灵动、高效的课堂

    张超

    

    

    

    [摘? 要] 文章重点探究了一次函数的表达式与图像之间的一一对应关系. 教学活动中让学生经历了“操作—猜想—探究—验证”的过程，利用“描点法”绘制一次函数的图像，引发了学生对“两点法”刻画一次函数图像的思考.

    [关键词] 表达式;直线;一一对应

    对教学目标以及所处教材体系的研究

    苏科版《义务教育课程标准试验教科书·数学》（八年级上册第6章6.5节）“一次函数图像（第1课时）”是在学习了一次函数的概念、三种函数不同表示方法的基础上，让学生感受、探究一次函数的图像，掌握用“描点法”来画一次函数的图像. 一次函数的图像作为第一个函数图形的研究，具有代表性. 结合课标，笔者对这节课教学目标的理解是：（1）一次函数的图像是怎么形成的;（2）一次函数的图像为什么是一条直线;（3）如何描绘出一次函数的图像.

    关于教学过程的研究

    1. 情境引入

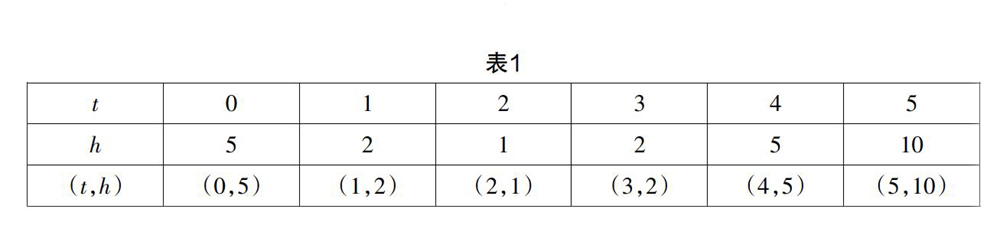
    在太阳和月球引力的作用下，海水定时涨落的现象称为海洋的潮汐，涨落的水位高低称为潮位. 随着时间t的变化，潮水的高度h也随之发生变化. 假设海洋潮水高度h与时间t之间满足这样的函数关系式：

    h=（t-2）2+1（0≤t≤5）.

    问题1：你还有哪些不同的方法来表示h与t之间的函数关系？

    问题2：表1中的两个变量t，h的数值如何确定？

    问题3：如何描绘该函数的图像？

    课堂回放 问题1回顾函数的三种不同表示方法;问题2引导学生通过t和h这两个变量数值的对应，刻画它们的函数关系;问题3利用直角坐标系把函数图像问题转化成点的坐标问题.

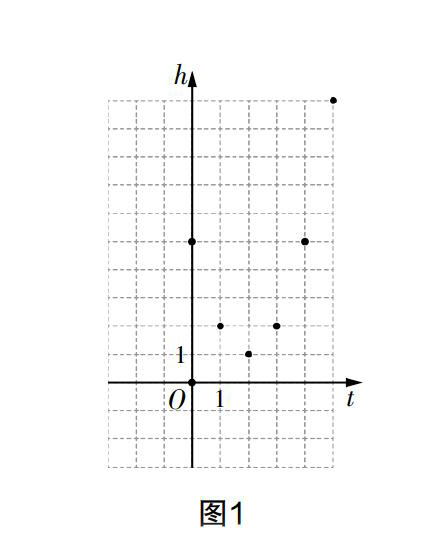
    学生活动1 在平面直角坐标系中描绘出表1中关于两个变量所形成的点.

    课堂回放 师：函数图像就是图1中孤立的6个点吗？说说你的见解.

    生1：自变量t的取值范围是0≤t≤5，t的取值除了整数外还可以取小数.

    （学生动手尝试自变量t是小数的点）

    生2：函数的图像中存在无数个点.

    生3：（展示）无数个这样的点“靠在一起”就形成了一条曲线（如图2）.

    （部分学生展开讨论，表示质疑）

    师：好，希望通过本节课的探究能帮助大家验证猜想.

    师：把一个函数的自变量x的值与函数y的对应值分别作为点的横坐标和纵坐标，在直角坐标系中描出它的对应点，所有这些点组成的图形叫这个函数的图像.

    师：回顾刚才画函数图像的过程，我们经历了怎样的步骤？

    生（齐）：列表、描点、连线.

    设计构想? 引入生活实例，体现数学源于生活. 通过对函数三种表示方法的认识，了解不同表示方法的联系，为用描点法画函数图像做铺垫. 选择抛物线引入，目的是让学生不陷入函数图像是一条直线的定式中，也让学生思考一次函数的图像是否会像抛物线一样是弯曲的.

    2. 合作探究：一次函数y=2x+1的图像及画法

    （1）小组合作，师生交流探究过程

    师：列表应注意以下几点.

    ①通常，我们所选取的点应具有完备性，x的值取正数、0、负数.

    ②列表的时候，自变量的数值从小到大排列.

    ③x与y有无数多组，两边用省略号表示，如表2.

    课堂回放 师：在直角坐标系中描绘出这些点，它们在位置上有什么关系？（提示学生动用直尺去比对）

    生（齐）：在一条直线上.

    师：你还能找到哪些点？

    生4：（0.5，2），（1.5，4），（2.5，6）.

    生5：自变量也可以是负数，如（-0.5，0），（-1.5，-2），（-2.5，-4）.

    师：请大家描绘出刚刚两位同学所找的点，再观察这些点的位置.

    生6：这些点仍然在同一条直线上.

    师：刚才大家通过观察（图3），发现这些点位置上的特殊关系，能否保证函数图像所有的点都具有这样的特征？

    （学生小声议论，有一些迟疑）

    师：如果把自变量x在0到1之间10等分，横坐标分别取0.1，0.2，…，0.9，描绘出这些点（如图4），观察这些点的特征.

    （学生通过几何直观，發现这些点“靠”在一起形成了一条直线）

    师：扩大横轴上的单位长度，如图5，再观察这些点的位置.

    生（齐）：这些点又分开了.

    师：能使图像中的点“靠”得更近点吗？

    生7：0～1之间可以取更多的点，让点密集起来.

    师：能否具体点？

    生8：可以把自变量0～0.1，0.1～0.2，…，0.9～1再分别10等分.

    师：好，看图6.

    （学生的观察是点又形成了线）

    （2）初步小结：深化理解

    课堂回放 师：自变量在0～1之间还可以无数次等分下去，形成无数个点，它们会“靠”在一起形成一条线. 那么，1～2，2～3…同样如此.

    共同归纳：—次函数y=2x+1的图像是一条直线（如图7）.

    师：在这条直线上任意取点，如（-2，-3），（1，3），横坐标与纵坐标满足什么关系？

    生9：横坐标与纵坐标的数值满足一次函数的表达式.

    师：满足一次函数表达式的x和y转化为坐标是否也在函数图像上呢？

    师生总结：函数的图像与表达式之间是一一对应关系（如图8）.

    3. 深入探究：优化一次函数图像的画法

    学生活动2 已知一次函数y=-3x+2.

    （1）试判断（4，-10），（-3，8），（0，2）三点是否在函数y=-3x+2的图像上;

    （2）若（3，a），（b，7）两点在函数图像上，求a，b的值;

    （学生根据函数的表达式与图像之间的关系，迅速作答）

    （3）画出一次函数y=-3x+2的图像（限定时间1分钟）

    （1分钟后，有部分同学举手示意）

    课堂回放 师：你描了哪些点？

    生10：（0，2）和（1，-1）两个点.

    师：说说你的想法.

    生10：两点确定一条直线.

    师：能否舉例验证满足函数表达式的点都在如图9所示的直线上？

    师生互动：（借助几何画板）逐个描出学生列举出的点的坐标，如（-1，5），（-0.5，3.5），（0.5，0.5），（1.5，-2.5），（2，-4），如图10，得出满足函数表达式的点都在同一条直线上.

    师生共同总结：满足一次函数表达式的两个点就可以确定它的图像（“两点法”）.

    学生活动3 快速画出一次函数y=x+1的图像.

    课堂回放 师：哪些位置上的点的坐标比较容易确定？为什么？

    生11：两个坐标轴上的点的坐标容易确定，因为x轴上的点的纵坐标为0，y轴上的点的横坐标为0（板书如表3）.

    [x 0 -3 y 1 0 ][表3]

    师：根据这两个点的坐标，画出函数y=x+1的图像.

    师：对于一次函数的一般形式y=kx+b（k≠0），如何快速地找出两个点的坐标从而画出函数图像？

    生12：板书如表4.

    [x 0 - y b 0 ][表4]

    4. 回顾思考：知识的梳理及小结

    （1）对于函数h=（t-2）2+1（0≤t≤5）的图像，能否找到方法验证猜想？

    （2）一次函数的图像是直线，对此你有哪些认知？

    （3）一次函数的表达式与它的图像有何关系？

    （4）怎样画一次函数的图像？

    课堂回放 学生回答，教师补充点评.

    教学思考

    1. 深入探究，注重数学理解

    张奠宙先生把数学教学认为是数学教育形态的教学[1]. 数学教育形态的本质是教师创造数学理解. 数学理解是建立在循序渐进的认知过程基础上的，根据数学的思想与方法、知识与技能，探究数学知识的发生与发展过程. 对于教材中的概念、定理、法则，进行课堂教学时，需要教师对教学内容进行符合实际教学情况的改造与演绎. 所以，教师在教学中的真正价值体现，在于对数学理解的把握.

    笔者就这节课的理解，体现在两个层面：一是如何引导学生画函数图像. 本课的情境引入是抛物线的研究，渗透画函数图像的三个步骤. 对于一次函数图像的画法，则采用类比探究的方式. 过程中，表格中自变量x如何选取、点的坐标如何确定、由描绘的一个个孤立的点如何确定函数的图像，是本节课创造数学理解的关键. 二是如何验证一次函数的图像是一条直线. 随着课堂探究的深入，学生经历了感受（列表、描点），形成了感知（判断一次函数的图像是一条直线）. 当然，学生如何形成感悟，成为本节课数学理解的核心. 探究过程中，笔者引导学生仍从“点”出发，强化函数的图像是由无数个点形成的，采用了从“局部”到“整体”的思维方式. 例如图5中，自变量0～1之间取10等分，观察这些点的位置. 通过控制直角坐标系的单位长度，可以进一步把自变量在0～0.1，0.1～0.2，…，0.9～1之间再各自10等分，让更多满足函数表达式的点“密布”. 这样的方式能让学生通过图形感知理解——这些无数个“密布”的点“靠”在一起，就“连”成了一条直线.

    2. 鼓励质疑，促进课堂动态生成

    “学贵有疑，疑而出新. ”实际教学中，教师对于学生的质疑要适时鼓励，要给予他们创造性思考的信心. 例如，本节课“问题情境”中的二次函数图像，描点后连线（如图2），部分同学提出质疑：图像为何是曲线而不是折线？学生在没有任何认知的前提下，大胆地提出了他们的想法. 此时除给予鼓励外，还要抓住学生课堂中生成的问题，设置悬念，激发学生的探究兴趣[2]，同时为确定一次函数的图像做铺垫. 探究得出一次函数的图像是一条直线后，再次回到“问题情境”，确定二次函数图像的问题，根据一次函数探究的认知理论，学生较易找出验证的方法，这完全立足于学生的最近发展区.

    3. 立足于教学体系，遵循逻辑关系

    学习完一次函数的概念及表达式后，学生对函数的理解还较为抽象，那如何让函数更为具体地表示，强化学生对函数的认知与理解呢？函数图像的引入，是通过图形来刻画抽象的表达式，做到了“数”与“形”的对应. 在教学环节设计的过程中，教学内容的落脚点首先是感受画函数图像的方法步骤，然后通过描出点的位置猜想函数图像，自然螺旋上升到函数图像的验证. 探究过程中对于函数图像的感受、猜想、验证，最终都是让学生能够理解性地熟练刻画一次函数的图像. 基于研究性的数学教学，以灵动高效的课堂作为支撑，既能满足学生“知其然”，更追求“知其所以然”.

    参考文献：

    [1]张奠宙. 教育数学是具有教育形态的数学[J]. 数学教育学报，2005，14（3）：1-4.

    [2]黄文光，郦兴江. 理解“三个理解”? ? 凸显数学思想[J]. 中学数学，2015（2）：55-56.