“再建构”在初中数学试卷讲评课有效运用的研究
[摘? 要] 在初中数学教学中,试卷讲评课是一种重要的课型. “再建构”思想是从李庾南老师“自学·议论·引导”教学法提炼出来的,将再建构的思想与错题集的运用结合起来,能让学生更好地在大脑中对错题进行精加工和再建构.
[关键词] 初中数学;试卷讲评;再建构
在初中数学教学中,试卷讲评课是一种重要的课型,学生在一个阶段的数学学习过程中所形成的知识结构与能力,要接受以考试为主要形式的评价. 而讲评课的开展情况,直接决定了学生能否科学地面对考试中出现的各种结果,进而有效地促进学生对所学的知識进行再次理解与巩固. 传统的试卷讲评,通常都是以教师为主导的,越是认真负责的老师,越是会分析学生在考试中所犯的错误,很多时候老师还会整理不同学生所犯错误的类型,然后进行归类,以提高试卷讲评课的效果. 应当说这样的努力是有成效的,但同时我们也应当看到,在这样的讲评模式中,学生基本上还是处于被动接受的状态,也就是说学生没有一个主动发现并认识自己在考试中的错误的空间,从能力培养的角度来看,这样的讲评课模式亟待改革. 基于这样的思考,笔者借助“再建构”的思想并将其运用于初中数学试卷讲评课中,取得了一些收获.
“再建构”对初中数学试卷讲评课的启发
“再建构”思想是从“学材再建构”中提取出来的,“学材再建构”源于李庾南老师“自学·议论·引导”教学法中“重组教材内容,实施单元教学”的思想,必须遵循“以课程标准为基准,以教科书为参照,以教学对象(学生)为依据”的原则,并以“学生最大发展”为旨归,根据学习任务,为实现学习效益的最大化,对各种学材进行主动加工重构,其主要表现形式为“单元教学法”.
虽然说试卷讲评不同于单元教学,但是将“学材再建构”的思想,提炼为“再建构”思想,对初中数学试卷讲评课仍然有着很大的启发,这是因为初中数学试卷讲评课也有着为“学生最大发展”而努力的教学目标. 相对于新的知识教学而言,试卷讲评往往是通过对学生的引导,让学生对已经学过的数学知识尤其是对数学知识的应用有一个深刻的了解. 当将“学”转化为“用”的时候,其实就是学生能力提升的时候,这个时候学生需要对数学知识如何运用产生直觉性的认识,这样才能保证他们在考试的时候,能够第一时间准确找到解题的方向与工具(即具体的数学知识). 这个时候如果让学生本着再建构的思想,那他们就能跳出在新知学习中形成的对数学知识的线性认识,进而对这些知识进行重新建构,以加深对这些知识的了解,并且将数学知识转化为数学解题的能力.
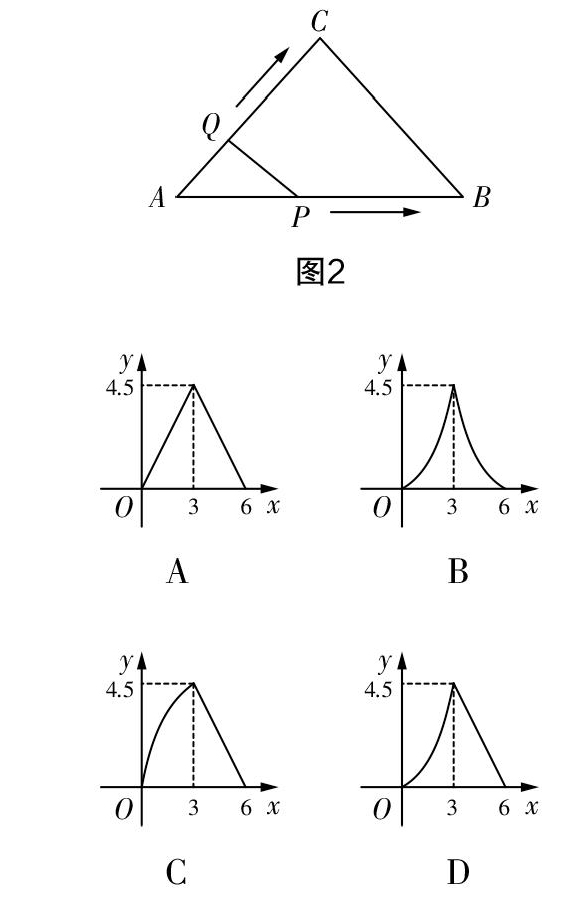
例如在函数图像题中,有时候我们需要学生对题目提供的信息进行转换,而这种转换能力在再建构的过程中就能够很好地形成. 在一次考试中,试卷上有这样的一道题目:
如图1,一段抛物线y=-x2+4(-2≤x≤2)为C1,与x轴交于A0,A1两点,顶点为D1;将C1绕点A1旋转180°得到C2,顶点为D2;C1与C2组成一个新的图像,垂直于y轴的直线l与新图像交于点P1(x1,y1),P2(x2,y2),与线段D1D2交于点P3(x3,y3),设x1,x2,x3均为正数,t=x1+x2+x3,则t的取值范围是(? ? )
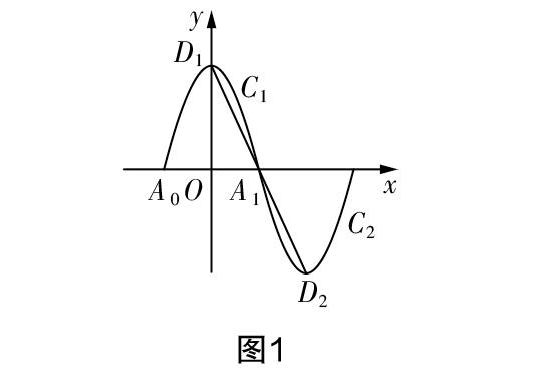
A. 6 C. 10 很多学生在考试中做这道题目的时候,都不知道如何进行转换. 在试卷讲评课中,笔者引导学生先自主思考,然后再进行合作学习,这两步都围绕一个中心问题,就是“题目中的抛物线发生了旋转之后,我们应当通过什么来描述它的变化?”这个中心问题直接引导学生生成了寻找旋转后的抛物线的解析式的认识,而一旦有了这个认识,他们就能迅速证明x1+x2=8,由2≤x3≤4,推出10≤x1+x2+x3≤12,然后结合旋转后的抛物线的解析式为y=(x-4)2-4=x2-8x+12,从而完成对问题的求解. 通过这样的再建构思想的运用,学生其实就形成了对此类函数图像题的解题思路,这是学生通过自我探究形成的解题思路,对应着学生的解题能力,也就是说这是一个能力培养的过程. 这也再次提醒我们以教师的“教”为中心,学生面对自己的错题再重新做一遍的试卷讲评方式,很难实现“优化学生知识结构、提炼数学思想方法、提升学生解题能力”的价值,而再建构却是化解这一矛盾的最佳方法. “再建构”在初中数学试卷讲评课中的应用 在利用“再建构”思想提高初中数学试卷讲评课效益的过程中,我们高度重视应用的有效性. 同时在研究的过程中,我们也积极借鉴其他人的研究成果,有同行对部分地区的高考状元进行过研究,研究结果发现这些高考状元之所以能够在高考中取得好成绩,除了长期积累和不懈努力外,更重要的是高度重视学习中所犯的错误. 他们有好几本错题集,只要是犯过的错误都认真记录下来,认真反思研究,决不一错再错. 错题集在初中数学教学中也是常用的一种教学策略,但是很多时候我们发现错题集并不能发挥预期中的作用,于是很多人弃若敝屣. 而笔者在通过比较研究后发现,我们更加需要的可能不是错题集这种形式,而应当是将再建构的思想与错题集的运用结合起来,以让学生在面对自己所做的错题时,能够更好地在大脑中对所做的错题进行精加工和再建构. 例如,同样是函数图像题,试卷上出现了一道错误率较高的题目: 如图2,在△ABC中,∠C=90°,AC=BC=3 cm,动点P从点A出发,以 cm/s的速度沿AB方向运动到点B,动点Q同时从点A出发,以1 cm/s的速度沿折线AC→CB方向运动到点B. 设△APQ的面积为y(cm2),运动时间为x(s),则下列图像能反映y与x之间关系的是(? ? ) 在试卷讲评课上,面对这道题目的时候,笔者先组织学生进行讨论交流,每组安排了一个将本题做对的同学作为组长,然后让组长将自己的解题思路讲给同组的同学听. 考虑到本题有一定的难度,所以在这一步设计当中笔者并没有期待组长的讲解能够解决所有问题,目的只是通过组长的讲解,让学生先对解题思路形成一个印象. 等到这个印象初步形成之后,笔者引导学生将自己在理解组长思路的过程中出现的困惑一一表达出来. 实践表明,正是设计了这样的一个表达环节,大多数学生才有机会对解题思路进行重新理解与建构,因而使解题思路更加清晰. 在五人学习小组中,除了组长之外,通常都有两至三个学生能够自主总结出解题思路,比如说就有学生能够很清晰地总结:作QD⊥AB,分点Q在AC,CB上运动这两种情况,然后根据直角三角形的性质表示出QD的长,再利用三角形面积公式得出函数解析式即可判断. 这样的表述可谓是非常准确. 很大程度上讲,能够有这样的教学效果,完全取决于再建构思想在试卷讲评课上的运用. “再建构”应用于初中数学试卷讲评课的思考 基于对李庾南老师“自学·议论·引导”教学法的学习,我们已经知道了“再建构”教学实际上就是指根据数学知识发生的规律及其内在联系、学生学习的基础与可达到的高度以及思维发展水平,将学材(知识)分为不同的单元或模块,分课时实施,便于学生从整体上理解和掌握,进而习得学习方法,优化思维品质. 将这一思想运用于初中数学试卷讲评课,给我们带来的思考非常多,而且是非常有益的. 我们发现试卷讲评课的效益提升,关键取决于学生在试卷讲评的过程中,思维如何打开,又怎样才能具有一个较大的思维空间. 而这些问题的回答,都可以在“再建构”的思想中寻找到答案,这在客观上说明再建构思想确实有着非常强的生命力. 当然,对于一线教师而言,“再建构”教学可能还有更多的思想未被发掘出来,需要我们在包括试卷讲评课的教学研究中进一步探讨.作者简介:冒劼(1981-),本科学历,中学一级教师,如皋市学科带头人,从事初中数学教学工作.

