“多变”的角平分线

    王金金

    

    

    

    [摘? 要] 教学中，我们必须让学生在解题与应用的过程中知其然，而且知其所以然，并通过总结、分析、对比和反思达成对方法与思想的理解与应用，促进学生真正理解. 文章结合“多变”的角平分线来诠释这一策略达成.

    [关键词] 几何;角平分线;初中数学

    角平分线是初中几何图形中的常见线段，在几何证明题中运用较为广泛. 角平分线的定理和逆定理是学生们所熟知的，通常将此作为解决几何问题的辅助手段. 除此之外，当角平分线与等线段、垂线、平行线、圆结合在一起时，往往可以得到一些新的结论，而这些结论正是解决几何问题的钥匙. 下文笔者就盘点几类与角平分线有关的几何问题模型，供大家参考.

    截等长，现全等

    “等角”是角平分线在几何问题中最直观的结论，并且这两个角是有着一条公共边的角，这时，只要两个角对应的另外一条边相等，由“SAS”即可出现全等三角形.

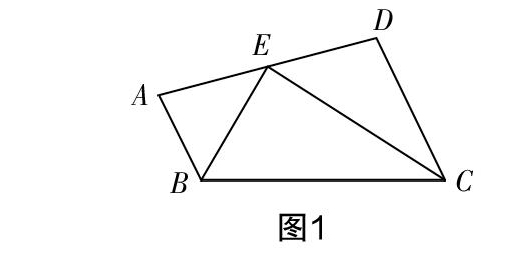
    例1如图1，AB∥CD，BE平分∠ABC，点E在AD上，求证：BC=AB+CD.

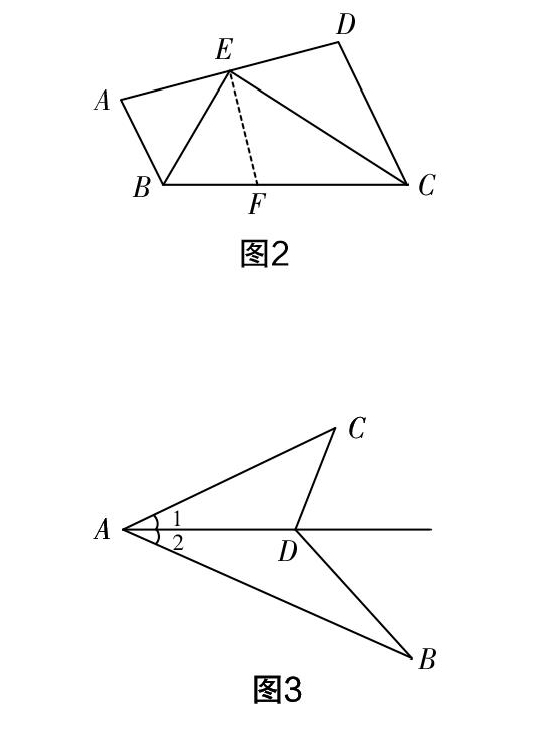
    分析? 求证线段的和差关系通常用“割长补短”法，即将最长的线段分割成两段或将其中一条较短线段延长到和最长的线段一样. 在此题中可在较长线段BC上截取BF=AB，如图2，由角平分线得到∠ABE=EBF，再由BE=BE，AB=FB证得△AEB与△FEB全等，由此得到∠AEB=∠FEB，推出∠FEC=∠DEC，证出△FEC与△DEC全等，得到FC=DC，从而证出结论. 上述方法是“割长”，也可以延长BE与CD的延长线交于一点来证明.

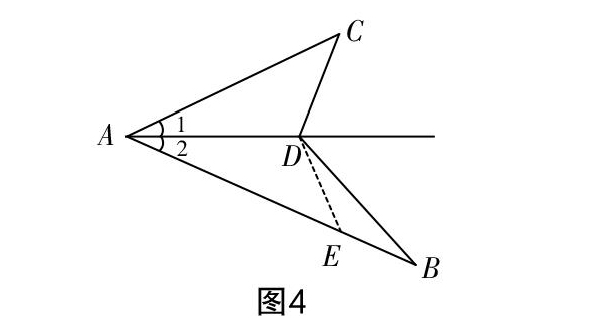
    例2如图3，AB>AC，∠1=∠2，求证：AB-AC>BD-CD.

    分析? 线段和差的不等关系的证明通常由三角形三边长的关系来实现. 在AB上取点E，使得AE=AC，通过证明△ADC与△ADE全等得到CD=DE，再结合△EBD三边的关系即可证.

    三角形问题中，构造全等是运用最为广泛的证明等量关系的方法. 角平分线将一个角分成两个相等的角是其最明显的性质，同时角平分线还是这两个角的公共边，这样就为全等创造了一组边和一组角，再寻找出另外一条边即可实现全等的证明.

    遇平行，成等腰

    由角平分线可以得到相等的角，由平行线也可以得出相等的角，两者结合，即可将等角转化至同一个三角形中，构造出等腰三角形，在相应的几何证明题中得到解题的关键性结论.

    例3如图5，已知四边形ABCD为平行四边形，∠BAD的平分线AE交CD于点F，交BC的延长线于点E，求证：BE=CD.

    分析? 由四边形ABCD为平行四边形可将BE=CD转化成证明BE=AB，即证明△ABE为等腰三角形. 因此联想到“等角对等边”，将边的问题转化为角的问题. 对由角平分线得到的∠BAE=∠DAE与由平行关系得到的∠DAE=∠AEB进行等量代换即可证出.

    例4如图6，OP平分∠AOB，∠AOP=15°，PC∥OA，PD⊥OA于点D，PC=4，求PD的长.

    分析? 通过找出与所求线段相等的线段是求线段长度较为常见的方法. 此题可以首先由OP平分∠AOB，结合PC∥OA得出△OCP为等腰三角形，接着截取OE=OC可证△OEP与△OCP全等，如图7，得出PE=PC=4，再由外角与内角的关系得到∠PED=30°，因此PD=PE=2.

    平行线和角平分线结合在一起出现的等腰三角形通常是几何问题中的隐含条件，如将此隐含条件挖掘出来，对该类几何问题的解决有很大帮助. 另外，若题目中要求的线段在一个非特殊角的直角三角形中，通常要用转化、平移或旋转的方法将所求的线段转移至含有特殊角的直角三角形中来解决.

    三线合，变等腰

    “等角对等边”是证明等腰三角形最常用的方法，除此之外，“三线合一”也是判定三角形为等腰三角形的方法之一. 角平分线可以给三角形提供三线之一，如果角平分线再遇上中线或高线，则等腰三角形就出现了.

    例5如图8，AB=AC，∠BAC=90°，BD为∠ABC的平分线，CE⊥BE，求证：BD=2CE.

    分析? 由角平分线与CE⊥BE得到的高线已经给等腰三角形创造了两个条件，因此只需将BA与CE延长至相交，即可通过全等证出△BCF是等腰三角形，因此E是CF的中点，CF=2CE，随后证明△FAC与△DAB全等即可.

    例6如图10所示，D是△ABC内的一点，∠CAD=∠BAD=10°，∠ABD=20°，∠CBD=40°，求∠BCD的度数.

    分析? 该问题将∠BCD的度数放至△BCD中. 首先延长AC到E，使AE=AB，再连接BE，DE，延长AD交BE于F，如图11. 由AF是等腰△ABE的顶角平分线可知AF垂直平分BE. 从而DB=DE，再由∠BDF=∠DAB+∠DBA=30°可知∠BDE=60°，因此△BDE是等边三角形. 可以算出∠BCE=∠BEC=80°，得到BC=BE=BD，则∠BCD=（180°-40°）÷2=70°.

    上述两题的突破口都是将角平分作为等腰三角形的顶角平分线来解决问题. 尤其是例6，首先利用角平分线构造等腰三角形，再利用“三线合一”得出等腰三角形，后通过已知度数求出60°角得到等边三角形，再由度数得到等腰三角形求解. 过程有点繁杂，但构造等腰三角形是解题的方向与关键.

    置圆内，等弧弦

    圆是初中几何的重要内容，将圆与三角形相结合也是初中数学常见的几何问题. 将角平分线所得到的等角置于圆内，就成了圆周角或圆心角，通常能得到等弧和等弦，为问题的进一步解决提供条件.

    例7如图12，△ABC内接于☉O，∠ACB=90°，∠ACB的平分线交☉O于点D，若AC=6，BD=5，求BC的长.

    分析? 求BC的长，只需将BC看成是直角三角形△ACB的一条边，利用勾股定理即可. 由题已知AC=6，还需求AB的长度. 此时连接AD，如图13，由角平分线可知圆周角∠ACD=∠BCD，所以AD=BD，△ADB是等腰直角三角形，由BD=5可算出AB的長，进而求出BC.

    例8如图14，∠BAC的平分线交△ABC的外接圆与点D，∠ABC的平分线交AD于点E.

    （1）求证：DE=DB.

    （2）若∠BAC=90°，BD=4，求△ABC的外接圆半径.

    分析? 解决（1）只需用角的和差与三角形内角与外角的关系. 已知∠BED=∠BAE+∠ABE，∠EBD=∠EBC+∠CBD. 由BE平分∠ABC可知∠ABE=∠EBC，由AD平分∠BAC可知∠BAE=∠CAD，又∠CAD=∠CBD，所以∠BAE=∠CBD. 因此∠BED=∠EBD，DE=DB. 在（2）中，连接CD，如图15所示，由角平分线得∠BAD=∠CBD，所以BD=CD，△BDC是等腰直角三角形，即可根据BD的长度求出直径，进而再求半径.

    由角平分线对应的等角得到等弧和等弦均是以上两个例题的关键步骤. 等弧和等弦加上直径就会构成等腰直角三角形，可以将问题简化. 角平分线所对应的等角加上同弧所对应的等角通常可以实现等角之间的转化，为圆内等量关系的讨论增加一条道路.

    角平分线不仅仅是一条射线或线段，深层挖掘，它还可以承载更多，“多变”的角平分线，能让问题更多姿，让几何更精彩.

    总结规律是引导学生学会解决几何问题的基本思路和提高几何教学的重要手段. 在几何问题中，学生往往感觉困难的是无法对所给的条件深层加工，得到有用的结论，找不到考虑问题的正确方向. 教师在几何教学时，尤其是总复习阶段，广泛做题，将问题分类研究，总结各类问题的常见几何模型和思路方向，可以让学生觉得几何有规律可循，几何问题并无想象中困难，从而改变其对几何问题的态度，提高解决问题的能力.