2014年鲁甸6.5级地震强震动频率非平稳特性相关分析
刘琼仙 邱志刚 杨黎薇 林国良


摘要:以2014年云南鲁甸6.5级地震的加速度记录为研究样本,分别对强震动三分量的加速度时程进行持续时间与穿零率分析,通过对三分量记录间频率特性差异的研究,总结了鲁甸6.5级地震中强震动记录三个分量的相对峰值持时离散特点,以及穿零率随震中距的走势特征,侧重分析了强震动频率的非平稳变化。
关键词:鲁甸地震;频率非平稳特性;持时;穿零特性
中图分类号:P315.9 文献标识码:A 文章编号:1000-0666(2016)04-0613-09
0 引言
地震动过程的频率非平稳特性研究近几年来引起了较多的关注和重视(廖振鹏,1994),研究地震动频率非平稳的特性,是作为分析结构弹塑性反应的一个重要因素。地震动时程的强度和频率非平稳特性对于结构物对非线性地震动力的反应具有不可忽略的影响,国内多位学者主要是从理论上对地震动非平稳特性机制进行了分析和讨论,同时以国内外获取的强震动记录为基础数据对该特性进行了进一步的研究。赵凤新和胡聿贤(1994)在讨论地震动强度、频率非平稳性与幅值谱和相位差谱关系的基础上,对地震动非平稳性作用的机制作了进一步的分析。王君杰和周晶(1997)应用合成的人工地震加速度时程作为输入,计算了一个框架结构建筑的地震反应,得出了人工合成的用于结构抗震设计的地震加速度时程时呈现出的地震动频谱非平稳特性。李英民等(2000)通过穿零率研究地震动频率的非平稳特性,进行了三维地震动穿零率参数相关性的统计分析,给出三维相关的参数取值建议。王国权等(2001,2003)以“9·21”台湾集集地震的30组近断层加速度时程为样本,研究了周期频率和幅值的随机特性,并对30级数据的相关特性进行分析,结果表明,三分量(东西、南北、垂直)集系上的自相关、互相关矩阵的三分量加速度时程均为非平稳随机过程,且相关系数的分布也是随机的,无法用确定的数字模型来模拟。董娣等(2006)采用美国、日本、墨西哥、台湾集集地震和其它地区在基岩场地上的156组共468条强震动记录作为基础数据,按地震的震级、震中距分组分析了持续时间随震级、震中距的变化规律,并利用这些记录对其穿零特性进行了研究,结果表明,穿零率随着时间的变化呈现出了频率的非平稳性,在一定程度上反映了地震动的时频变化特性。“九五”“十五”期间,我国强震动台网建设得到了快速发展(卢大伟,李小军,2010),在2007年后的多次强震中获取了一定数量的近断层强震动记录。2008年5月12日的汶川8.0级地震,中国强震动台网获取了数千条强震动记录,谢俊举等(2011)利用这些记录,对近断层地震动的强度和频率的非平稳特征进行研究,并对其非平稳特征原因进行初步分析,结果表明在近断层的地震动出现了明显的非平稳性。杨黎薇等(2016)利用2014年10月7日景谷6.6级地震的37组加速度记录为分析样本,研究总结了景谷地震强震动的非平稳特性。
地震动频域非平稳特性描述目前主要方法有两大类:一类是利用能够反映地震动频域非平稳特性的某些特征量作描述,如穿零率特征,这类方法主要考虑能反映地震动时频非平稳特性某些特征量的变化规律,在客观描述地震动非平稳特性上具有较好效果;另一类是利用现代时频分析手段对地震动频域非平稳特性进行定量描述,如傅里叶变换法,该方法的分析能够反应出地震动能量在频率上的分布,却不能反映地震动频率与时间相关的非平稳特性。本文选取2014年8月3日云南鲁甸6.5级地震的58组共174条(每组3条记录,包括竖直向 UD,北南向 NS 和东西向EW)加速度记录为研究样本,利用穿零率特征法分别对强震动三分量的加速度时程进行持续时间与穿零率进行分析,对三分量场地时变特性进行讨论,初步总结鲁甸6.5级地震的强震动频率非平稳特性,并对主震记录强震动数据进行相关分析。
1 统计数据基础
中国数字强震动台网布设于云南、四川省周边的共80个强震动台站获取了这次地震的主震记录,本文挑选其中有代表性的记录共58组强震数据进行计算分析,所选地震动记录采样频率均为200 sps,图1为地震震中与选取的58个强震动台站分布情况。
2 持时特性分析
持续时间(简称持时)主要作为描述地震动强度变化的指标去体现其对地震动破坏性作用的影响力。记录持时包括绝对持时和相对持时,绝对持时主要是Bolt括号持时,它以记录的加速度绝对峰值首次和末次达到或超过规定值(0.1 g,0.05 g)所经历的时间段作为持时定义(谢礼立,周雍年,1984),一般较少采用,尤其是远震记录较多时,会出现零值持时。相对持时包括Kawashinat括号持时、二阶矩持时和Husid持时,本文采用其中的Kawashinat括号持时定义,以首末两次到达或者超过加速度最大峰值的几分之一之间的时段长度为持时,由于它是根据加速度峰值的分数值来确定,也称为分数持时或相对峰值持时,可选用的分数通常在1/5~1/2之间,本文选用0.3来进行计算分析(赵艳等,2007)。
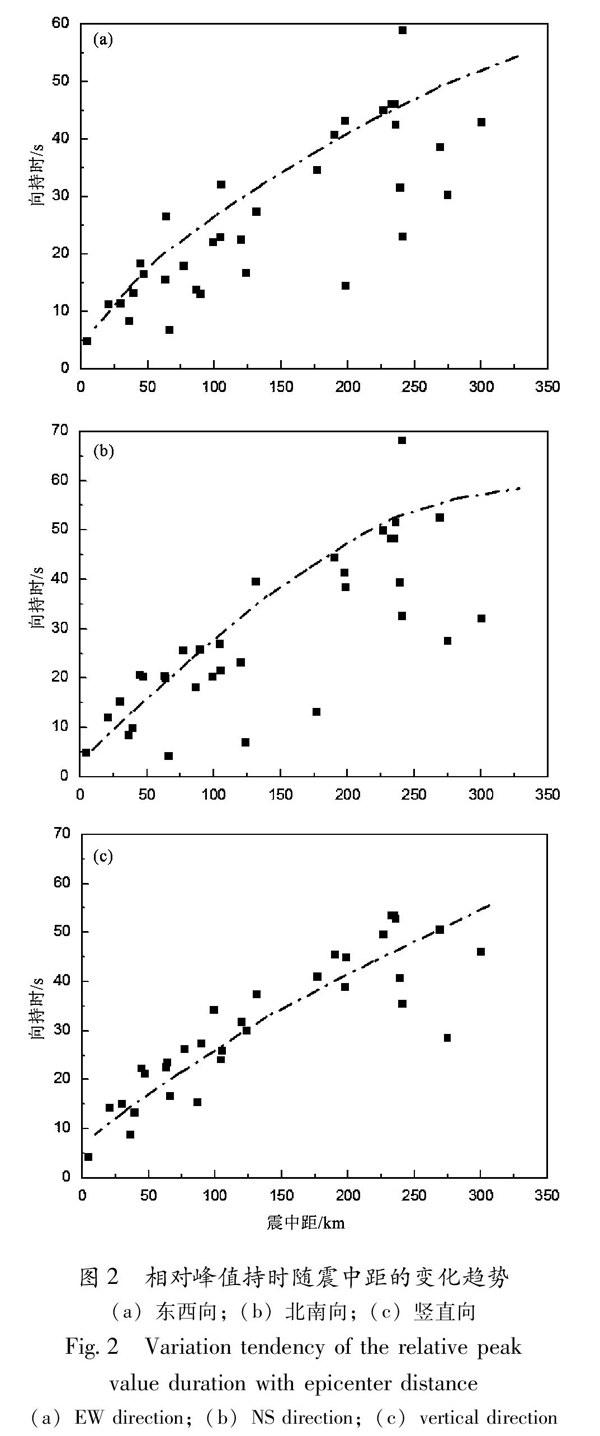
以2014年8月3日鲁甸6.5级地震获取所有强震动记录为数据基础,经校正处理后,挑选出川滇地区的可用记录进行持时计算。挑选出的强震动记录中,距离震中最近的龙头山台震中距为4.38 km,最远的九河乡台站震中距为333.97 km,几十个记录分布于不同震中距内,部分计算结果如表1所示,三分量持时随震中距的变化如图2所示。
由于地震动强度很低时阈值触发会导致强震动加速度记录不完整,故而在统计过程中需将PGA小于0.3倍设定触发阈值的记录剔除。
由图2a可见,东西分量的相对峰值持时最小持时为5 s,其震中距是4.38 km,最大持时为66.885 s,其震中距是245.94 km,持时随着震中距增大而增大。
由图2b可见,北南分量的相对峰值持时最小持时为4.94 s,其震中距是4.38 km,最大持时为82.925 s,其震中距是234.84 km。随着震中距的变化趋势其持时比东西分量更为明显,持时随着震中距增大而增大的幅度高于东西分量。
由图2c可见,竖直分量的相对峰值最小持时为4.28 s,其震中距是4.38 km,最大持时为89.62 s,其震中距是234.84 km。其持时随着震中距的变化最为清晰,明显是随着震中距增大而增大。
综上所述,鲁甸6.5级地震所计算得到的强震动记录持时,三分量的相对峰值持时中水平分量的离散性大于竖直分量的离散性,持时随着震中距的变化,整体上是离散分布于0~45 s范围内,且持时随着震中距增大而增大。
将三分量的相对峰值持时随震中距变化趋势拟合为直线表达,如图3所示。由图3可见,竖直分量增大与减小走势最强,其次是北南分量,最后是东西分量。
3 穿零率相关特性
本文用单位时间内地震波穿过零点的次数(即穿零率)来反映地震波的周期随时间变化特征,零点为地震波曲线与横轴(零线)的相交点。穿零率随时间的变化可体现频率的非平稳性,在一定程度上反映了地震动的时频变化特性,同时,穿零率也在一定程度上描述出地震波的周期特征,通常情况下,穿零率越大,相应的周期就会越小,频率就越高(杨黎薇等,2016)。
3.1 实例分析
归一化是一种无量纲处理手段,主要是使物理系数值的绝对值变成某种相对值的关系,这种方法是简化计算、缩小量值最有效的方法。本文拟采用线性函数法中的最大最小值法进行归一化处理,即将样本数据归一化到范围内,采用方法的公式为
y(k)=〔x(k)-min(x(n))〕/〔max(x(n))-min(x(n))〕.(1)
其中,x(n)表示样本数据,n=1,2,……N;k=1,2,……N;min(x(n))表示样本数据x(n)的最小值;max(x(n))表示样本数据x(n)的最大值。
为了消除地震波记录触发时刻与末端时刻的边界影响,本文取每条记录 P 波初动前5 s至整个地震波形结束后5 s这一时间段为研究对象,同时,将穿零率曲线横轴的时间与纵轴的穿零率一致经过归一化处理,即时间在0~1之间变化,穿零率在0~1之间变化,以满足不同条件下的穿零率具有的可对比性。为保证统计结果的一致性,本节以上节选取的记录为基础,全面了解震中距对强震动记录穿零率的影响。将强震动记录按震中距为0~20 km、20~60 km、60~100 km、100~200 km以及200 km以上这5种情况分组,分别算出各分向对应穿零率的均值。
图4 a~e代表了5种不同震中距分组条件下,东西分量记录的穿零率曲线异同。整体来看,穿零率曲线均为不规则震荡的随机曲线,可见地震波有较为复杂的周期成分,且随着时间增长,穿零率整体上有逐渐减小的趋势。通过对不同震中距的对比发现,震中距在60 km范围内的穿零次数明显小于震中距大于60 km的穿零次数,且随着震中距增加,地震动的低频成分更加丰富。图4f以线性方式绘出了不同震中距条件下东西分量穿零率均值的走势。由图4f可见,震中距20~60 km范围内的穿零率随着时间增长衰减下降最快,其次是震中距60~100 km范围内的穿零率衰减,再者是震中距100~200 km范围内的穿零率衰减,衰减最慢的穿零率震中距已超过200 km。
图5a~e代表了5种不同震中距分组条件下,北南分量记录的穿零率曲线异同。整体来看,其穿零率曲线所有变化与东西分量相似,在此不做过多介绍。相比东西分量的穿零次数,当震中距大于60 km后,北南分量的穿零次数就明显增加。图5f以线性方式绘出了不同震中距条件下北南分量穿零率均值的走势,该分量穿零率的衰减速度随着震中距增大而减小。
图6a~e代表了5种不同震中距分组条件下,竖直分量记录的穿零率曲线异同。与水平分量相比,竖直分量记录穿零曲线的穿零次数明显增多。图6f线性方式绘出了不同震中距条件下竖直分量穿零率均值的走势,该分量穿零率的衰减速度随着震中距增大而减小。
综上而论,穿零率曲线的不规则随机震荡特性表现了地震波复杂的周期成分。随着时间增长,三分量的穿零率呈减小趋势;随着震中距增加,三分量的穿零次数明显增多,即地震波的振动幅度随着震中距增大呈减小趋势,且振动频率随震中距增大而增快。同时可见,震中距越大,穿零率随着时间的衰减越慢。
3.2 穿零率拟合曲线变化
由上节分析与图示可知,地震波穿零率成分复杂,以最简洁的线性拟合来描述穿零曲线特性,可清晰直观了解穿零曲线的相关特性。
图7a~d代表了三分量的穿零率在不同震中距条件下随着时间增长的衰减变化。总体而言,竖直分量记录的穿零率大于水平分量的穿零率,可见竖直分量加速度记录中高频成分更多一些,此外,竖直分量的穿零率随时间的衰减最慢,水平分量的穿零率衰减速度相差不大。
4 结论
本文以2014年8月3日云南鲁甸6.5级地震中的58组强震动记录为基础,详尽分析了相对峰值持时随震中距的变化规律,并按不同震中距分布统计研究穿零率的特性,以此了解本次强震动频率的非平稳性。研究表明,云南鲁甸6.5级地震动频率非平稳性有以下特征:
(1)三分量的相对峰值持时水平分量的离散性大于竖直分量的离散性,持时随着震中距的变化,整体上是离散分布于0秒至45秒范围内,且持时随着震中距增大而增大。
(2)随着时间增长,三分量的穿零率呈减小趋势;随着震中距增大,三分量的穿零次数也明显增长,即地震波的振动幅度随着震中距增大呈减小趋势,振动频率随着震中距增大而速度增快。同时可见,震中距越大,地震动所包含的低频成分越多,且随着震中距增大,穿零率随着时间的衰减逐渐减慢。
(3)竖直分量记录的穿零率大于水平分量,且竖直分量的穿零率随时间的衰减最慢,水平分量的穿零率衰减速度相差不大。
参考文献:
董娣,周锡元,徐国栋等.2006.强震记录频率非平稳特性的若干研究.地震工程与工程振动,26(1):22-29.
李英民,赖明,白绍良.2000.三维地震动频率非平稳特性的相关性研究.重庆建筑大学学报,22(增刊1):22-26.
廖振鹏.1994.强烈地震地面运行模拟.北京:地震出版社.
卢大伟,李小军.2010.中国大陆强震动观测发展研究.国际地震动态,(10):35-42.
王国权,周锡元,马宗晋等.2001.921台湾地震近断层强地面运动的周期和幅值特性.工程抗震,(1):30-36.
王国权,周锡元.2003.台湾集集地震近断层强震地面运动加速度时程的随机特性.防灾减灾工程学报,23(4):10-19.
王君杰,周晶.1997.地震动频谱平稳性对结构非线性反应的影响.地震工程与工程振动,17(2):16-20.
谢俊举,温增平,高孟潭等.2011.2008年汶川地震近断层地震动的非平稳特征.地球物理学报,54(3):728-736.
谢礼立,周雍年.1984.一个新的地震动持续时间定义.地震工程与工程振动,4(2):27-35.
杨黎薇,邱志刚,崔建文等.2016.2014年景谷6.6级强地震动频率非平稳特性研究.北京:强震动观测与应用研讨会论文集,68-82.
赵凤新,胡聿贤.1994.地震动非平稳性与幅值谱和相位差谱的关系.地震工程与工程振动,14(2):1-6.
赵艳,郭明珠,季杨等.2007.场地条件对地震动持时的影响.震灾防御技术,2(4):417-424.



摘要:以2014年云南鲁甸6.5级地震的加速度记录为研究样本,分别对强震动三分量的加速度时程进行持续时间与穿零率分析,通过对三分量记录间频率特性差异的研究,总结了鲁甸6.5级地震中强震动记录三个分量的相对峰值持时离散特点,以及穿零率随震中距的走势特征,侧重分析了强震动频率的非平稳变化。
关键词:鲁甸地震;频率非平稳特性;持时;穿零特性
中图分类号:P315.9 文献标识码:A 文章编号:1000-0666(2016)04-0613-09
0 引言
地震动过程的频率非平稳特性研究近几年来引起了较多的关注和重视(廖振鹏,1994),研究地震动频率非平稳的特性,是作为分析结构弹塑性反应的一个重要因素。地震动时程的强度和频率非平稳特性对于结构物对非线性地震动力的反应具有不可忽略的影响,国内多位学者主要是从理论上对地震动非平稳特性机制进行了分析和讨论,同时以国内外获取的强震动记录为基础数据对该特性进行了进一步的研究。赵凤新和胡聿贤(1994)在讨论地震动强度、频率非平稳性与幅值谱和相位差谱关系的基础上,对地震动非平稳性作用的机制作了进一步的分析。王君杰和周晶(1997)应用合成的人工地震加速度时程作为输入,计算了一个框架结构建筑的地震反应,得出了人工合成的用于结构抗震设计的地震加速度时程时呈现出的地震动频谱非平稳特性。李英民等(2000)通过穿零率研究地震动频率的非平稳特性,进行了三维地震动穿零率参数相关性的统计分析,给出三维相关的参数取值建议。王国权等(2001,2003)以“9·21”台湾集集地震的30组近断层加速度时程为样本,研究了周期频率和幅值的随机特性,并对30级数据的相关特性进行分析,结果表明,三分量(东西、南北、垂直)集系上的自相关、互相关矩阵的三分量加速度时程均为非平稳随机过程,且相关系数的分布也是随机的,无法用确定的数字模型来模拟。董娣等(2006)采用美国、日本、墨西哥、台湾集集地震和其它地区在基岩场地上的156组共468条强震动记录作为基础数据,按地震的震级、震中距分组分析了持续时间随震级、震中距的变化规律,并利用这些记录对其穿零特性进行了研究,结果表明,穿零率随着时间的变化呈现出了频率的非平稳性,在一定程度上反映了地震动的时频变化特性。“九五”“十五”期间,我国强震动台网建设得到了快速发展(卢大伟,李小军,2010),在2007年后的多次强震中获取了一定数量的近断层强震动记录。2008年5月12日的汶川8.0级地震,中国强震动台网获取了数千条强震动记录,谢俊举等(2011)利用这些记录,对近断层地震动的强度和频率的非平稳特征进行研究,并对其非平稳特征原因进行初步分析,结果表明在近断层的地震动出现了明显的非平稳性。杨黎薇等(2016)利用2014年10月7日景谷6.6级地震的37组加速度记录为分析样本,研究总结了景谷地震强震动的非平稳特性。
地震动频域非平稳特性描述目前主要方法有两大类:一类是利用能够反映地震动频域非平稳特性的某些特征量作描述,如穿零率特征,这类方法主要考虑能反映地震动时频非平稳特性某些特征量的变化规律,在客观描述地震动非平稳特性上具有较好效果;另一类是利用现代时频分析手段对地震动频域非平稳特性进行定量描述,如傅里叶变换法,该方法的分析能够反应出地震动能量在频率上的分布,却不能反映地震动频率与时间相关的非平稳特性。本文选取2014年8月3日云南鲁甸6.5级地震的58组共174条(每组3条记录,包括竖直向 UD,北南向 NS 和东西向EW)加速度记录为研究样本,利用穿零率特征法分别对强震动三分量的加速度时程进行持续时间与穿零率进行分析,对三分量场地时变特性进行讨论,初步总结鲁甸6.5级地震的强震动频率非平稳特性,并对主震记录强震动数据进行相关分析。
1 统计数据基础
中国数字强震动台网布设于云南、四川省周边的共80个强震动台站获取了这次地震的主震记录,本文挑选其中有代表性的记录共58组强震数据进行计算分析,所选地震动记录采样频率均为200 sps,图1为地震震中与选取的58个强震动台站分布情况。
2 持时特性分析
持续时间(简称持时)主要作为描述地震动强度变化的指标去体现其对地震动破坏性作用的影响力。记录持时包括绝对持时和相对持时,绝对持时主要是Bolt括号持时,它以记录的加速度绝对峰值首次和末次达到或超过规定值(0.1 g,0.05 g)所经历的时间段作为持时定义(谢礼立,周雍年,1984),一般较少采用,尤其是远震记录较多时,会出现零值持时。相对持时包括Kawashinat括号持时、二阶矩持时和Husid持时,本文采用其中的Kawashinat括号持时定义,以首末两次到达或者超过加速度最大峰值的几分之一之间的时段长度为持时,由于它是根据加速度峰值的分数值来确定,也称为分数持时或相对峰值持时,可选用的分数通常在1/5~1/2之间,本文选用0.3来进行计算分析(赵艳等,2007)。
以2014年8月3日鲁甸6.5级地震获取所有强震动记录为数据基础,经校正处理后,挑选出川滇地区的可用记录进行持时计算。挑选出的强震动记录中,距离震中最近的龙头山台震中距为4.38 km,最远的九河乡台站震中距为333.97 km,几十个记录分布于不同震中距内,部分计算结果如表1所示,三分量持时随震中距的变化如图2所示。
由于地震动强度很低时阈值触发会导致强震动加速度记录不完整,故而在统计过程中需将PGA小于0.3倍设定触发阈值的记录剔除。
由图2a可见,东西分量的相对峰值持时最小持时为5 s,其震中距是4.38 km,最大持时为66.885 s,其震中距是245.94 km,持时随着震中距增大而增大。
由图2b可见,北南分量的相对峰值持时最小持时为4.94 s,其震中距是4.38 km,最大持时为82.925 s,其震中距是234.84 km。随着震中距的变化趋势其持时比东西分量更为明显,持时随着震中距增大而增大的幅度高于东西分量。
由图2c可见,竖直分量的相对峰值最小持时为4.28 s,其震中距是4.38 km,最大持时为89.62 s,其震中距是234.84 km。其持时随着震中距的变化最为清晰,明显是随着震中距增大而增大。
综上所述,鲁甸6.5级地震所计算得到的强震动记录持时,三分量的相对峰值持时中水平分量的离散性大于竖直分量的离散性,持时随着震中距的变化,整体上是离散分布于0~45 s范围内,且持时随着震中距增大而增大。
将三分量的相对峰值持时随震中距变化趋势拟合为直线表达,如图3所示。由图3可见,竖直分量增大与减小走势最强,其次是北南分量,最后是东西分量。
3 穿零率相关特性
本文用单位时间内地震波穿过零点的次数(即穿零率)来反映地震波的周期随时间变化特征,零点为地震波曲线与横轴(零线)的相交点。穿零率随时间的变化可体现频率的非平稳性,在一定程度上反映了地震动的时频变化特性,同时,穿零率也在一定程度上描述出地震波的周期特征,通常情况下,穿零率越大,相应的周期就会越小,频率就越高(杨黎薇等,2016)。
3.1 实例分析
归一化是一种无量纲处理手段,主要是使物理系数值的绝对值变成某种相对值的关系,这种方法是简化计算、缩小量值最有效的方法。本文拟采用线性函数法中的最大最小值法进行归一化处理,即将样本数据归一化到范围内,采用方法的公式为
y(k)=〔x(k)-min(x(n))〕/〔max(x(n))-min(x(n))〕.(1)
其中,x(n)表示样本数据,n=1,2,……N;k=1,2,……N;min(x(n))表示样本数据x(n)的最小值;max(x(n))表示样本数据x(n)的最大值。
为了消除地震波记录触发时刻与末端时刻的边界影响,本文取每条记录 P 波初动前5 s至整个地震波形结束后5 s这一时间段为研究对象,同时,将穿零率曲线横轴的时间与纵轴的穿零率一致经过归一化处理,即时间在0~1之间变化,穿零率在0~1之间变化,以满足不同条件下的穿零率具有的可对比性。为保证统计结果的一致性,本节以上节选取的记录为基础,全面了解震中距对强震动记录穿零率的影响。将强震动记录按震中距为0~20 km、20~60 km、60~100 km、100~200 km以及200 km以上这5种情况分组,分别算出各分向对应穿零率的均值。
图4 a~e代表了5种不同震中距分组条件下,东西分量记录的穿零率曲线异同。整体来看,穿零率曲线均为不规则震荡的随机曲线,可见地震波有较为复杂的周期成分,且随着时间增长,穿零率整体上有逐渐减小的趋势。通过对不同震中距的对比发现,震中距在60 km范围内的穿零次数明显小于震中距大于60 km的穿零次数,且随着震中距增加,地震动的低频成分更加丰富。图4f以线性方式绘出了不同震中距条件下东西分量穿零率均值的走势。由图4f可见,震中距20~60 km范围内的穿零率随着时间增长衰减下降最快,其次是震中距60~100 km范围内的穿零率衰减,再者是震中距100~200 km范围内的穿零率衰减,衰减最慢的穿零率震中距已超过200 km。
图5a~e代表了5种不同震中距分组条件下,北南分量记录的穿零率曲线异同。整体来看,其穿零率曲线所有变化与东西分量相似,在此不做过多介绍。相比东西分量的穿零次数,当震中距大于60 km后,北南分量的穿零次数就明显增加。图5f以线性方式绘出了不同震中距条件下北南分量穿零率均值的走势,该分量穿零率的衰减速度随着震中距增大而减小。
图6a~e代表了5种不同震中距分组条件下,竖直分量记录的穿零率曲线异同。与水平分量相比,竖直分量记录穿零曲线的穿零次数明显增多。图6f线性方式绘出了不同震中距条件下竖直分量穿零率均值的走势,该分量穿零率的衰减速度随着震中距增大而减小。
综上而论,穿零率曲线的不规则随机震荡特性表现了地震波复杂的周期成分。随着时间增长,三分量的穿零率呈减小趋势;随着震中距增加,三分量的穿零次数明显增多,即地震波的振动幅度随着震中距增大呈减小趋势,且振动频率随震中距增大而增快。同时可见,震中距越大,穿零率随着时间的衰减越慢。
3.2 穿零率拟合曲线变化
由上节分析与图示可知,地震波穿零率成分复杂,以最简洁的线性拟合来描述穿零曲线特性,可清晰直观了解穿零曲线的相关特性。
图7a~d代表了三分量的穿零率在不同震中距条件下随着时间增长的衰减变化。总体而言,竖直分量记录的穿零率大于水平分量的穿零率,可见竖直分量加速度记录中高频成分更多一些,此外,竖直分量的穿零率随时间的衰减最慢,水平分量的穿零率衰减速度相差不大。
4 结论
本文以2014年8月3日云南鲁甸6.5级地震中的58组强震动记录为基础,详尽分析了相对峰值持时随震中距的变化规律,并按不同震中距分布统计研究穿零率的特性,以此了解本次强震动频率的非平稳性。研究表明,云南鲁甸6.5级地震动频率非平稳性有以下特征:
(1)三分量的相对峰值持时水平分量的离散性大于竖直分量的离散性,持时随着震中距的变化,整体上是离散分布于0秒至45秒范围内,且持时随着震中距增大而增大。
(2)随着时间增长,三分量的穿零率呈减小趋势;随着震中距增大,三分量的穿零次数也明显增长,即地震波的振动幅度随着震中距增大呈减小趋势,振动频率随着震中距增大而速度增快。同时可见,震中距越大,地震动所包含的低频成分越多,且随着震中距增大,穿零率随着时间的衰减逐渐减慢。
(3)竖直分量记录的穿零率大于水平分量,且竖直分量的穿零率随时间的衰减最慢,水平分量的穿零率衰减速度相差不大。
参考文献:
董娣,周锡元,徐国栋等.2006.强震记录频率非平稳特性的若干研究.地震工程与工程振动,26(1):22-29.
李英民,赖明,白绍良.2000.三维地震动频率非平稳特性的相关性研究.重庆建筑大学学报,22(增刊1):22-26.
廖振鹏.1994.强烈地震地面运行模拟.北京:地震出版社.
卢大伟,李小军.2010.中国大陆强震动观测发展研究.国际地震动态,(10):35-42.
王国权,周锡元,马宗晋等.2001.921台湾地震近断层强地面运动的周期和幅值特性.工程抗震,(1):30-36.
王国权,周锡元.2003.台湾集集地震近断层强震地面运动加速度时程的随机特性.防灾减灾工程学报,23(4):10-19.
王君杰,周晶.1997.地震动频谱平稳性对结构非线性反应的影响.地震工程与工程振动,17(2):16-20.
谢俊举,温增平,高孟潭等.2011.2008年汶川地震近断层地震动的非平稳特征.地球物理学报,54(3):728-736.
谢礼立,周雍年.1984.一个新的地震动持续时间定义.地震工程与工程振动,4(2):27-35.
杨黎薇,邱志刚,崔建文等.2016.2014年景谷6.6级强地震动频率非平稳特性研究.北京:强震动观测与应用研讨会论文集,68-82.
赵凤新,胡聿贤.1994.地震动非平稳性与幅值谱和相位差谱的关系.地震工程与工程振动,14(2):1-6.
赵艳,郭明珠,季杨等.2007.场地条件对地震动持时的影响.震灾防御技术,2(4):417-424.

