初中数学习题改编的策略分析

    谢培培

    

    

    

    [摘? 要] 初中数学教师要善于对现有习题资源进行改编，以为学生创造更好的练习体验，提升他们的练习效果. 文章结合具体实例指出，教师可以从条件、结论和背景三个角度出发，对习题进行改编，同时强调教师在改编的过程中一定要兼顾到学生的学习情况，以让改编的习题更加匹配学生的发展需要.

    [关键词] 初中数学;习题改编;基本策略

    在初中数学教学中，教师经常需要提供一些习题来帮助学生对所学内容进行巩固，这些习题可以是教师直接选编过来的，也可以是改编或创编的. 无论是选编现成的题目，还是改编或创编，都在考验初中数学教师的教学基本功. 其中，改编的题目尤其值得教师关注. 因为改编大多是在一些典型例题或中考试题的基础上进行的，这一操作在变式教学中也经常被用到，如果学生有意识地对原题和改编题进行比较，将有助于他们提升认识，强化理解.

    教师在对习题进行改编时，需要将原有问题分解为条件与结论两部分，然后通过对条件、结论或问题背景进行改编或重新设计，由此得到一个新的问题. 这样改编出来的问题更接近学生的最近发展区，更有助于学生从陌生过渡到熟悉，能有效激起他们的思维，能让学生在分析中获得发展.

    对于某些典型的数学问题，教师可着手对它的条件进行分析，并对其展开调整，这样就能演变成一个新的问题. 这样处理可以让学生展开比较——虽然新的问题和原有习题之间存在着很大的相似性，但最终却会得到截然不同的结论. 这样的处理方式会让学生认识到数学问题的多变性，他们的思维也将因此变得更加灵活[1].

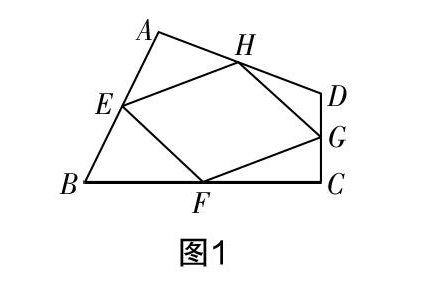
    例1 现有一个如图1所示的四边形ABCD，其中AB，BC，CD，DA四边的中点分别为E，F，G，H. 求证：顺次连接上述中点，所得的四边形EFGH是一个平行四边形.

    上述问题是一个有关四边形和中位线的典型例题，它为学生后面学习矩形、菱形以及正方形等知识奠定了基础. 在教学过程中，很多教师没有充分发掘这个问题的隐含功能，只是安排学生通过连接对角线来完成对问题的处理，这其实在一定程度上增强了问题的特殊性. 这虽然也能帮助学生训练有关中位线和平行四边形的相关认识，但笔者认为还没能让学生能力的提升达到应有的程度. 因此，笔者对上述试题进行了以下改编尝试.

    改编1 如果E，F，G，H四个点并非原四边形各边的中点，那么是否可以让四边形EFGH仍然是一个平行四边形？

    改编2 在改编1的条件下，是否可以让四边形EFGH成为一个菱形？

    改编3 能否在四边形ABCD四条边上找到四个点E，F，G，H，让它们都不是对应边的中点，且连线也与AC，BC不平行，但是四边形EFGH仍然是一个平行四边形？

    改编4 在改编3的条件下，是否可以让四边形EFGH成为一个菱形？

    在改编操作中，教师应有意识地增强条件或弱化条件，将原来的问题成功转化为一个新的问题，这能促进学生对原来的数学问题进行更进一步的引申思考和推广思考，进而让学生以更加积极的姿态参与到学习之中. 同时，他们也将在问题解决的过程中发展自己的探究能力与合作学习精神.

    一个相同的问题场景，如果教师能够切换观察的视角，同时适当对相关数据进行微调，就很有可能促进问题的演变，并得到完全不同的结论. 按照这样的思路对问题进行重新设定或改编，能让学生的视野更加开阔[2].

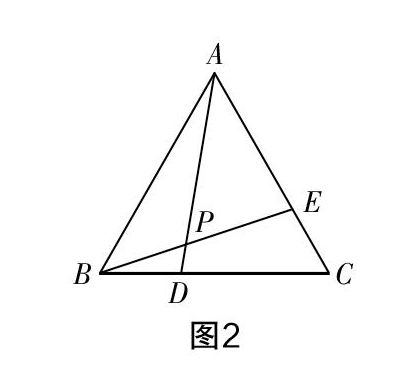
    例2 在如图2所示的等边三角形ABC中，点D在BC边上，点E在AC边上，且AE=CD，连接AD和BE，它们相交于点P，求证：∠APE=60°.

    上述例题是一个相当经典的问题，很多教师都是围绕着图形中的两组全等三角形来展开情境探索并设计问题的. 如果我们的视野再开阔一点，所能捕捉到的相似三角形一共会是六对，笔者从这一思路出发，对问题进行了改编.

    改编 在如图2所示的等边三角形ABC中，AB=6，点D在BC边上，点E在AC边上，且AE=CD=4. 连接AD，BE，它们相交于点P.

    （1）求证：△ABE≌△CAD;

    （2）求EP的长.

    这道改编题虽然简短，但容量很大，它将三线合一、勾股定理、全等三角形、相似三角形等知识整合到了一起，有助于学生完成对知识的融会贯通. 为了匹配学生的差异性，笔者在进行问题改编时，也注意了问题的梯度设计. 上述问题（1）的设计就相对简单，同时这也在一定程度上为学生的后续问题探讨奠定了基础. 问题（2）的难度有所提高，为部分优秀学生提供了展示的平台，有助于学生在深入探索情境中发现更加深刻的數学知识. 这样的处理方式，能对学生思维的变通性展开有效训练，能让学生以更加灵活的视角研究和分析相应的问题场景，这对学生思维品质的提升大有益处，值得我们在教学实践中大力推广.

    很多数学问题都是纯粹的字母或算式，这会给人一种非常抽象的感觉，而且这种过分模型化的问题其实也剥夺了学生展开建模思考的机会. 因此，面对一些问题，教师应该对问题背景进行适当调整，给习题一个更加丰满的情境，这样便可以让数学问题更加有内涵，还能让学生的研究和探索能力因此得到提升[3].

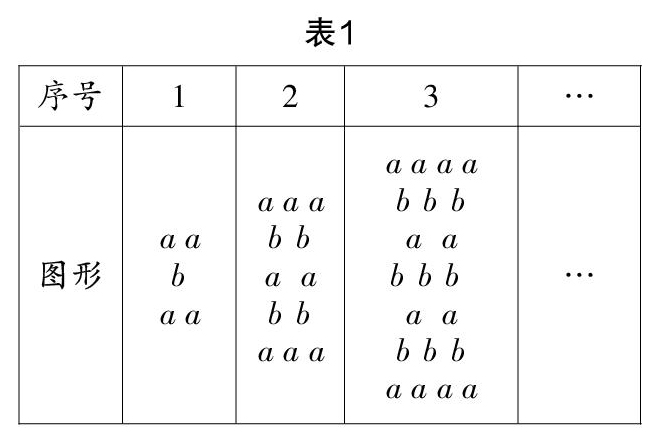
    例3 观察以下多项式：4a+b，8a+4b，12a+9b，16a+16b…请推测第n个多项式应该怎样表示.

    上述问题的难度并不大，只是让学生从现有多项式的层面来寻找规律，这样的问题如果直接安排学生处理，笔者认为缺乏新鲜感与层次感，因此笔者在对上述问题进行改编时，就对问题的背景进行了调整，将其改编成了三个层次，由此演变成有关规律探索、方程分析和函数研究等方面的问题. 这样的处理方式能最大限度地激活学生的思维，能让学生以更加饱满的热情参与到问题研究的过程之中.

    我们将每一个格子中的多项式作为特征多项式，比如，第1格可以表示为4a+b. 请回答以下问题.

    （1）第3格所对应的特征多项式怎样表示？第4格所对应的特征多项式怎样表示？第n格所对应的特征多项式怎样表示？

    （2）如果第1格对应的特征多项式等于-10，第2格对应的特征多项式等于-16，请据此确定a和b的值.

    （3）在问题（2）的条件下，第n格所对应的特征多项式存在最小值吗？如果存在，请确定n的取值;如果不存在，请简述理由.

    设计上述改编题时，笔者以新定义的方式来进行设计，这能给学生营造一种耳目一新的感觉，而且这个问题的起点相对较低，还具有非常明显的梯度，所以非常适合学生逐步提升数学水平. 这与当前中考试卷强调能力立意的基本思想相吻合，其还是坚持以生为本，立足学生发展教育理念的体现. 教师在进行改编时，要充分考虑学生的实际需要，要让每一个问题都具有一定的启发性和引导性，要让学生在问题分析中能得到有效提升和发展.

    试题命制是教师非常重要的一项专业素养，但对于教师而言，如果要全新地命制一个数学问题，还是存在一定困难的. 在实际教学中，教师要积极研究已有试题资源的类型和特点，有效联系学生的实际情况和发展需要，发掘相关问题的潜在价值，进而探索问题改编的思路，让问题以更新、更活的形式展现在学生面前，让习题成为学生巩固认识的支架，让习题成为学生推进数学探究的出发点.

    参考文献：

    [1]李小兵. 挖掘习题内涵? 探究问题真谛—— 一道课本习题的改编历程[J]. 中学数学教学参考，2013（8）.

    [2]柳艳秋. 设计源于“轻负”，改编呈现“高质”——谈“轻负高质”下的高中数学例题设计[J]. 数学教学通讯，2017（30）.

    [3]陈波. 改编习题注重关联，系统开发引领思考——以“勾股定理”相关编题为例[J]. 中学数学，2016（8）.