巧妙过渡，深入探究

    吴金平

    

    [摘? 要] 恰当的过渡性语言能使数学各章节之间的联系更加顺畅而紧密，能使学生在前后贯穿的知识联系中拾阶而上并形成深入的思考. 因此，教师应根据具体的教学内容与学生实际情况，设计恰当的过渡性语言，以促进学生的学习活动顺利展开.

    [关键词] 环节;过渡;过渡性语言;探究

    数学教学中各个环节之间的过渡都需要恰当的过渡性语言来连接，严谨而又系统的数学知识的各章节之间都是前后贯穿且相互联系的，所以教师在具体的教学中应掌握知识之间的联系，并设计恰当的过渡性语言，以促进学生的学习活动有效展开.

    顺学而导地让学生在新知识的接触之中逐步走向更深处，需要教师着眼于学生已有知识与经验，从而做出合理的预设. 而完善的过渡性语言是各知识环节顺利串联所必需的. 因此，教师应根据教学内容与学生实际，建立助引政策，并推进学生深入思考，使学生能够在更为广阔的思考空间内深刻掌握新的知识.

    案例1 “矩形”的教学.

    第一环节：平行四边形的定义与性质的回顾.

    第二环节：矩形性质的学习.

    师：大家觉得矩形是不是平行四边形呢？

    生1：是.

    师：那它是否具备平行四边形的性质呢？

    生2：是的.

    师：很好，它是特殊的平行四边形. 那么，除了平行四边形的性质以外，大家可曾想过它还具有哪些比较独特的性质呢？

    生3：它的四个角都是直角.

    师：理由是什么？

    生4：根据平行四边形的对角相等和邻角互补可以得出矩形的四个角都为直角.

    （教师在矩形图上标上了直角符号并板书性质1）

    师：这一性质其实我们在小学就已经学过，那它还有其他性质吗？

    （教室顿时安静了下来，有的学生开始在课本中寻找答案）

    师：请大家把书合上，并尝试自己发现.

    （学生们都呆住了）

    师：大家试着想一想，如果将矩形的对角线连接起来，它们的大小关系是怎样的？

    生5：相等.

    师：怎样证明矩形的对角线相等呢？

    （教师引导学生探寻证明方法的同时，板书了性质2）

    评析 教师在此案例中运用了“矩形是不是平行四边形呢”“大家可曾想过它还具有哪些比较独特的性质呢”等过渡性语言，将学生的思维引向矩形性质的探究. 但这看似流畅且符合学生认知发展的教学却没有起到激活学生思维的作用，甚至教师在学生探究不能深入之時，只能自圆其说. 那这种“冷场”现象是怎么出现的呢？从过渡性语言设计的角度进行回顾与分析不难发现以下问题：（1）缺乏有效性. 此案例所设计的问题只需要学生简单地回答“是”或“不是”，这种简单的呈现令过渡性语言本应具备的价值荡然无存. （2）缺乏思维含量. “如果将矩形的对角线连接起来，它们的大小关系是怎样的”，这种问题直接指向答案，学生的思考空间不足，自然无法产生探究新知的欲望.

    由此可见，两环节之间过渡性语言的设计也是很有讲究的，教师应把握教学对象的重难点进行有意义的设计. 矩形性质中重要的研究对象、性质研究的途径与方法是教师在过渡性语言设计中应该突出与关注的两个方面.

    优化设计 ? 平行四边形的定义与性质的共同回顾.

    师：大家还记得我们研究平行四边形的性质时是从哪些方面入手的吗？

    生1：边、角、对角线.

    师：矩形之所以是特殊的平行四边形，正是在于其角的特殊. 那么这一特殊性是否会令矩形具备不同的特性呢？

    生2：它的四个角均为直角.

    师：如果我们也从边、对角线的角度上来研究，是否会有新的发现呢？

    （引导学生作图并画出两条对角线）

    生3：边没有特别的，不过其对角线互相平分且相等.

    师：你是如何发现的呢？

    评析 学生在教师的过渡性语言引导下，按照角、边、对角线的顺序进行研究. 着眼于矩形和平行四边形的不同点所进行的类比探究，能让学生很好地积累学习方法与经验. 指向研究方法的过渡性语言设计能让学生在推理、归纳、演绎中获得新的知识.

    学生在前面环节中获得的知识技能与活动经验，会对后面环节的学习产生直接的影响. 但学生在前面环节中所产生的元认知很有可能存在错误的信息，因此，教师应设计具备启发性与提示性的过渡性语言，以帮助学生形成正确的认知或拨乱反正. 教师在处理学生认知上的错误信息时，可以首先进行点拨，使学生明了错误信息中需要思考的地方，并引导学生逐步转换，最终形成正确的思维.

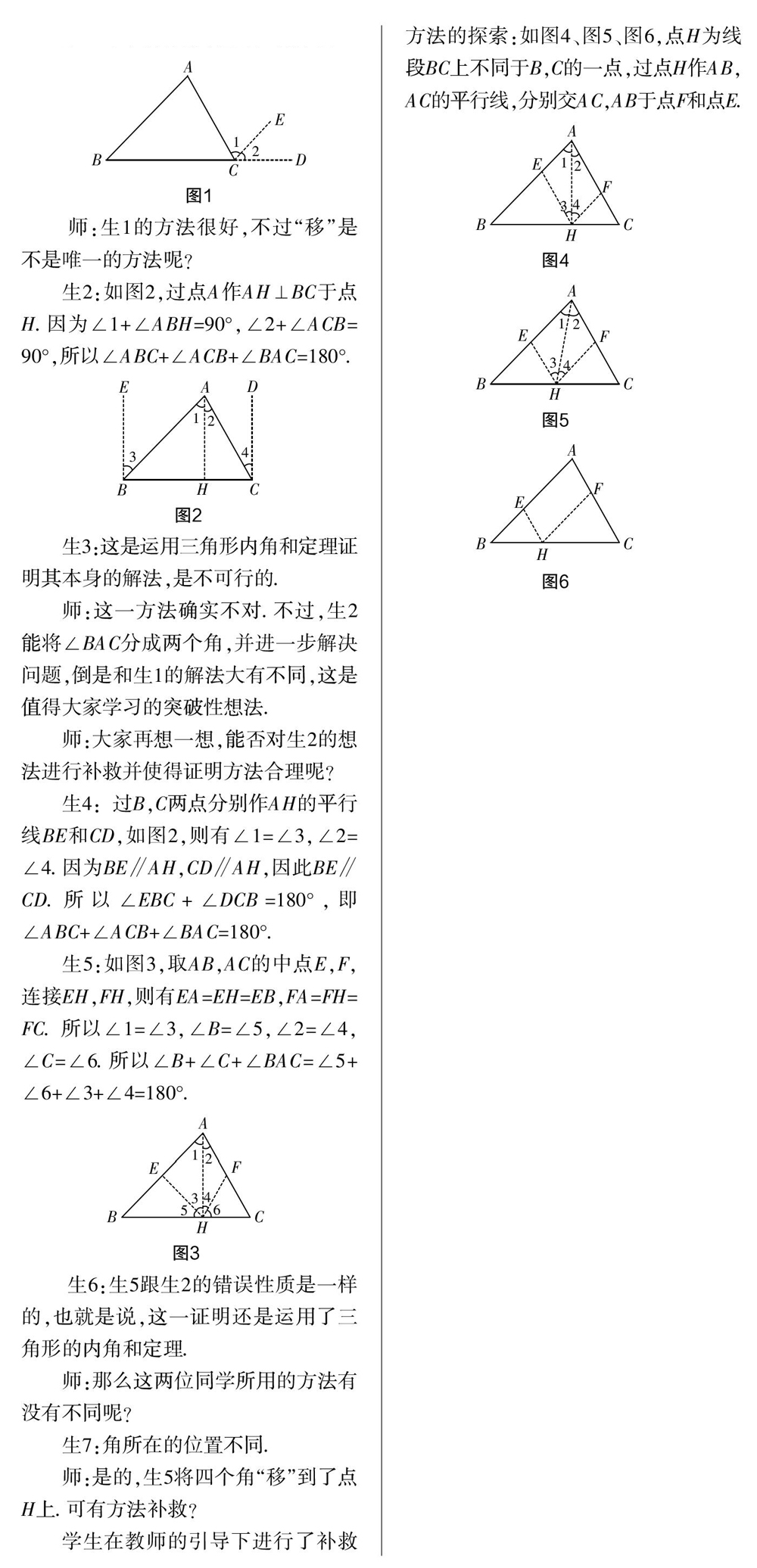
    案例2? “三角形内角和定理证明”的教学.

    学生知识、经验、方法的局限令其在三角形内角和定理的证明中出错是很正常的，这是学生思维本真的体现. 教师可以在学生进行自我否定、自我纠错的过程中进行恰当的过渡性语言设计，使过渡性语言能够在这一过程中充分发挥润滑剂、催生剂的作用. 如上述过渡性语言便突出了以下两个方面，起到了催生剂的作用：

    （1）突出认知过程. 运用补救证明方法这一过渡性的语言引导学生经历有中生错、错中生错、错中生疑、疑中生有的过程，能丰富学生知识素材的同时，为学生的纠错创造更加广阔的思考天地，使学生能够在纠错中充分体验思维发散的合理性与多向性.

    （2）凸显解题方法. 从补救证明方法到研究两位学生证法上的区别，再到“移”的方法上的考量，一步一步的过渡性语言将教学对象的两个教学点在方法纠错中很好地凸显了出来，证明方法的基本思想和证明含义的理解都在逐步过渡中凸显了出来. 学生不仅领悟了抓不变这一数学解题的根本，还在变与不变中对问题形成了更加清醒的认识，获得了处理的办法. 学生对“题设”“结论”关系上的认知不明，导致其对定理证明的因果关系无法很好地确立，但方法的纠错令学生对“证明”的意义建立了更好的理解，证明的步骤与应用也在此基础上获得了完善.