2018年全国高考数学“概率统计”试题分析及教学思考
项丽红 逯彦周

【摘 要】 ?通过对2018年全国高考数学“概率统计”试题的统计分析,发现试题对于概率统计知识的考查主要集中在基础知识上,绝大部分题目难度低,考纲中要求的知识点大部分被覆盖;以数学史料为引子,考查数学思想方法;将问题设置在一定情境中考查数学核心素养;将概率统计知识与其他知识相结合考查应用、创新意识,并以此为依据提出了相应的教学建议.
【关键词】 ?2018年高考;概率统计;试题分析;教学思考
统计是研究如何合理收集、整理、分析数据的学科,概率是研究随机现象规律的科学,概率的概念是数据分析的理论基础,贯穿数据分析的整个过程,是数据分析各阶段的思想基础 [1].高中阶段的概率统计知识不仅是高中数学课程内容的重要组成部分,同时也是大学概率统计学习的基础,起到承上启下的作用.本文对2018年全国高考数学试卷中的概率统计试题进行统计分析,并对教师教学给出几点建议.
1 高考试卷考查“概率统计”知识的试题统计
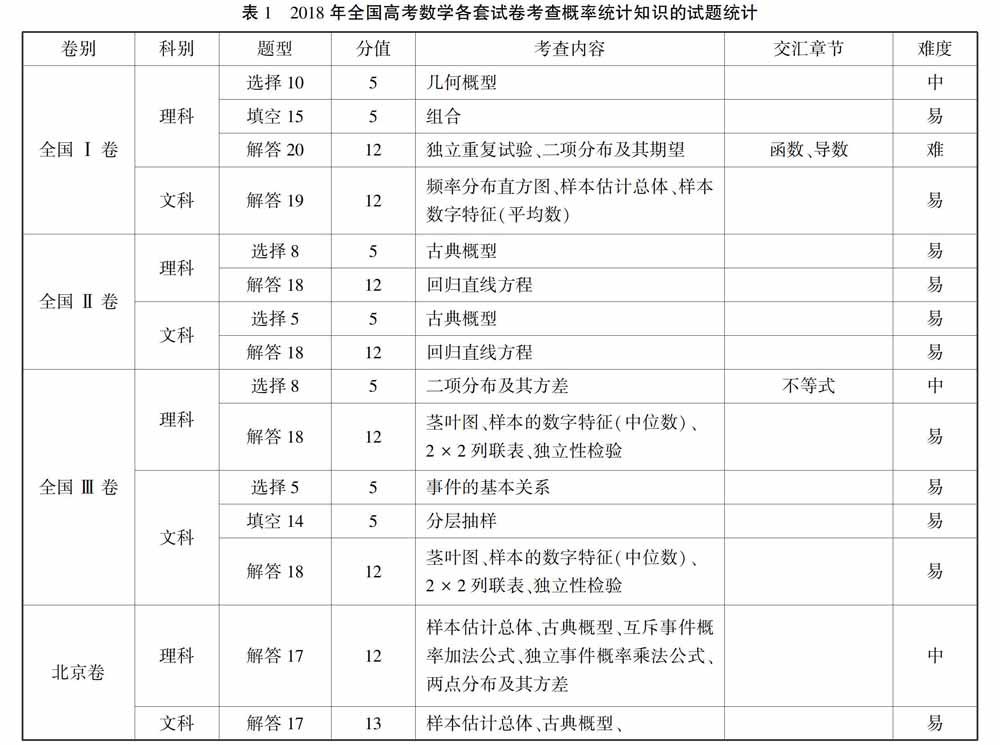
2018年全国高考数学文、理科试卷共13套,其中全国卷6套(分别为全国Ⅰ、Ⅱ、Ⅲ卷文、理各1套),自主命题卷7套(分别为北京卷、天津卷文、理各1套,上海卷、江苏卷、浙江卷不分文理各1套),均对概率统计知识进行了考查,共计23题.现将13套试卷中考查概率统计知识的试题按照题型、分值、考查内容、交汇章节及难度进行统计,结果如表1所示.[FL)]
由表1知,从题型、分值看,全国卷Ⅰ卷文1道解答题,分值为12分,占试卷总分的8.0%;全国Ⅰ卷理选择、填空、解答题各1道,分值为22分,占试卷总分的14.7%;全国Ⅱ卷文、理选择、解答题各1道,分值为17分,占试卷总分的11.3%;全国Ⅲ卷理选择、解答题各1道,分值为17分,占试卷总分的 11.3%,文选择、填空、解答题各1道,分值为22分,占试卷总分的14.7%;北京卷文、理各1道解答题,分值分别为13、12分,占试卷总分的8.7%、8.0%;天津卷文、理各1道解答题,分值均为13分,占试卷总分的8.7%;上海卷2道选择题,江苏卷2道填空题,分值均为10分,占试卷总分的6.7%;浙江卷选择、填空题各1道,分值为8分,占试卷总分的5.3%.
从考查内容看,13套试卷对概率统计知识的考查涉及几何概型、古典概型、频率分布直方图、样本估计总体、样本数字特征(平均数、中位数)、回归直线方程、茎叶图、2×2列联表、独立性检验、分层抽样、列举法计算基本事件数、计数原理、组合、互斥事件概率加法公式、独立事件概率乘法公式、独立重复试验、两点分布及其方差、二项分布及其期望与方差、超几何分布及其期望、离散型随机变量的分布列及方差,内容零碎,覆盖面广.
从难易程度来看,绝大部分试题难度低,但全国Ⅰ、Ⅲ卷理、北京卷理、天津卷理、浙江卷、上海卷中出现中档题,全国Ⅰ卷理出现了较难的题.
2 高考试卷考查“概率统计”知识的试题特点分析
2.1 以经典类型题为主,考查基础知识
试题以考查概率统计内容中的基础知识为主,多为考生在平时训练中所做的经典类型题,如全国Ⅰ卷理15、文19,全国Ⅱ卷文5、文理18,全国Ⅲ卷文14、文理18,北京卷文、理17,天津卷文15、理16,上海卷9,江苏卷3、6,浙江卷16均属于这类题.
例1? (江苏卷6)某兴趣小组有2名男生和3名女生,现从中任选2名学生去参加活动,则恰好选中2名女生的概率为[CD#3].
分析 本题考查基本事件数的求法及古典概型,属于基础题.先算出基本事件数,方法有列举法、树状图法及排列组合法,再用古典概型概率公式得出结果.
2.2 以数学史料为引子,考查数学思想方法
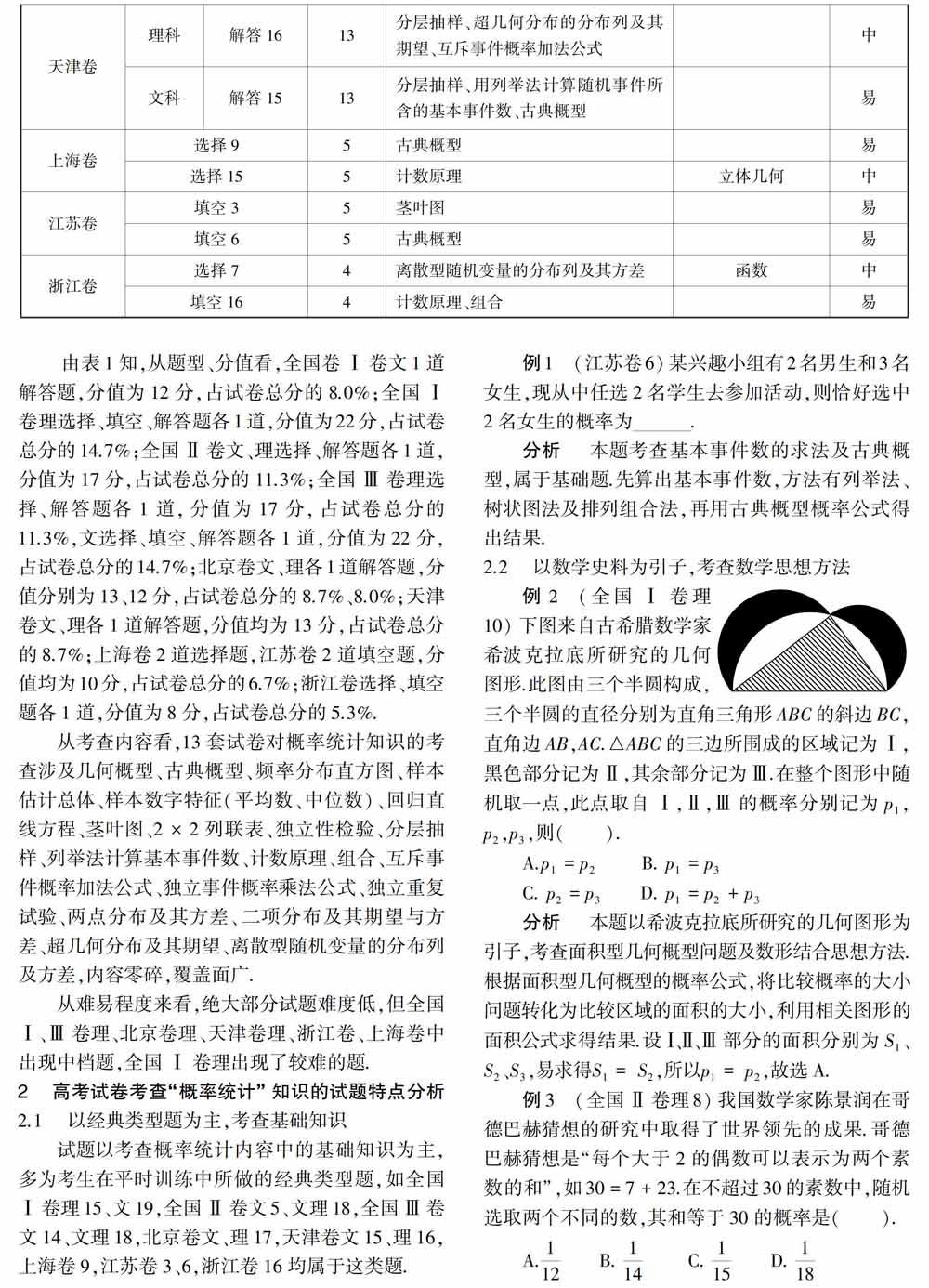
例2 (全國Ⅰ卷理10)下图来自古希腊数学家希波克拉底所研究的几何图形.此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC的斜边BC,直角边AB,AC.△ABC的三边所围成的区域记为Ⅰ,黑色部分记为Ⅱ,其余部分记为Ⅲ.在整个图形中随机取一点,此点取自Ⅰ,Ⅱ,Ⅲ的概率分别记为p1,p2,p3,则(? ).
A.p1=p2 ??B. p1=p3
C. p2=p3? D. p1=p2+p3
分析? 本题以希波克拉底所研究的几何图形为引子,考查面积型几何概型问题及数形结合思想方法.根据面积型几何概型的概率公式,将比较概率的大小问题转化为比较区域的面积的大小,利用相关图形的面积公式求得结果.设Ⅰ、Ⅱ、Ⅲ部分的面积分别为S1、S 2、S 3,易求得 S1= S2,所以 p1= p2,故选A.
例3? (全国Ⅱ卷理8)我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30=7+23.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是(? ).
A. 1 12?? B.? 1 14 ???C.? 1 15?? D.? 1 18
分析 本题以哥德巴赫猜想为引子考查古典概型及分类思想方法.不超过30的素数有10个,随机选取两个不同的数,共有 C 210=45种方法,其中和等于30的选法有3种(7+23=11+19=13+17=30),故概率为 3 45 = 1 15 ,选C.
2.3 以问题情境为载体,考查数学核心素养
概率统计试题几乎都有一定的背景,这些背景就是问题情境,将数学知识融入情境中进行考查,既有利于学生对数学知识的理解,又能体现出对学生学科核心素养的要求.
例4 (北京卷文17)电影公司随机收集了电影的有关数据,经分类整理得到下表:
(Ⅰ)从电影公司收集的电影中随机选取1部,求这部电影是获得好评的第四类电影的概率;
(Ⅱ)随机选取1部电影,估计这部电影没有获得好评的概率;
(Ⅲ)电影公司为增加投资回报,拟改变投资策略,这将导致不同类型电影的好评率发生变化.假设表格中只有两类电影的好评率数据发生变化,那么哪类电影的好评率增加0.1,哪类电影的好评率减少0.1,使得获得好评的电影总部数与样本中的电影总部数的比值达到最大?(只需写出结论)
分析 本题主要考查样本估计总体、古典概型.以电影的好评率为问题情境考查学生的数据分析、数学建模、逻辑推理和数学运算素养,贴近生活.(1)分别计算样本中电影总部数及第四类电影中获得好评的电影部数,代入公式可得概率;(2)利用古典概型公式,计算没有获得好评的电影部数,代入公式可得概率;(3)根据每类电影获得好评的部数做出合理建议.
2.4 以知识融合为新意,考查应用、创新意识
例5? (全国Ⅲ卷理8)某群体中的每位成员使用移动支付的概率都为P,各成员的支付方式相互独立,设X为该群体的10位成员中使用移动支付的人数,DX=2.4,P(X=4)<P(X=6),则P=(? ).
A.0.7?? B. 0.6?? C. 0.4?? D. 0.3
分析 本题主要考查二项分布相关知识,将二项分布的概率与不等式结合,属于中档题.利用公式
D(x)=nP(1-P)
=2.4,得P=0.4或P=0.6,又由P X=4 =C410P4 ?1-P 6<P X=6 =C610P6 ?1-P 4得:P>0.5,故P=0.6,选B.
例6 (全国Ⅰ卷理20)某工厂的某种产品成箱包装,每箱200件,每一箱产品在交付用户之前要对产品作檢验,如检验出不合格品,则更换为合格品.检验时,先从这箱产品中任取20件作检验,再根据检验结果决定是否对余下的所有产品作检验,设每件产品为不合格品的概率都为p(0<p<1),且各件产品是否为不合格品相互独立.
(1)记20件产品中恰有2件不合格品的概率为f(p),求f(p)的最大值点p 0.
(2)现对一箱产品检验了20件,结果恰有2件不合格品,以(1)中确定的p 0作为p的值.已知每件产品的检验费用为2元,若有不合格品进入用户手中,则工厂要对每件不合格品支付25元的赔偿费用.
(ⅰ)若不对该箱余下的产品作检验,这一箱产品的检验费用与赔偿费用的和记为X,求EX;
(ⅱ)以检验费用与赔偿费用和的期望值为决策依据,是否该对这箱余下的所有产品作检验?
分析 本题考查的是有关随机变量的问题,在解题的过程中,一是要明确独立重复试验成功次数对应的概率公式,再者要用函数的思想来研究,应用导数求得其最小值点,在做第(2)问时,需要明确离散型随机变量的可取值以及对应的概率,应用期望公式求得结果,再通过期望的大小关系得到结论.题目将概率与函数、导数相结合,考查学生的应用意识与创新意识以及对知识进行迁移以解决问题的能力,难度较大.
(1)20件产品中恰有2件不合格品的概率为f(p)= C 220 p 2 (1-p) 18.因此 f′(p)= C 220[2p (1-p) 18-18 p 2 (1-p) 17]=2 C 220p (1-p) 17(1-10p).令 f′(p)=0,得p=0.1.当p∈(0,0.1)时, f′(p)>0;当p∈(0.1,1)时, f′(p)<0.所以f(p)的最大值点为 p0=0.1.
(2)由(1)知,p=0.1.
(ⅰ)令Y表示余下的180件产品中的不合格品件数,依题意知Y~B(180,0.1),X=20×2+25Y,即X=40+25Y.所以EX=E(40+25Y)=40+25EY=490.
(ⅱ)如果对余下的产品作检验,则这一箱产品所需要的检验费为400元.由于EX>400,故应该对余下的产品作检验.
3 高中数学“概率统计”教学的若干建议
根据以上分析,不难发现,高考试题对于概率统计知识的考查主要集中在基础知识上,绝大部分题目难度低,考纲中要求的知识点大部分被覆盖;以数学史料为引子,考查数学思想方法;将问题设置在一定情境中考查数学核心素养;另外将概率统计知识与其他知识相结合考查应用、创新意识.因此,在教学中应该:3.1 注重基础知识
2018年高考数学试卷中的概率统计试题,紧扣考纲,考查内容零碎,覆盖面广.虽然题目千变万化,但都以考查基础知识为主.所以在平时教学中,要以课程标准为基准,以教科书为蓝本,紧扣考纲,通过经典类型题进行重点练习,举一反三,打好基础,提高学生应对试题变化的能力.
3.2 重视数学思想方法
日本数学家米山国藏在多年的数学教育中发现,学生在学校所接受的数学知识,毕业后很快会忘记,而唯有头脑中铭记的数学精神及数学的思想方法、研究方法、推理方法等,却能随时随地发挥作用 [2].数学思想具有普遍的指导意义,蕴涵于分析和解决数学问题的过程之中.概率统计知识中蕴含着丰富的数学思想方法,有数学中基本的思想方法,如分类讨论、数形结合、转化化归等,也有概率统计特有的数学思想,如大数定律思想、随机变量思想、抽样思想等 [3].因此在平时教学中,要重视这些数学思想方法的教学,从而提高学生面对不同问题能看破迷雾,抓住本质的能力.
3.3 重视问题情境
合适的的问题情境是考查数学学科核心素养的重要载体 [4].数学源于对现实世界的抽象,与人类和社会发展紧密联系.将数学问题置于一定情境中,不仅能使学生意识到数学与现实世界的联系,还能提升其数学素养,更能使学生学会用数学的眼光看世界,用数学的思维思考世界,用数学的语言表达 世界.
3.4 注重概率统计内容与其他知识的综合性练习
从前面的分析不难发现,高考试卷中的概率统计试题绝大多数难度较低,只有个别题目难度中等或较大,而这些中档题和较难题往往是将概率统计知识与其他知识融合,如与立体几何、不等式、函数、导数结合,以考查学生的应用、创新意识.因此在平时教学中,要注重概率统计内容与其他知识的综合性练习,强化知识之间的融合性,提高学生灵活运用知识的能力,加强其应用、创新意识.
参考文献
[1] 章建跃,宋莉莉,王嵘,周丹.美国高中数学核心概念图[J].课程·教材·教法,2013,33(11):115-121.
[2] 米山国藏. 毛正中,吴素华译.数学的精神思想和方法[M].成都:四川教育出版社,1986.
[3] 邵光华.作为教育任务的数学思想与方法[M].上海:上海教育出版社,2009.
[4] 中华人民共和国教育部.普通高中数学课程标准(2017年版)[M].北京:人民教育出版社,2018.



【摘 要】 ?通过对2018年全国高考数学“概率统计”试题的统计分析,发现试题对于概率统计知识的考查主要集中在基础知识上,绝大部分题目难度低,考纲中要求的知识点大部分被覆盖;以数学史料为引子,考查数学思想方法;将问题设置在一定情境中考查数学核心素养;将概率统计知识与其他知识相结合考查应用、创新意识,并以此为依据提出了相应的教学建议.
【关键词】 ?2018年高考;概率统计;试题分析;教学思考
统计是研究如何合理收集、整理、分析数据的学科,概率是研究随机现象规律的科学,概率的概念是数据分析的理论基础,贯穿数据分析的整个过程,是数据分析各阶段的思想基础 [1].高中阶段的概率统计知识不仅是高中数学课程内容的重要组成部分,同时也是大学概率统计学习的基础,起到承上启下的作用.本文对2018年全国高考数学试卷中的概率统计试题进行统计分析,并对教师教学给出几点建议.
1 高考试卷考查“概率统计”知识的试题统计
2018年全国高考数学文、理科试卷共13套,其中全国卷6套(分别为全国Ⅰ、Ⅱ、Ⅲ卷文、理各1套),自主命题卷7套(分别为北京卷、天津卷文、理各1套,上海卷、江苏卷、浙江卷不分文理各1套),均对概率统计知识进行了考查,共计23题.现将13套试卷中考查概率统计知识的试题按照题型、分值、考查内容、交汇章节及难度进行统计,结果如表1所示.[FL)]
由表1知,从题型、分值看,全国卷Ⅰ卷文1道解答题,分值为12分,占试卷总分的8.0%;全国Ⅰ卷理选择、填空、解答题各1道,分值为22分,占试卷总分的14.7%;全国Ⅱ卷文、理选择、解答题各1道,分值为17分,占试卷总分的11.3%;全国Ⅲ卷理选择、解答题各1道,分值为17分,占试卷总分的 11.3%,文选择、填空、解答题各1道,分值为22分,占试卷总分的14.7%;北京卷文、理各1道解答题,分值分别为13、12分,占试卷总分的8.7%、8.0%;天津卷文、理各1道解答题,分值均为13分,占试卷总分的8.7%;上海卷2道选择题,江苏卷2道填空题,分值均为10分,占试卷总分的6.7%;浙江卷选择、填空题各1道,分值为8分,占试卷总分的5.3%.
从考查内容看,13套试卷对概率统计知识的考查涉及几何概型、古典概型、频率分布直方图、样本估计总体、样本数字特征(平均数、中位数)、回归直线方程、茎叶图、2×2列联表、独立性检验、分层抽样、列举法计算基本事件数、计数原理、组合、互斥事件概率加法公式、独立事件概率乘法公式、独立重复试验、两点分布及其方差、二项分布及其期望与方差、超几何分布及其期望、离散型随机变量的分布列及方差,内容零碎,覆盖面广.
从难易程度来看,绝大部分试题难度低,但全国Ⅰ、Ⅲ卷理、北京卷理、天津卷理、浙江卷、上海卷中出现中档题,全国Ⅰ卷理出现了较难的题.
2 高考试卷考查“概率统计”知识的试题特点分析
2.1 以经典类型题为主,考查基础知识
试题以考查概率统计内容中的基础知识为主,多为考生在平时训练中所做的经典类型题,如全国Ⅰ卷理15、文19,全国Ⅱ卷文5、文理18,全国Ⅲ卷文14、文理18,北京卷文、理17,天津卷文15、理16,上海卷9,江苏卷3、6,浙江卷16均属于这类题.
例1? (江苏卷6)某兴趣小组有2名男生和3名女生,现从中任选2名学生去参加活动,则恰好选中2名女生的概率为[CD#3].
分析 本题考查基本事件数的求法及古典概型,属于基础题.先算出基本事件数,方法有列举法、树状图法及排列组合法,再用古典概型概率公式得出结果.
2.2 以数学史料为引子,考查数学思想方法
例2 (全國Ⅰ卷理10)下图来自古希腊数学家希波克拉底所研究的几何图形.此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC的斜边BC,直角边AB,AC.△ABC的三边所围成的区域记为Ⅰ,黑色部分记为Ⅱ,其余部分记为Ⅲ.在整个图形中随机取一点,此点取自Ⅰ,Ⅱ,Ⅲ的概率分别记为p1,p2,p3,则(? ).
A.p1=p2 ??B. p1=p3
C. p2=p3? D. p1=p2+p3
分析? 本题以希波克拉底所研究的几何图形为引子,考查面积型几何概型问题及数形结合思想方法.根据面积型几何概型的概率公式,将比较概率的大小问题转化为比较区域的面积的大小,利用相关图形的面积公式求得结果.设Ⅰ、Ⅱ、Ⅲ部分的面积分别为S1、S 2、S 3,易求得 S1= S2,所以 p1= p2,故选A.
例3? (全国Ⅱ卷理8)我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30=7+23.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是(? ).
A. 1 12?? B.? 1 14 ???C.? 1 15?? D.? 1 18
分析 本题以哥德巴赫猜想为引子考查古典概型及分类思想方法.不超过30的素数有10个,随机选取两个不同的数,共有 C 210=45种方法,其中和等于30的选法有3种(7+23=11+19=13+17=30),故概率为 3 45 = 1 15 ,选C.
2.3 以问题情境为载体,考查数学核心素养
概率统计试题几乎都有一定的背景,这些背景就是问题情境,将数学知识融入情境中进行考查,既有利于学生对数学知识的理解,又能体现出对学生学科核心素养的要求.
例4 (北京卷文17)电影公司随机收集了电影的有关数据,经分类整理得到下表:
(Ⅰ)从电影公司收集的电影中随机选取1部,求这部电影是获得好评的第四类电影的概率;
(Ⅱ)随机选取1部电影,估计这部电影没有获得好评的概率;
(Ⅲ)电影公司为增加投资回报,拟改变投资策略,这将导致不同类型电影的好评率发生变化.假设表格中只有两类电影的好评率数据发生变化,那么哪类电影的好评率增加0.1,哪类电影的好评率减少0.1,使得获得好评的电影总部数与样本中的电影总部数的比值达到最大?(只需写出结论)
分析 本题主要考查样本估计总体、古典概型.以电影的好评率为问题情境考查学生的数据分析、数学建模、逻辑推理和数学运算素养,贴近生活.(1)分别计算样本中电影总部数及第四类电影中获得好评的电影部数,代入公式可得概率;(2)利用古典概型公式,计算没有获得好评的电影部数,代入公式可得概率;(3)根据每类电影获得好评的部数做出合理建议.
2.4 以知识融合为新意,考查应用、创新意识
例5? (全国Ⅲ卷理8)某群体中的每位成员使用移动支付的概率都为P,各成员的支付方式相互独立,设X为该群体的10位成员中使用移动支付的人数,DX=2.4,P(X=4)<P(X=6),则P=(? ).
A.0.7?? B. 0.6?? C. 0.4?? D. 0.3
分析 本题主要考查二项分布相关知识,将二项分布的概率与不等式结合,属于中档题.利用公式
D(x)=nP(1-P)
=2.4,得P=0.4或P=0.6,又由P X=4 =C410P4 ?1-P 6<P X=6 =C610P6 ?1-P 4得:P>0.5,故P=0.6,选B.
例6 (全国Ⅰ卷理20)某工厂的某种产品成箱包装,每箱200件,每一箱产品在交付用户之前要对产品作檢验,如检验出不合格品,则更换为合格品.检验时,先从这箱产品中任取20件作检验,再根据检验结果决定是否对余下的所有产品作检验,设每件产品为不合格品的概率都为p(0<p<1),且各件产品是否为不合格品相互独立.
(1)记20件产品中恰有2件不合格品的概率为f(p),求f(p)的最大值点p 0.
(2)现对一箱产品检验了20件,结果恰有2件不合格品,以(1)中确定的p 0作为p的值.已知每件产品的检验费用为2元,若有不合格品进入用户手中,则工厂要对每件不合格品支付25元的赔偿费用.
(ⅰ)若不对该箱余下的产品作检验,这一箱产品的检验费用与赔偿费用的和记为X,求EX;
(ⅱ)以检验费用与赔偿费用和的期望值为决策依据,是否该对这箱余下的所有产品作检验?
分析 本题考查的是有关随机变量的问题,在解题的过程中,一是要明确独立重复试验成功次数对应的概率公式,再者要用函数的思想来研究,应用导数求得其最小值点,在做第(2)问时,需要明确离散型随机变量的可取值以及对应的概率,应用期望公式求得结果,再通过期望的大小关系得到结论.题目将概率与函数、导数相结合,考查学生的应用意识与创新意识以及对知识进行迁移以解决问题的能力,难度较大.
(1)20件产品中恰有2件不合格品的概率为f(p)= C 220 p 2 (1-p) 18.因此 f′(p)= C 220[2p (1-p) 18-18 p 2 (1-p) 17]=2 C 220p (1-p) 17(1-10p).令 f′(p)=0,得p=0.1.当p∈(0,0.1)时, f′(p)>0;当p∈(0.1,1)时, f′(p)<0.所以f(p)的最大值点为 p0=0.1.
(2)由(1)知,p=0.1.
(ⅰ)令Y表示余下的180件产品中的不合格品件数,依题意知Y~B(180,0.1),X=20×2+25Y,即X=40+25Y.所以EX=E(40+25Y)=40+25EY=490.
(ⅱ)如果对余下的产品作检验,则这一箱产品所需要的检验费为400元.由于EX>400,故应该对余下的产品作检验.
3 高中数学“概率统计”教学的若干建议
根据以上分析,不难发现,高考试题对于概率统计知识的考查主要集中在基础知识上,绝大部分题目难度低,考纲中要求的知识点大部分被覆盖;以数学史料为引子,考查数学思想方法;将问题设置在一定情境中考查数学核心素养;另外将概率统计知识与其他知识相结合考查应用、创新意识.因此,在教学中应该:3.1 注重基础知识
2018年高考数学试卷中的概率统计试题,紧扣考纲,考查内容零碎,覆盖面广.虽然题目千变万化,但都以考查基础知识为主.所以在平时教学中,要以课程标准为基准,以教科书为蓝本,紧扣考纲,通过经典类型题进行重点练习,举一反三,打好基础,提高学生应对试题变化的能力.
3.2 重视数学思想方法
日本数学家米山国藏在多年的数学教育中发现,学生在学校所接受的数学知识,毕业后很快会忘记,而唯有头脑中铭记的数学精神及数学的思想方法、研究方法、推理方法等,却能随时随地发挥作用 [2].数学思想具有普遍的指导意义,蕴涵于分析和解决数学问题的过程之中.概率统计知识中蕴含着丰富的数学思想方法,有数学中基本的思想方法,如分类讨论、数形结合、转化化归等,也有概率统计特有的数学思想,如大数定律思想、随机变量思想、抽样思想等 [3].因此在平时教学中,要重视这些数学思想方法的教学,从而提高学生面对不同问题能看破迷雾,抓住本质的能力.
3.3 重视问题情境
合适的的问题情境是考查数学学科核心素养的重要载体 [4].数学源于对现实世界的抽象,与人类和社会发展紧密联系.将数学问题置于一定情境中,不仅能使学生意识到数学与现实世界的联系,还能提升其数学素养,更能使学生学会用数学的眼光看世界,用数学的思维思考世界,用数学的语言表达 世界.
3.4 注重概率统计内容与其他知识的综合性练习
从前面的分析不难发现,高考试卷中的概率统计试题绝大多数难度较低,只有个别题目难度中等或较大,而这些中档题和较难题往往是将概率统计知识与其他知识融合,如与立体几何、不等式、函数、导数结合,以考查学生的应用、创新意识.因此在平时教学中,要注重概率统计内容与其他知识的综合性练习,强化知识之间的融合性,提高学生灵活运用知识的能力,加强其应用、创新意识.
参考文献
[1] 章建跃,宋莉莉,王嵘,周丹.美国高中数学核心概念图[J].课程·教材·教法,2013,33(11):115-121.
[2] 米山国藏. 毛正中,吴素华译.数学的精神思想和方法[M].成都:四川教育出版社,1986.
[3] 邵光华.作为教育任务的数学思想与方法[M].上海:上海教育出版社,2009.
[4] 中华人民共和国教育部.普通高中数学课程标准(2017年版)[M].北京:人民教育出版社,2018.

