从“弱水三千”到“何取此瓢”

    郑瑞 杨一丽

    

    

    

    2019年宁波市中考数学第26题，从题材构思到最终定稿，经历了一个从“弱水三千”到“只取一瓢”的过程，可何取此瓢？历经千番.现将命制的主要过程及思考与大家分享.

    1 试题呈现

    如图1，⊙O经过等边△ABC的顶点A，C（圆心O在△ABC内），分别与AB，CB的延长线交于点D，E，连结DE，BF⊥EC交AE于点F

    图1 图2

    （1）求证：BD=BE;

    （2）当AF∶EF=3∶2，AC=6时，求AE的长;

    （3）设AFEF=x，tan∠DAE=y

    ①求y关于x的函数表达式;

    ②如图2，连结OF，OB，若△AEC的面积是△OFB面积的10倍，求y的值

    简解 （1）易证∠DEB=∠BAC=∠C=∠D，则BD=BE.图3

    （2）如图3，过点A作AG⊥EC于点G，

    则BG=3，AG=33，

    易得BGEB=AFEF=32，所以BE=2，即EG=5，

    所以AE=（33）2+52=213

    （3）①如图3，过点E作EH⊥AD于点H.设BE=a，

    则EH=32a，BH=12a.

    因为BGEB=AFEF=x，所以BG=ax，则AB=2ax，AH=（2x+12）a.

    所以tan∠EAD=EHAH=32a（2x+12）a=34x+1，即y=34x+1.图4

    ②如图4，过点O作OM⊥EC于点M.设EB=a，

    同①，有CG=BG=ax.

    所以EM=12a+ax，BM=ax-12a.

    因为BF∥AG，

    所以BFAG=BEEG=aa+ax=11+x，

    所以BF=11+xAG=3ax1+x，

    即12×3ax（a+2ax）=10×12×3ax1+x（ax-12a），

    化简得2x2-7x+6=0，解得x1=2，x2=32，所以y=39或37.

    2 命题过程

    2.1 命题立意

    此题为整份试卷最后一题，根据试卷的整体分布和双向细目表，应设计一道以三角形和圆为背景，体现初中数学核心知识点和核心思想的试题，满分14分，难度系数0.35左右.主要立意有以下几条：

    （1）凸显本质.压轴题侧重于关注学生的思维过程，所以它的呈现需要简洁易懂，不能在题干上为难学生，而使其纠缠于题意的“是是非非”.同时为有效遏制题海战术，减轻学生学业负担，试题的命制需要避免模型化，注重通性通法，淡化技巧，体现公平性

    （2）突出核心.试题以特殊三角形、圆、三角函数、相似三角形的基本知识、基本方法为命题的出发点，要求学生在答题中经历观察、推理、计算等基本的数学活动过程，感受几何图形中的内在逻辑关系，体会蕴含的数学思想方法，如從特殊到一般、转化思想、方程思想等，以外显的操作活动发展内隐的数学思维.特别地要与高中的数学知识体系相关联，为学生后续的学习奠定基础，以准确引领一线教学的方向

    （3）体现功能.问题设置做到起点低，层次分明，让不同的人在数学上得到不同的发展;问题逻辑要连贯，由浅入深，增加试题的区分度，实现对学生应用知识解决问题的能力及综合素养的考查，体现试题的选拔功能.

    2.2 素材研讨

    许多中考试题将三角形内接于圆，通过改变三角形形状，亦或是增添线段，以探究线与角的数量关系和位置关系.我们考虑是否可让圆只过三角形的其中两个顶点？如图1，当⊙O过等边△ABC的顶点A，C时，显然圆心O在AC边的中垂线上运动，△ABE的不确定性和∠OBE的确定性，动中有静，相得益彰，于是命题组开始了尝试.

    2.3 尝试编题图5

    初稿 如图5，等边△ABC的顶点A，C落在⊙O上，延长AB，CB分别交⊙O于点D，E.过点B作BF⊥EC交AE于点F.设AFEF=x，tan∠EAB=y

    （1）求证：BD=BE;

    （2）求y关于x的函数表达式;

    （3）连结OE，交AB于点P，连结PF并延长交AE于点M，若x=2，AC=4

    ①求⊙O的半径;

    ②在弦AC上找一点N，使得△PMN为直角三角形，求△PMN的面积

    诊断分析：第（1）小题立足基础，为第二问铺垫.可以用圆周角或弧转化，也可以利用三角形全等;第（2）小题求解变量间的关系，关键在于“斜转直”方法的构建;第（3）小题在定量的基础上，巧妙地捕捉到了∠OEA=30°和∠MPE=90°这样两个隐性条件，分别进行设问.综合考查了圆的基本性质（同弧所对圆周角相等，垂径定理），等边三角形，解直角三角形等核心知识的灵活应用，同时注重对符号意识，几何直观，函数思想，分类讨论，数形结合，方程思想的考查.但命题组斟酌后感觉有两点不妥.一是第二问较为抽象，难度偏大，易导致得分率低，同时使学生失去解决后两问的信心.而（3）①的难度不及第二问，且解决思路可以为第二问铺垫，出现逻辑上的“倒挂”.二是不难发现，∠PBF=∠PEA=30°，所以P，F，E，B四点共圆，即∠FPE=∠FBE=90°.此处出现关于点P的相关问题，始终无法避免四点共圆带来的超纲嫌疑.尽管这是一种比较特殊的存在，但只能是“忍痛割爱”，另辟蹊径

    二稿 如图5，（2，3，4稿的第（1）小题均同初稿）

    （2）若x=2，AC=4，求AE的长;

    （3）求y关于x的函数表达式;

    （4）当OF=BF时，求y的值

    诊断分析：此方案第二小题通过数据定量，考查基本的“斜转直”思想方法，以及解三角形的相关知识，并不为难学生，更为重要的是扮演“跳板”的角色，为抽象的第三问做好铺垫;

    第（4）问的设置基于∠FBO=60°的存在，舍去初稿中的点P，把目光着眼于变化的△FBO，承接第（3）问.其亮点在于需要分类讨论点O与点B不重合或者重合两种情况，兼顾思维含量以及数学的严谨性;

    预设解答：当点O与点B不重合时，若OF=BF，则△OFB为等边三角形，即OB=OF.如图6，过点O，A分别作OG，AH垂直于EC.设BE=a，BH=ax，则CE=a+2ax，BG=a+2ax2-a=2ax-a2，所以OB=2ax-a2·23=2ax-a3.而FBAH=EFEA，所以FB=3ax1+x，即2ax-a3=3ax1+x，解得x=3，所以y=2-3.当点O与点B重合时，不难求得x=12，所以y=33

    命题组经过深入思考认为此设问比较单薄，同时所谓的“严谨性”有些“坑人”，虽然类似浙教版八上的中垂线性质定理证明一般，但考场上着实很少有学生能意识到这一点，有悖于试题坚持的“人文关怀”原则，因此我们放弃此设问

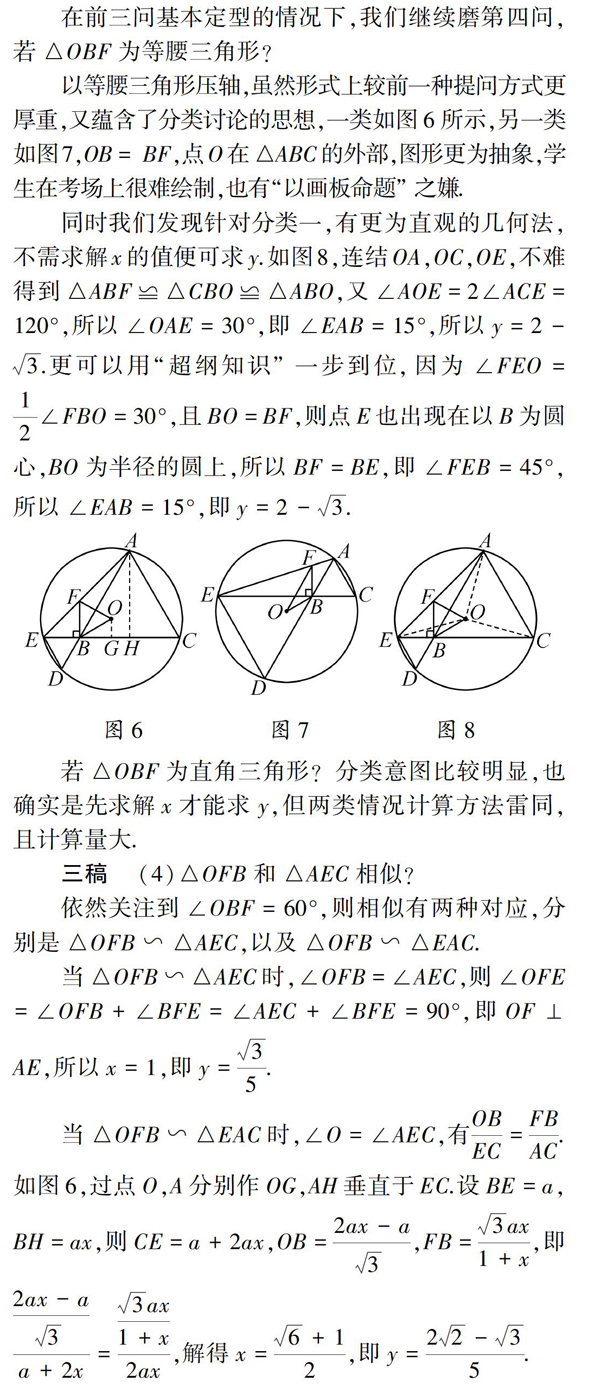
    在前三问基本定型的情况下，我们继续磨第四问，若△OBF为等腰三角形？

    以等腰三角形压轴，虽然形式上较前一种提问方式更厚重，又蕴含了分类讨论的思想，一类如图6所示，另一类如图7，OB=BF，点O在△ABC的外部，图形更为抽象，学生在考场上很难绘制，也有“以画板命题”之嫌

    同时我们发现针对分类一，有更为直观的几何法，不需求解x的值便可求y.如图8，连结OA，OC，OE，不难得到△ABF≌△CBO≌△ABO，又∠AOE=2∠ACE=120°，所以∠OAE=30°，即∠EAB=15°，所以y=2-3.更可以用“超纲知识”一步到位，因为∠FEO=12∠FBO=30°，且BO=BF，则点E也出现在以B为圆心，BO为半径的圆上，所以BF=BE，即∠FEB=45°，所以∠EAB=15°，即y=2-3图6 图7 图8

    若△OBF为直角三角形？分类意图比较明显，也确实是先求解x才能求y，但两类情况计算方法雷同，且计算量大

    三稿 （4）△OFB和△AEC相似？

    依然关注到∠OBF=60°，则相似有两种对应，分别是△OFB∽△AEC，以及△OFB∽△EAC

    当△OFB∽△AEC时，∠OFB=∠AEC，则∠OFE=∠OFB+∠BFE=∠AEC+∠BFE=90°，即OF⊥AE，所以x=1，即y=35

    当△OFB∽△EAC时，∠O=∠AEC，有OBEC=FBAC.如图6，过点O，A分别作OG，AH垂直于EC.设BE=a，BH=ax，则CE=a+2ax，OB=2ax-a3，FB=3ax1+x，即2ax-a3a+2x=3ax1+x2ax，解得x=6+12，即y=22-35.

    此稿主要考查相似三角形的判定和分類讨论思想，数形结合思想，方程思想等.至此，整题设问相对来说比较满意，各问间关联明显，在思维层次上有了较大提升，突出了对学生数学直观能力，数学抽象，逻辑推理能力，数学运算能力等数学核心素养的考查，体现压轴题考查的效度、信度和区分度.但是如鲠在喉的是，整卷25题新定义试题中已有针对相似三角形的考查，同时基于新课程标准对相似三角形的淡化，以及高中对代数运算能力的需求，命题组斟酌再三，从不定型的两个三角形（△OBF和△AEC）中寻找到了面积之间的一层关联，且上下贯通，数据怡人，犹如破晓前的黑暗中透出了一丝光亮.几番周折，几经打磨，终于达到预设的目标，形成文首呈现的学业考试试题.

    3 思考感悟

    3.1 试题宜简洁

    近几年宁波中考数学卷压轴题都延续着一种风格，在确保试题科学性，规范性，发展性的前提下力争题文简洁，流畅易懂.同时试题蕴含基础知识，体现基本思想，回归数学本真，体现学科素养.

    3.2 导向去模型

    数学建模是中学数学六大核心素养之一，但此处的建模思想更侧重于实际问题建模，有别于几何中的模型.时下的几何教学，部分老师已习惯于经验主义式地让学生记模型，究变式，培养所谓的“举一反三”，加重学生负担.压轴题要体现公平性，必须“去模型化”.要让学生走出题海战术，我们的教学应着重关注学生提出问题、分析问题能力的培养，让数学核心素养落地生根.

    3.3 逻辑重关联

    章建跃先生曾指出，课堂教学要为学生构建逻辑连贯的学习过程.同样的，压轴试题通过多层次设问方式，除了追求逻辑顺畅，也应关注思想方法的连贯性.本题中，第一问对△BDE的关注，第二问对线段长求解，都是为第三问中求解函数表达式所做的铺垫，而高的出现也为面积之比创设了解决之道，一脉相承.?动态几何图形的思考，既是发散联想的，又是收敛循迹的.

    3.4 评价谋发展

    学业考试的目的是全面、准确地反映初中毕业生在初中阶段所达到的水平，也为高中段的招生提供了客观的依据.就目前的高中数学学习而言，学生普遍存在运算能力弱的事实.“童子功”的培养应该始于小学、成于初中.目前的宁波中考，压轴题核心考查学生的直观想象、逻辑推理等数学素养且关注学生的抽象能力、数学运算能力发展的理念，体现积极的初中数学教学导向.本卷压轴题中，压轴问的设计本是“弱水三千”，为何只取那一瓢，其中一个原因也便在于此.