从“大思考”到“大动笔”

    徐超凡

    

    

    

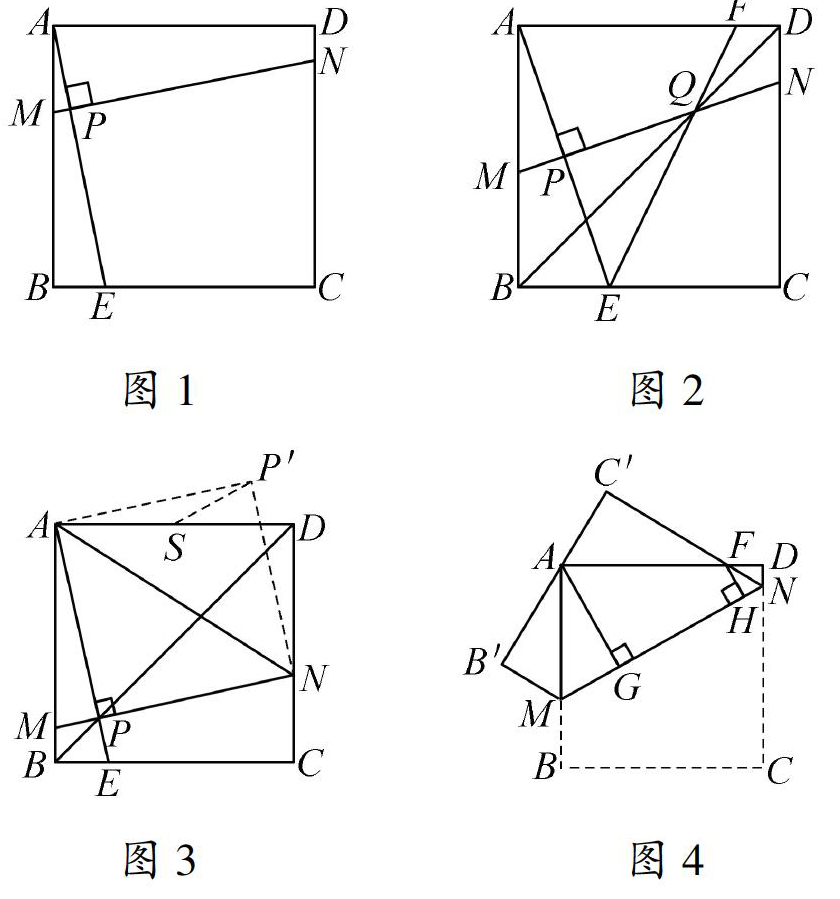
    2019年连云港市中考数学试题第27题，思维含量高，书写量大，辅助量大、变量思想显著，很好地突出了中考试题的选拔功能，有助于不同层次学校的选人和用人，这种“大思考→大动笔”的测查方式，一方面旨在让不同思维水平的学生考出了应有的成绩;另一方面旨在让不同学生在自己的思维水平上“上好学”，尽管，“大思考”到“大动笔”，在一定层面不利于“中段学生”思维水平的精准测查，但不影响对学生思维发展的促进作用。

    1 试题呈现

    2 试题评析

    2019年連云港市中考数学试题第27题考查了正方形的性质、翻折变换的性质、全等三角形的判定和性质、勾股定理、相似三角形的判定与性质、等腰三角形的判定和性质等知识，证明三角形全等和相似是解决问题的关键，

    连云港2019年第27题是对苏科版八年级下册第94页第19题“课本习题”的改编、构造和灵活应用，指导我们要在“做中教数学”，在数学教学层面，要重视学生推理能力的培养，并在提高“思维运演水平”方面要做出进一步努力，通过以上分析，我们发现该题非常重视学生的推理能力和动手操作能力考查，带有强烈的“大思考”“大动笔”特征，教之道在于“度”，学之道在于“悟”，考之道在于“思考”，数学思考是试题的文化精髓和精神长相，是数学考查的重要任务和关键目标，《义务教育数学课程标准（2011年版）》明确指出，在参与观察、实验、猜想、证明、综合实践等数学活动中，发展合情推理和演绎推理能力。清晰地表达自己的想法，这里的“推理”就是一种“大思考”，“表达想法”就是“做数学→大动笔→小动笔”，如何将“大思考”与“大动笔”构筑成一个统一体，并重视“小动笔”书写格局的培养，进而促进学生的数学思维发展呢？

    3 三点思考

    3.1 “大思考”不在于复杂，更在于“大道至简”

    在中考时长定格的心理条件下，大思考不在于复杂，而是简单，这与“观点越高，事物越显得简单”（克莱因语），具有内部关系一致性，中考压轴题是中考试卷的精华，体现了试卷的甄别和选拔功能，但这并不意味着压轴题一定很复杂，难度很大，压轴题一般是依标（课程标准）据本（课本），考查学生的四基：基础知识、基本技能、基本思想、基本活动经验，如果把数学单一的知识比作一块块砖，那么压轴题就是一幢楼，由一块块砖按照一定的规则合理建构而成，由于设计者独具匠心，压轴题风格各异，但扒开现象突出实质，不管它有三十六变还是七十二变，山还是那座山，水还是那湖水，原理还是那原理，连云港市中考数学压轴题以课本习题为母本开花散枝，让学生感到“看似寻常最奇崛，成如容易却艰辛”，其实进行图形分解，逐步将其转化为常见图形，问题就迎刃而解了，为了提高学生解决压轴题的能力，不能一味选择历年中考试卷压轴题编制专题，应该立足教材，展开课本习题教学，在习题的基础上改编，拓展问题，这样做省事省力，让学生学习时刻有成就感，每天进步一点点，久而久之就会迈出一大步，在训练学生思维能力的过程中，不要复杂问题复杂化，而是复杂问题简单化，正如希尔伯特说：“当我听别人讲解某些数学问题时，常觉得很难理解，甚至不可能理解，这时便想，是否可以将问题化简些呢？往往，在终于弄清楚之后，实际上，它只是一个更简单的问题，”比如在学习复杂的几何问题时，一定要归纳方法，注意图形分解，从复杂图形中抽出基本图形（比如相似中的K形图、X形图、A形图），把复杂问题分解为基本知识，化解学生对压轴题的畏难情绪，增强学生解决压轴题的信心。

    课标与教材永远是中考命题的生长点和源头活水，中考数学试题中大约八成的试题来自教材，压轴题也不例外，教材是数学课程标准的直接反映，是基础知识、基本技能、基本思想、基本活动经验的直接载体，教师应该回归教材，在充分理解教材的编写意图、教学要求和教学理念的基础上，从学生的已有经验出发，创设学生熟悉的教学情境，对教学内容适当的整合、补充、加工，创造性的使用教材，发挥教材的示范作用，开发教材中的课程资源，从而衍生一系列创新问题，培养学生的创新思维，为压轴题顺利解决奠定扎实的基础。

    3.2 “大动笔”不在于多写，更在于“道中有道”

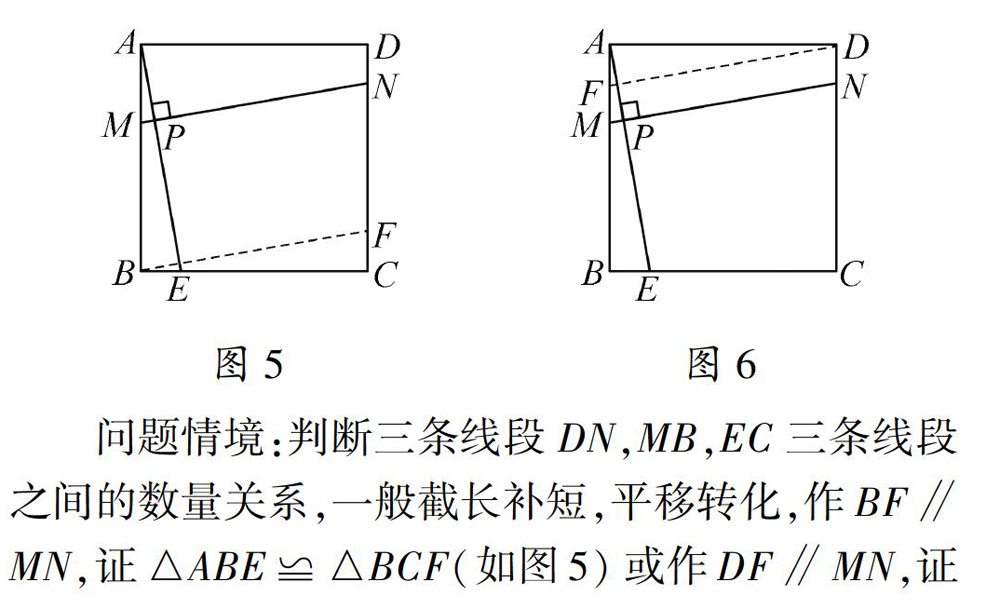
    由于时间限制，在中考考试过程中，如果卷面书写量很大，就会造成不少学生考试不能顺利做完，正如高斯所说“数学中的一些美丽定理具有这样的特性：它们极易从事实中归纳出来，但证明却隐藏的极深，”在解决连云港市中考数学27题问题探究（2）时，由于选择方法不同，书写容量迥然不同，考虑到中考考试时间限制，就要意识到“大动笔”当然不是“写多”和“多写”，重在“言之成理+落笔有据”，教师在日常数学教学中，要避免两种思想导向：一种是数学要多做，做多了，经验自然就有了;一种是解题过程要详细，能写的都写出来，“数学是思维的体操”，数学让人越来越聪明，为此，日常的练习在于精而不在于多。大量的重复练习只会凝固学生的数学思维，把学生的动脑思考搞成体力活，加德纳认为，“数学的真谛就在于不断寻求用越来越简单的方法证明定理和解决数学问题，”教师要求学生在做中提炼方法，对问题归类整理，对于思考容量大的问题，并不是把想到的都要呈现在纸上，思考成果的展示，不能眉毛胡子一把抓，应该把握住关键环节逐一呈现，达到逻辑清晰，言简意赅，一目了然就行了。

    “道中有道”是一种做题思想，一种解题策略，一种数学隋怀，不是一蹴而就的，需要教师严谨的思考态度、科学的表达习惯，思维“留白”的能力，方能让学生在教师的表达方式熏陶下，获得“做道”“生道”能力，因此，我们在教授课本习题时，就要让学生在获得图5中AE=MN直接结果的同时，抛开“就题论题”的不良习惯，延伸思维，让学生进一步获得“EC=BM+DN”的结论，这就是一种“生道”能力，其中，书写的“尚简”能力和“落笔有据”的思想意识就是一种“做道”，为后续预留足够的弹性的思考空间和形成“基本套路”产生式，在笔者看来，好的中考就是在最短的时间内，用最正确的方法、获得最正确的结论，这就是“道中生道”给数学学习带来的最大贡献。

    3.3 “大思考”到“小动笔”，更契合“做中生道”

    “大思考”“大动笔”固然是是中考压轴题的应然追求。但“大思考”到“小动笔”依然是未来中考的一道思维风景线，问题探究（2）中求P'S的最小值，参考答案给出了详细的推理过程，有极大的思考量，不过笔者认为，在考场上，学生很难添加出众多的辅助线，更别说展示极大的书写容量了，卓斯拿斯认为，“纯粹几何学的学说往往会给出，而在许多问题中会给出多个简单而自然的办法来洞察诸真理的来源，去揭露那连接它们的神秘链索，去使它们独特地、明白地、完全地被认识”，为此，求P'S的最小值只需进行数学实验，动手操作，找到点P落点的轨迹，将其转化为点到直线的距离，垂线段最短，通过等腰直角三角形很容易求出P'S的最小值，这样做直观明了，只需小动笔即可解决，就考试而言，得到分数才是硬道理，解答问题时，尽量方法优化，过程简明扼要，为解决下一个疑难问题留下时间多一点，

    在日常的教学中，教师不能只顾埋头拉车，却不抬头望路，要在教的过程中让学生有体悟，不仅仅是悟出方法，更重要的是觉察命题者的思路、意图，及今后侧重学习的方向，回顾一下连云港2017、2018年的中考压轴题，连云港2017年压轴题。考查的是一道四边形综合题，难度比较大，需要添加辅助线，以及利用分类讨论思想，题目相对很长，可能给“场依存”倾向的考生带来一定层面的心理压力，连云港2018年压轴题，考查的仍是四边形、三角形与动点相结合的面积问题，综合性强，第4问，题目篇幅相对2017年来说，有了简化，难度上比2017年有所下降，连云港市连续三年偏爱实验操作题，命题意图非常明显，就是为了推动学生在“做中学数学”，教师在“做中教数学”，进而提升教师的教学水平和学生的思维水平。

    概言之，通過对2019年连云港中考压轴题的分析和思考，旨在培养学生思维能力，启示我们要把发展学生的思维心理水平贯穿在整个数学教学的过程，在实际学习中，一方面，教师要让学生不断地运用比较、分析、综合、抽象、概括、判断、推理等思维方法，建立知识的获得、保持和迁移机制，提高学生的思维能力和思考水平：另一方面，教师要带领学生研究教材、重组教材、用好教材、学好教材，设计具有思考容量的问题。为锻炼学生的思维品质提供具体的内容和载体，让学生感到数学并不陌生，源于课本、高于课本，源于生活，高于生活，进而促进“数学与生活同行”“活动与思考并重”的能力。