基于波谱包络特征的地震事件检测
詹小艳 王恒知 王俊 缪发军 薛莹莹 朱升初

摘要:以声谱图像模式识别为基本思想,改进了基于地震波波谱包络分布特征的初至震相检测方法。改进后的算法,首先将波形记录特征转换为谱能量分布,以台站固有背景噪声的时频特征为基准,提取出记录信号的时频包络特征作为事件触发检测的目标函数。为降低主震尾波对检测后续余震的影响,采用非线性标度缩放因子对大于台站背景噪声水平的能量进行归一化处理。通过2组密集余震序列的实测结果表明:相对STA/LTA算法自动检测结果,新方法正确触发率提高约19.6%,漏触发率则降低了22.6%,表现出更强的抗干扰能力和触发效率,且运行速度快,能够满足地震实时处理系统的技术要求。
关键词:余震序列;初至震相;地震波;波谱能量包络;峰值搜索
中图分类号:P315.3 文献标识码:A 文章编号:1000-0666(2018)02-0258-06
0 引言
完整、可靠的余震序列参数是中强地震发生后或密集震群序列活动时,确定主震发震构造、估计断层破裂尺度、序列后续趋势判定以及开展应急救援等工作关键的基础数据。研究表明,余震序列精定位是确定主震发震构造特征最为有效的途径之一(黄媛等,2008;朱艾斓等,2008):利用余震序列的震源机制解还可以进一步反演震源区构造应力场的分布特征(王勤彩等,2009)。然而,地震学家们通常需要滞后数天甚至更长的时间才能得到有关强余震序列较为完整、可靠的后续研究结果。其主要原因是目前地震实时处理系统所采用的STA/LTA算法对余震序列的检测效率较低,绝大部分余震需要震相分析人员通过查看连续记录波形进行查找。随着台站密度的日益提高,密集余震序列快速检测的数据量也将进一步增加。因此,研究一种快速、高效的地震事件触发检测算法,具有十分重要的现实意义。
自20世纪70年代以来,地震震相的触发检测一直都是国内外学者研究的重点领域,并取得了大量的成果。从最简单的以振幅大小作为触发标准到复杂的图像模式识别、自适应方法、神经网络法以及小波变换的主成分分析法等(Allen,1978;Joswig,1990;Wang,Teng,1995;Witherset al,1998;Patane et al,1999;Sleeman et al,1999;Leonard et al,1999,2000;刘希强等,2000;Massa et al,2006)。这些震相识别方法是根据信号与噪声之间的差异特征而提出,如振幅或能量、频率、波形的相似性、地震波传播方向和动力学特征(如偏振、频谱等),对于单个地震或特定的区域性地震而言,可取得较好效果。但这些复杂、有效的震相触发检测算法,通常由于运算速度较慢而难以满足实时处理的技术要求。
通常情况下,中、强地震发生后短时间内会在震源区附近发生大量的余震,绝大多数余震发震时间间隔极短,甚至相互重叠且处于主震的尾波中。例如,据国家地震台网中心统一编目结果,2008年汶川M8.0地震后50d内,四川地震台网以及应急流动台站共记录到余震总数超过1.6万次,余震最密集时1h内ML>1.0地震达179次;2014年新疆于田M7.3地震后5d内共记录余震总数3294次。尽管震相检测触发方面已有不少研究成果,然而针对地震序列快速监测的研究成果仍然较少。由于STA/LTA算法(短时平均与长时平均值之比)具有算法简单、速度快、便于实时处理等特点(Stevenson,1976),在地震事件的实时触发检测中,国、内外主要地震机构的处理系统仍普遍采用该算法。STA/LTA算法对于环境背景噪声水平低的台站来说非常有效,但它的抗干扰能力不够强,若记录中存在无规则、随机大振幅的干扰信号、或脉冲式噪声以及信噪比较差时,该算法的效率会大大降低。另一方面,在检测过程中,STA/LTA的触发阈值起了决定性的作用,阈值设置得高,小地震则不会触发;而当阈值设置得低时,则会出现大量的误触发。尽管在实际计算过程中有2种方案可供选择,即“锁定”LTA和连续更新LTA,但这2种方法仍有优缺点:“锁定”LTA值使记录系统一直处于触发状态,而连续更新LTA值时,会使尾波过早地被截断(Bor-mann,2006)。此外,采用STA/LTA算法检测余震序列中的初至时,主震尾波及余震之间的相互叠加就成为干扰STA/LTA算法的主要因素。
本文将针对密集余震序列的记录特征,以声谱图像模式识别方法为基本思想,实验一种基于地震波波谱包络分布特征为基础的初至震相快速检测方法,并将其应用于2次地震进行验证。
1 研究方法
Joswing(1990,1993)提出的声谱图像模式识别(Sonogram Pattern Recognition)方法,其基本思想是将各种类型的地震信号与临时噪声信号定义成不同的模式,在实时检测过程中,当与定义模式足够相似时,即被触发,该方法是一种正演的决定逻辑触发模式。触发模式或触发阈值的设置不依赖于地噪声水平,因为它在此阶段对地震信号和突发性噪声采用相同的处理方式。基本步骤为:(1)将记录波形进行非线性化的图像转换,即通过信号的谱能量构建二维灰度图像,其中黑度代表潜能量的密度,在处理过程中采用了非线性的标度缩放因子,使它与简单的谱密度图像有着很大的差异:(2)基于典型的地震信号和噪声建立不同的识别模式。如建立不同类型地震信號与交通、工业噪声、汽车、火车等大幅度噪声之间的模式等;(3)实时检测,即实现检测阈值和最相似模式的逻辑决定。其中(1)、(2)步中构建波形的非线性图像和识别模式难度较大且过程十分复杂,这也是该方法难以被广泛应用的原因所在。
本文是在上述基本思路的基础上,将其改进为波谱能量时频包络线识别模式,基本步骤为:
(1)沿记录波形连续滑动地计算一定窗长内信号的功率密度谱(PSD),在全频段内以1/8倍频为单位间隔计算平均功率谱,即计算在短拐角周期Ts和长拐角周期TL=2×Ts内的平均功率谱值,赋值给几何中心周期Tc[Tc=sqrt(Ts×TL)],记为矩阵Aij:
Aij=psd(fi,tj)(1)式中:fi代表第i个频率,tj代表j时刻的记录波形。
为了最大限度地突出地震信号的能量,同时避开噪声能量最强的频段(Peterson噪声模型中微震峰值频带1~10s),需要在计算前根据不同地震信号(P、S波)的卓越频带范围进行相应的滤波处理。
(2)记录信号的功率谱密度矩阵与该台稳定的噪声功率谱矩阵nij之比,记为Bij:
Bij=Aij/nij(2)式中:nij是根据每个台站背景噪声的功率谱概率密度函数计算得到。对于单个台站的记录,在某一频段内,将信号中高于该台背景噪声功率谱阈值矩阵的部分(即Bij中大于1处),通过非线性的标度缩放因子进行归一化处理,以降低大振幅信号对能量分布权重的影响,换言之,即提高弱信号(尤其是淹没在背景噪声中的信号)在能量分布中的比重。于是可根据高于台站背景噪声水平、归一化后的能量分布和持续时间,提取出地震记录波形在特定频带段内的谱能量时频包络曲线。
(3)通过设定谱能量的触发阈值对信号进行触发检测,这样触发检测就完全取决于台站随频率的噪声水平和各个频点上高于背景噪声水平的持续时间,在持续时间内的信号,即认为是有效的地震信号。
2 实测结果
2.1 江苏高邮M4.9地震余震序列
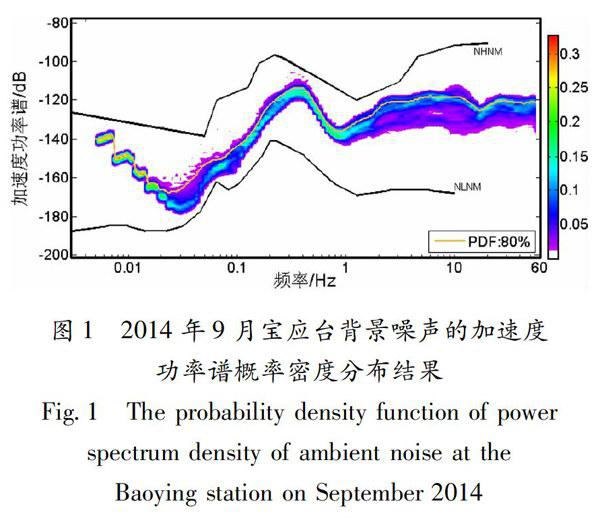
2012年7月20日20时11分,在江苏高邮与宝应交界处发生M4.9地震,这是近30年来江苏省陆地上发生的最大地震。距离主震震中最近的是宝应地震台,震中距约为36.8km。据江蘇省地震台网记录,震后4h内的宝应台共记录余震44次,其中震后1h内的余震为29次(表1)。为验证本文提出的方法,选取了震后1h内的连续记录波形进行回溯性实测。在提取波谱能量包络线之前,先确定被检测台站的各频点上背景噪声水平nij。本文中采用功率谱概率密度函数法计算nij(McNamara,Boaz,2005;王俊等,2009)。取宝应台背景噪声加速度功率谱概率密度函数80%的分布概率代表其背景噪声水平,如图1中黄色线条所示,在1~20Hz频带范围内的平均值约为-145.7dB(噪声水平的有效值约为5.16×10-8m/s)。
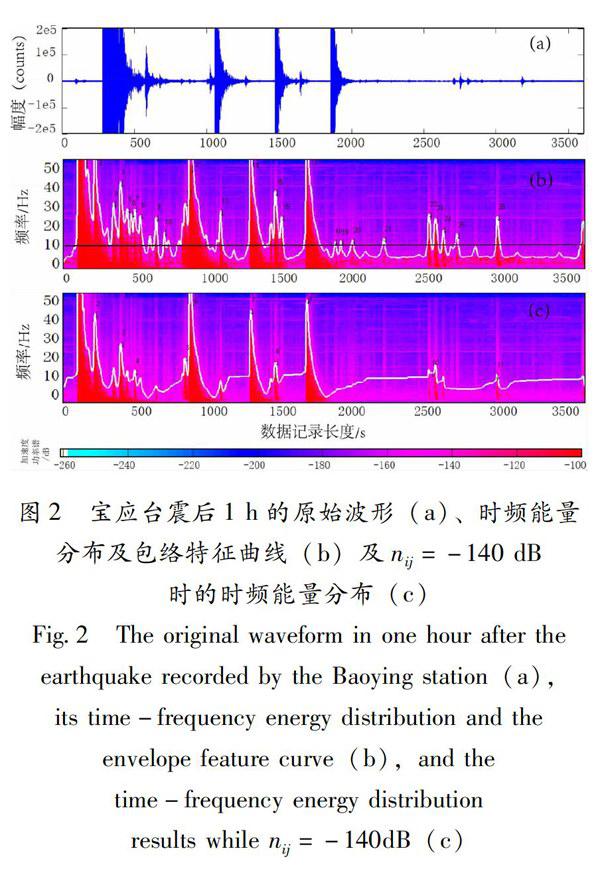
在震中距小于100km的地方震记录中,P波的周期约为0.05~0.2s,同时为避开背景噪声微震峰值的影响,在计算前对连续记录进行1Hz以上的Butterworth高通滤波处理。首先,将垂直向记录波形中高于各频点背景噪声水平的能量进行归一化处理,如图2b中红色区域所示,白色曲线即为根据时频能量分布提取出的特征包络曲线。对比实际记录波形(图2a)可以看出,在经过归一化后的能量包络曲线中,由于大振幅信号在能量分布中的权重被削弱了,除了可以清晰地展现出记录数据中震级较大(ML>3.0)的地震信号外,重叠在主震以及较大余震尾波中的微小余震信号也变得十分清晰,如在主震后600s时间窗内有多组清晰的峰值曲线。如图2c所示,当把台站背景噪声水平nij人为提高5dB时,可以看到记录信号中的大部分余震淹没在背景噪声中,导致无法分辨。这表明记录信号的时频能量特征分布主要取决于记录台站在频域内的背景噪声水平。事实上对于一个固定的地震台站而言,一般情况下背景噪声水平的源是相对稳定的(王俊等,2013)。因此,在准确求得台站的背景噪声水平后,采用以背景噪声水平基准的特征包络曲线来反映记录信号的特征是客观、可靠的。
随后,利用峰值搜索法对时频包络线进行触发检测,具体方法是:在设定的触发能量阈值Fc(图2b中黑色线条)线以上,根据峰值的持续时间(Tc)、坡度(Pc,即峰值的高度除以持续时间的1/2)阈值,进行峰值搜索①。图2b中黑色箭头表示在Fc=10Hz、Tc=20s、Pc=2时的触发情况,除主震外,还检测到29次触发事件。将触发结果与正式编目结果中宝应台的Pg波震相到时进行对比,以检验触发准确率,将触发时间误差在一定范围内的事件视为同一事件,本文中误差取值为2s。由于波谱能量时频包络线法检测到的位置是地震信号中能量分布最强的位置,对于地方震而言它对应的位置一般是S波的振幅最大位置处(图2b,c)。以人工地震编目中Pg震相到时为基准,宝应台实际记录的S-P到时差约为5s,因此将到时误差在4~6s范围内的事件视为同一事件。将准确触发事件数与触发总数之比,定义为准确率;未触发的事件数与实际事件数之比,定义为漏触发率。统计结果显示:采用波谱能量包络方法准确触发的事件共有26次,准确率约为83.4%,漏触发率约10.3%。相比而言,采用STA/LTA算法在触发阈值为3时的常规状态下,共检测出23次,但只有16次触发是有效的,准确触发率约为69.5,漏触发率达44.8%。详细的对应关系见表1。
2.2 新疆和静M6.6地震余震序列
为了进一步验证本文方法,选取1组更为复杂的序列进行实测。2012年6月30日5时7分,在新疆和静(43.4°N,84.8°E)发生M6.6地震,根据新疆地震台网记录结果,震后1h内共记录余震37次,距离震中最近的石场台(SCH台)震中距约为100km。石场台背景噪声的加速度功率谱概率密度分布如图3所示,1~20Hz频带范围内的平均值约为-143.3dB(噪声水平的有效值为6.82×10-8m/s)。图4是震后1h内石场台的记录波形和时频能量分布结果。
同样,对石场台的时频包络特征曲线进行检测,共检测到39次触发结果。石场台记录中的S-P到时差约为16s,将自动检测到时与人工编目中Pg波震相到时差在15~17s范围内的事件视为同一事件,结果显示:正确触发的事件共有31次,正确率约83.8%,漏触发率约为16.2%。而采用STA/LTA自动算法共检测出触发事件45次,但其中正确的触发事件数仅有27次,正确率约为60.0%,漏触发率约为27.0%。通过以上结果可以看出,本研究提出的检测方法,在这2个指标上也明显优于STA/LTA算法的检测效率。为了对这2种算法的运算速度进行比较,将2组记录波形从0s处开始,以窗长为180s的间隔,渐进式增加记录数据长度进行计算,2种算法实际计算耗时对比如图5所示。对于处理3600s采样率为100Hz的数据,在数据记录长度小于2000s的阶段,时频包络特征算法的计算耗时与STA/LTA算法基本一致。随着数据长度的增加,时频包络算法的计算耗时的增加幅度逐渐略大于STA/LTA算法,这主要是由于随着记录数据长度的增加,计算时频能量分布所需耗时逐渐增加,但这种影响在实时处理过程中可以忽略不计,因为通常情况下实时检测的数据长度为s级或数十s,在这种情况下时频包络特征算法的计算耗时可以达到s级。
3 结论与讨论
本文针对密集余震序列的记录特征,研究了一种基于地震波波谱包络分布特征的快速触发检测方法。在继承声谱图像模式识别的正演逻辑触发模式的基础上,将其改进为以台站固有的地噪声水平为触发的判据。改进后的算法,将构建二维灰度图像转换为谱能量分布图,并且舍弃了原来需要构建不同信号之间的波形非线性图像和复杂识别模式的过程,在初至震相的触发效率上仅取决于台站记录频带内背景噪声固有的时频特征,这样不仅克服了由单一频率、无规则的瞬时大振幅而引起的误触发,还很好地避开了STA/LTA算法中设置触发阈值的问题。通过频谱分析精确分离出记录信号中与背景噪声有差异的信号后,继续沿用原方法中采用非线性标度缩放因子对大于台站背景噪声水平的能量进行归一化处理的方式,显著提高了记录信号中弱信号的信噪比,使得特征包络曲线的提取更加精确,因此在序列地震的触发检测中大大降低了主震尾波对后续地震检测的影响。
2组余震序列的实测结果表明:本文所提出的方法,相对STA/LTA算法自动检测结果,正确触发率提高约19.6%,漏触发率则降低了22.6%。这表明基于地震波波谱能量分布的检测方法具有更强的抗干扰能力。由于本文方法是通过提取包络特征曲线来进行初至震相的触发检测,因此具有与STA/LTA算法(即短时平均与长时平均值之比的曲线)相似的特点,即运行速度快,能够满足地震实时处理系统的技术要求。
初至震相的识别是建立在识别信号和噪声差异的基础之上,如振幅、频率、偏振、功率谱等。由于记录信号常常会受到很多干扰因素的影响,如震级大小、震中距、记录台站相对于震源的方位甚至记录系统故障等。因此,没有任何单一的方法可以保证初至震相的识别完全可靠;但从本文的实测结果来看,基于地震波波谱包络分布特征的检测方法,在密集余震序列的初至震相檢测中是具有明显优势的。
参考文献:
黄媛,吴建平,张天中.2008.汶川8.0级大地震及其余震序列重定位研究[J].中国科学:地球科学,38(10):1242-1240.
刘希强,周蕙兰,沈萍,等.2000.用于三分向记录震相识别的小波变换方法[J].地震学报,22(2):125-131
王俊,徐戈,孙业君.2009.江苏省区域地表背景噪声特性的分析[J].地震研究,32(2):155-161.
王俊,郑定昌,詹小艳,等.2013.基于背景噪声互相关格林函数的单台时间误差枯计[J].地震学报,35(6):888-901
王勤彩,陈章立,郑斯华.2009.汶川大地震余震序列震源机制的空间分段特征[J].科学通报,54(16):2348-2354
朱艾斓,徐锡伟,刁桂荃,等.2008.汶川MS8.0地震部分余震重新定位及地震构造初步分析[J].地震地质,30(3):759-767.
Allen R.1978.Automatic earthquake recognition and timing from singletrace[J].BSSA,68(5):1521-1532.
Bormadn P.2012.NewManual of Seismological Observatory Practice 2(NMSOP-2)Potsdam:Deutsches GeoForschungsZentrum GFZ,pp.1-65,doi:http://doi.org/10.2312/GFZ.NMSOP-2_ch8
Joswig M.1990.Pattern recognition for earthquake detection[J].BSSA,80(1):170-186.
Joswig M.1993.Single-trace detection and array-wide confidence asso-ciation of local earthquakes and explosions[J].Computers and Geo-sciences,19(2):207-221.
Leonard M,Kennett B L N.1999.Multi-component autoregressive tech-niques for the analysis of seismograms[J].Phys Earth Planet Interi,113(1-4):247-264.
Leonard M.2000.Comparison of manual and automatic onset time picking[J].BSSA,90(6):1384-1390.
Massa M,Ferretti G,Spallarossa D.2006.Improving automatic locationprocedure by waveform similarity analysis:An application in theSouth Western Alps(Italy)[J].Phys Earth Planet Interi,154(1):18-29.
McNamam D E,Boaz R I.2005.Seismic Noise Analysis System UsingPower Spectral Density Probability Density Functions:A Stand-A-lone Software Package[R].Virginia U S Geological Survey.Patane D,Ferrari F,Fernicci F.1999.First application of ASDP software:A case study at Mt.Etna volcano and in the Acri region(Southern It-aly)[J].Phys Earth Planet lnteri,113(1-4):75-88.
Sleeman R,Van E,Torild.1999.Robust automatic P-phase picking:Anon-line implementation in the analysis of broadband seismogram re-cordings[J].Phys Earth Planet Interi,113(1-4):265-275.
Stevenson P R.1976.Microearthquakes Flathead Lake,Montana:A studyusing automatic earthquake processing[J].BSSA,66(1):61-79.
Wang J,Teng T L.1995.Artificial neural network-based seismic detec-tor[J].BSSA,85(1):308-319.
Withers M,Aster R,Young C,Beiriger J,et at,1998.A comparison of se-lect trigger algorithMS for automated global seismic phase and eventdetection[J].BSSA,88(1):95-106.



摘要:以声谱图像模式识别为基本思想,改进了基于地震波波谱包络分布特征的初至震相检测方法。改进后的算法,首先将波形记录特征转换为谱能量分布,以台站固有背景噪声的时频特征为基准,提取出记录信号的时频包络特征作为事件触发检测的目标函数。为降低主震尾波对检测后续余震的影响,采用非线性标度缩放因子对大于台站背景噪声水平的能量进行归一化处理。通过2组密集余震序列的实测结果表明:相对STA/LTA算法自动检测结果,新方法正确触发率提高约19.6%,漏触发率则降低了22.6%,表现出更强的抗干扰能力和触发效率,且运行速度快,能够满足地震实时处理系统的技术要求。
关键词:余震序列;初至震相;地震波;波谱能量包络;峰值搜索
中图分类号:P315.3 文献标识码:A 文章编号:1000-0666(2018)02-0258-06
0 引言
完整、可靠的余震序列参数是中强地震发生后或密集震群序列活动时,确定主震发震构造、估计断层破裂尺度、序列后续趋势判定以及开展应急救援等工作关键的基础数据。研究表明,余震序列精定位是确定主震发震构造特征最为有效的途径之一(黄媛等,2008;朱艾斓等,2008):利用余震序列的震源机制解还可以进一步反演震源区构造应力场的分布特征(王勤彩等,2009)。然而,地震学家们通常需要滞后数天甚至更长的时间才能得到有关强余震序列较为完整、可靠的后续研究结果。其主要原因是目前地震实时处理系统所采用的STA/LTA算法对余震序列的检测效率较低,绝大部分余震需要震相分析人员通过查看连续记录波形进行查找。随着台站密度的日益提高,密集余震序列快速检测的数据量也将进一步增加。因此,研究一种快速、高效的地震事件触发检测算法,具有十分重要的现实意义。
自20世纪70年代以来,地震震相的触发检测一直都是国内外学者研究的重点领域,并取得了大量的成果。从最简单的以振幅大小作为触发标准到复杂的图像模式识别、自适应方法、神经网络法以及小波变换的主成分分析法等(Allen,1978;Joswig,1990;Wang,Teng,1995;Witherset al,1998;Patane et al,1999;Sleeman et al,1999;Leonard et al,1999,2000;刘希强等,2000;Massa et al,2006)。这些震相识别方法是根据信号与噪声之间的差异特征而提出,如振幅或能量、频率、波形的相似性、地震波传播方向和动力学特征(如偏振、频谱等),对于单个地震或特定的区域性地震而言,可取得较好效果。但这些复杂、有效的震相触发检测算法,通常由于运算速度较慢而难以满足实时处理的技术要求。
通常情况下,中、强地震发生后短时间内会在震源区附近发生大量的余震,绝大多数余震发震时间间隔极短,甚至相互重叠且处于主震的尾波中。例如,据国家地震台网中心统一编目结果,2008年汶川M8.0地震后50d内,四川地震台网以及应急流动台站共记录到余震总数超过1.6万次,余震最密集时1h内ML>1.0地震达179次;2014年新疆于田M7.3地震后5d内共记录余震总数3294次。尽管震相检测触发方面已有不少研究成果,然而针对地震序列快速监测的研究成果仍然较少。由于STA/LTA算法(短时平均与长时平均值之比)具有算法简单、速度快、便于实时处理等特点(Stevenson,1976),在地震事件的实时触发检测中,国、内外主要地震机构的处理系统仍普遍采用该算法。STA/LTA算法对于环境背景噪声水平低的台站来说非常有效,但它的抗干扰能力不够强,若记录中存在无规则、随机大振幅的干扰信号、或脉冲式噪声以及信噪比较差时,该算法的效率会大大降低。另一方面,在检测过程中,STA/LTA的触发阈值起了决定性的作用,阈值设置得高,小地震则不会触发;而当阈值设置得低时,则会出现大量的误触发。尽管在实际计算过程中有2种方案可供选择,即“锁定”LTA和连续更新LTA,但这2种方法仍有优缺点:“锁定”LTA值使记录系统一直处于触发状态,而连续更新LTA值时,会使尾波过早地被截断(Bor-mann,2006)。此外,采用STA/LTA算法检测余震序列中的初至时,主震尾波及余震之间的相互叠加就成为干扰STA/LTA算法的主要因素。
本文将针对密集余震序列的记录特征,以声谱图像模式识别方法为基本思想,实验一种基于地震波波谱包络分布特征为基础的初至震相快速检测方法,并将其应用于2次地震进行验证。
1 研究方法
Joswing(1990,1993)提出的声谱图像模式识别(Sonogram Pattern Recognition)方法,其基本思想是将各种类型的地震信号与临时噪声信号定义成不同的模式,在实时检测过程中,当与定义模式足够相似时,即被触发,该方法是一种正演的决定逻辑触发模式。触发模式或触发阈值的设置不依赖于地噪声水平,因为它在此阶段对地震信号和突发性噪声采用相同的处理方式。基本步骤为:(1)将记录波形进行非线性化的图像转换,即通过信号的谱能量构建二维灰度图像,其中黑度代表潜能量的密度,在处理过程中采用了非线性的标度缩放因子,使它与简单的谱密度图像有着很大的差异:(2)基于典型的地震信号和噪声建立不同的识别模式。如建立不同类型地震信號与交通、工业噪声、汽车、火车等大幅度噪声之间的模式等;(3)实时检测,即实现检测阈值和最相似模式的逻辑决定。其中(1)、(2)步中构建波形的非线性图像和识别模式难度较大且过程十分复杂,这也是该方法难以被广泛应用的原因所在。
本文是在上述基本思路的基础上,将其改进为波谱能量时频包络线识别模式,基本步骤为:
(1)沿记录波形连续滑动地计算一定窗长内信号的功率密度谱(PSD),在全频段内以1/8倍频为单位间隔计算平均功率谱,即计算在短拐角周期Ts和长拐角周期TL=2×Ts内的平均功率谱值,赋值给几何中心周期Tc[Tc=sqrt(Ts×TL)],记为矩阵Aij:
Aij=psd(fi,tj)(1)式中:fi代表第i个频率,tj代表j时刻的记录波形。
为了最大限度地突出地震信号的能量,同时避开噪声能量最强的频段(Peterson噪声模型中微震峰值频带1~10s),需要在计算前根据不同地震信号(P、S波)的卓越频带范围进行相应的滤波处理。
(2)记录信号的功率谱密度矩阵与该台稳定的噪声功率谱矩阵nij之比,记为Bij:
Bij=Aij/nij(2)式中:nij是根据每个台站背景噪声的功率谱概率密度函数计算得到。对于单个台站的记录,在某一频段内,将信号中高于该台背景噪声功率谱阈值矩阵的部分(即Bij中大于1处),通过非线性的标度缩放因子进行归一化处理,以降低大振幅信号对能量分布权重的影响,换言之,即提高弱信号(尤其是淹没在背景噪声中的信号)在能量分布中的比重。于是可根据高于台站背景噪声水平、归一化后的能量分布和持续时间,提取出地震记录波形在特定频带段内的谱能量时频包络曲线。
(3)通过设定谱能量的触发阈值对信号进行触发检测,这样触发检测就完全取决于台站随频率的噪声水平和各个频点上高于背景噪声水平的持续时间,在持续时间内的信号,即认为是有效的地震信号。
2 实测结果
2.1 江苏高邮M4.9地震余震序列
2012年7月20日20时11分,在江苏高邮与宝应交界处发生M4.9地震,这是近30年来江苏省陆地上发生的最大地震。距离主震震中最近的是宝应地震台,震中距约为36.8km。据江蘇省地震台网记录,震后4h内的宝应台共记录余震44次,其中震后1h内的余震为29次(表1)。为验证本文提出的方法,选取了震后1h内的连续记录波形进行回溯性实测。在提取波谱能量包络线之前,先确定被检测台站的各频点上背景噪声水平nij。本文中采用功率谱概率密度函数法计算nij(McNamara,Boaz,2005;王俊等,2009)。取宝应台背景噪声加速度功率谱概率密度函数80%的分布概率代表其背景噪声水平,如图1中黄色线条所示,在1~20Hz频带范围内的平均值约为-145.7dB(噪声水平的有效值约为5.16×10-8m/s)。
在震中距小于100km的地方震记录中,P波的周期约为0.05~0.2s,同时为避开背景噪声微震峰值的影响,在计算前对连续记录进行1Hz以上的Butterworth高通滤波处理。首先,将垂直向记录波形中高于各频点背景噪声水平的能量进行归一化处理,如图2b中红色区域所示,白色曲线即为根据时频能量分布提取出的特征包络曲线。对比实际记录波形(图2a)可以看出,在经过归一化后的能量包络曲线中,由于大振幅信号在能量分布中的权重被削弱了,除了可以清晰地展现出记录数据中震级较大(ML>3.0)的地震信号外,重叠在主震以及较大余震尾波中的微小余震信号也变得十分清晰,如在主震后600s时间窗内有多组清晰的峰值曲线。如图2c所示,当把台站背景噪声水平nij人为提高5dB时,可以看到记录信号中的大部分余震淹没在背景噪声中,导致无法分辨。这表明记录信号的时频能量特征分布主要取决于记录台站在频域内的背景噪声水平。事实上对于一个固定的地震台站而言,一般情况下背景噪声水平的源是相对稳定的(王俊等,2013)。因此,在准确求得台站的背景噪声水平后,采用以背景噪声水平基准的特征包络曲线来反映记录信号的特征是客观、可靠的。
随后,利用峰值搜索法对时频包络线进行触发检测,具体方法是:在设定的触发能量阈值Fc(图2b中黑色线条)线以上,根据峰值的持续时间(Tc)、坡度(Pc,即峰值的高度除以持续时间的1/2)阈值,进行峰值搜索①。图2b中黑色箭头表示在Fc=10Hz、Tc=20s、Pc=2时的触发情况,除主震外,还检测到29次触发事件。将触发结果与正式编目结果中宝应台的Pg波震相到时进行对比,以检验触发准确率,将触发时间误差在一定范围内的事件视为同一事件,本文中误差取值为2s。由于波谱能量时频包络线法检测到的位置是地震信号中能量分布最强的位置,对于地方震而言它对应的位置一般是S波的振幅最大位置处(图2b,c)。以人工地震编目中Pg震相到时为基准,宝应台实际记录的S-P到时差约为5s,因此将到时误差在4~6s范围内的事件视为同一事件。将准确触发事件数与触发总数之比,定义为准确率;未触发的事件数与实际事件数之比,定义为漏触发率。统计结果显示:采用波谱能量包络方法准确触发的事件共有26次,准确率约为83.4%,漏触发率约10.3%。相比而言,采用STA/LTA算法在触发阈值为3时的常规状态下,共检测出23次,但只有16次触发是有效的,准确触发率约为69.5,漏触发率达44.8%。详细的对应关系见表1。
2.2 新疆和静M6.6地震余震序列
为了进一步验证本文方法,选取1组更为复杂的序列进行实测。2012年6月30日5时7分,在新疆和静(43.4°N,84.8°E)发生M6.6地震,根据新疆地震台网记录结果,震后1h内共记录余震37次,距离震中最近的石场台(SCH台)震中距约为100km。石场台背景噪声的加速度功率谱概率密度分布如图3所示,1~20Hz频带范围内的平均值约为-143.3dB(噪声水平的有效值为6.82×10-8m/s)。图4是震后1h内石场台的记录波形和时频能量分布结果。
同样,对石场台的时频包络特征曲线进行检测,共检测到39次触发结果。石场台记录中的S-P到时差约为16s,将自动检测到时与人工编目中Pg波震相到时差在15~17s范围内的事件视为同一事件,结果显示:正确触发的事件共有31次,正确率约83.8%,漏触发率约为16.2%。而采用STA/LTA自动算法共检测出触发事件45次,但其中正确的触发事件数仅有27次,正确率约为60.0%,漏触发率约为27.0%。通过以上结果可以看出,本研究提出的检测方法,在这2个指标上也明显优于STA/LTA算法的检测效率。为了对这2种算法的运算速度进行比较,将2组记录波形从0s处开始,以窗长为180s的间隔,渐进式增加记录数据长度进行计算,2种算法实际计算耗时对比如图5所示。对于处理3600s采样率为100Hz的数据,在数据记录长度小于2000s的阶段,时频包络特征算法的计算耗时与STA/LTA算法基本一致。随着数据长度的增加,时频包络算法的计算耗时的增加幅度逐渐略大于STA/LTA算法,这主要是由于随着记录数据长度的增加,计算时频能量分布所需耗时逐渐增加,但这种影响在实时处理过程中可以忽略不计,因为通常情况下实时检测的数据长度为s级或数十s,在这种情况下时频包络特征算法的计算耗时可以达到s级。
3 结论与讨论
本文针对密集余震序列的记录特征,研究了一种基于地震波波谱包络分布特征的快速触发检测方法。在继承声谱图像模式识别的正演逻辑触发模式的基础上,将其改进为以台站固有的地噪声水平为触发的判据。改进后的算法,将构建二维灰度图像转换为谱能量分布图,并且舍弃了原来需要构建不同信号之间的波形非线性图像和复杂识别模式的过程,在初至震相的触发效率上仅取决于台站记录频带内背景噪声固有的时频特征,这样不仅克服了由单一频率、无规则的瞬时大振幅而引起的误触发,还很好地避开了STA/LTA算法中设置触发阈值的问题。通过频谱分析精确分离出记录信号中与背景噪声有差异的信号后,继续沿用原方法中采用非线性标度缩放因子对大于台站背景噪声水平的能量进行归一化处理的方式,显著提高了记录信号中弱信号的信噪比,使得特征包络曲线的提取更加精确,因此在序列地震的触发检测中大大降低了主震尾波对后续地震检测的影响。
2组余震序列的实测结果表明:本文所提出的方法,相对STA/LTA算法自动检测结果,正确触发率提高约19.6%,漏触发率则降低了22.6%。这表明基于地震波波谱能量分布的检测方法具有更强的抗干扰能力。由于本文方法是通过提取包络特征曲线来进行初至震相的触发检测,因此具有与STA/LTA算法(即短时平均与长时平均值之比的曲线)相似的特点,即运行速度快,能够满足地震实时处理系统的技术要求。
初至震相的识别是建立在识别信号和噪声差异的基础之上,如振幅、频率、偏振、功率谱等。由于记录信号常常会受到很多干扰因素的影响,如震级大小、震中距、记录台站相对于震源的方位甚至记录系统故障等。因此,没有任何单一的方法可以保证初至震相的识别完全可靠;但从本文的实测结果来看,基于地震波波谱包络分布特征的检测方法,在密集余震序列的初至震相檢测中是具有明显优势的。
参考文献:
黄媛,吴建平,张天中.2008.汶川8.0级大地震及其余震序列重定位研究[J].中国科学:地球科学,38(10):1242-1240.
刘希强,周蕙兰,沈萍,等.2000.用于三分向记录震相识别的小波变换方法[J].地震学报,22(2):125-131
王俊,徐戈,孙业君.2009.江苏省区域地表背景噪声特性的分析[J].地震研究,32(2):155-161.
王俊,郑定昌,詹小艳,等.2013.基于背景噪声互相关格林函数的单台时间误差枯计[J].地震学报,35(6):888-901
王勤彩,陈章立,郑斯华.2009.汶川大地震余震序列震源机制的空间分段特征[J].科学通报,54(16):2348-2354
朱艾斓,徐锡伟,刁桂荃,等.2008.汶川MS8.0地震部分余震重新定位及地震构造初步分析[J].地震地质,30(3):759-767.
Allen R.1978.Automatic earthquake recognition and timing from singletrace[J].BSSA,68(5):1521-1532.
Bormadn P.2012.NewManual of Seismological Observatory Practice 2(NMSOP-2)Potsdam:Deutsches GeoForschungsZentrum GFZ,pp.1-65,doi:http://doi.org/10.2312/GFZ.NMSOP-2_ch8
Joswig M.1990.Pattern recognition for earthquake detection[J].BSSA,80(1):170-186.
Joswig M.1993.Single-trace detection and array-wide confidence asso-ciation of local earthquakes and explosions[J].Computers and Geo-sciences,19(2):207-221.
Leonard M,Kennett B L N.1999.Multi-component autoregressive tech-niques for the analysis of seismograms[J].Phys Earth Planet Interi,113(1-4):247-264.
Leonard M.2000.Comparison of manual and automatic onset time picking[J].BSSA,90(6):1384-1390.
Massa M,Ferretti G,Spallarossa D.2006.Improving automatic locationprocedure by waveform similarity analysis:An application in theSouth Western Alps(Italy)[J].Phys Earth Planet Interi,154(1):18-29.
McNamam D E,Boaz R I.2005.Seismic Noise Analysis System UsingPower Spectral Density Probability Density Functions:A Stand-A-lone Software Package[R].Virginia U S Geological Survey.Patane D,Ferrari F,Fernicci F.1999.First application of ASDP software:A case study at Mt.Etna volcano and in the Acri region(Southern It-aly)[J].Phys Earth Planet lnteri,113(1-4):75-88.
Sleeman R,Van E,Torild.1999.Robust automatic P-phase picking:Anon-line implementation in the analysis of broadband seismogram re-cordings[J].Phys Earth Planet Interi,113(1-4):265-275.
Stevenson P R.1976.Microearthquakes Flathead Lake,Montana:A studyusing automatic earthquake processing[J].BSSA,66(1):61-79.
Wang J,Teng T L.1995.Artificial neural network-based seismic detec-tor[J].BSSA,85(1):308-319.
Withers M,Aster R,Young C,Beiriger J,et at,1998.A comparison of se-lect trigger algorithMS for automated global seismic phase and eventdetection[J].BSSA,88(1):95-106.

