网站首页  词典首页

标题	一元线性回归分析方法与工人需求量的预测
范文	张少坚 摘要：“用工荒”在一些地区时有发生。一个企业到底需要多少工人，估算方法各不相同。估算准确，既可以节省人力资源成本，又能实现预期的生产目标。本文运用统计学中的一元线性回归分析方法预测工人需求量，通过实证解析，揭示出以工时为自变量预测工人需求量的一元线性回归分析方法的应用要点，并最终提出应用建议。 关键词：一元线性回归分析方法 用工需求 年平均 人数 工时 中图分类号：F243 文献标识码：B Application of unitary linear recursive analysis means in worker needed- quantity forecast ZHANG Shao-jian （AVIC XAC，Xian 710089 ，China） Abstract： Labor Shortage appear sometime in some prefecture. Estimating means vary， of workers an employer demand after all. Accurate is the estimating ， an employer is able not only to reduce human resources costs， but also to successfully achieve production plan aim .By analysis， which applying unitary linear recursive analysis means in statistics， of the living examples ，and practical evaluation of recurrence value， deviation， fully unfolding the application key points of unitary linear recursive analysis means of workers needed- quantity forecast by manhour independent variable， the article advance the application advice . Key words： Unitary Linear R ecursive Analysis Means；Annual Average Number Of Workers；Man- hour 我需要多少工人？这是制造业企业主都遇见过的问题。解决这个问题通常的做法是根据往年产量与工人数匹配的比例，计算与未来产量相匹配的工人数。即：工人数y=比例系数a×产量x，这种计算方法简单易行，適用于产量与工人数成正比例函数关系的情况，这种情况多为劳动密集型企业。对于劳动密集型向资本和技术密集型逐年转化的企业，其产量与工人数不一定成正比例函数关系，而呈现的是相关关系。如船舶和航空航天制造等资本和技术含量较高的高科技企业。在产量与工人数具有相关关系的情况下，统计学中线性回归分析方法为工人需求量的预测提供了一个很好的预测方法。 一、一元线性回归分析方法自变量的选择 第一、当产品属同品种同规格时，产品具有可比性，产量可直接作为自变量。而当产品品种规格不相同时，产品没有可比性，需选择与产量对应的工时作为自变量。第二，因管理需要而将工时分类为商品工时（销售产值的衡量指标）和总工时（工人实际劳动量的衡量指标），应选择与生产工人人数相关性较强的那类工时作为自变量，即相关系数较大的那类工时作为自变量，以保证回归方程有较强的线性显著性水平，从而使回归预测值更接近观测值。 二、一元线性回归分析方法在Excel中的实现 例：2016年年初，秦航公司根据2016年计划产量预测工人年平均人数（12个月平均每月工人人数）。统计人员收集、整理出1991～2015年期间该公司的产品产量、工时及工人年平均人数的数据资料，见表1。已知，2015年年全部职工实际年平均人数为237人，2011～2015年5年平均全员劳动生产率实际为5094小时/人，2016年该公司计划生产不同品种不同规格的产品11件。 2016年年初，统计人员根据计划产量预估2016年产品商品工时和总工时分别为1300000小时和1280000小时。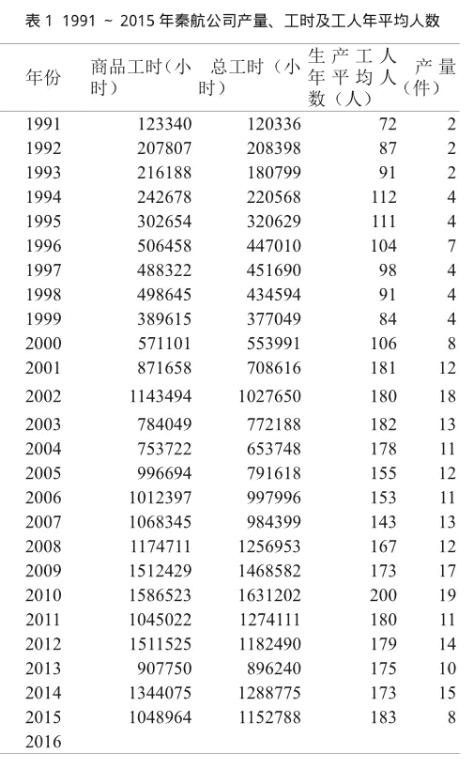 该公司2016年全年实际产品产量为10件，实际完成商品工时和总工时分别为1204057小时和1123723小时，实际工人年平均人数为177人。1991～2015年秦航公司产量、工时及工人年平均人数见表1。 （一）建立一元线性回归方程 秦航公司产品品种规格不同，不能直接以产量作为自变量，应以商品工时或总工时为自变量进行回归分析。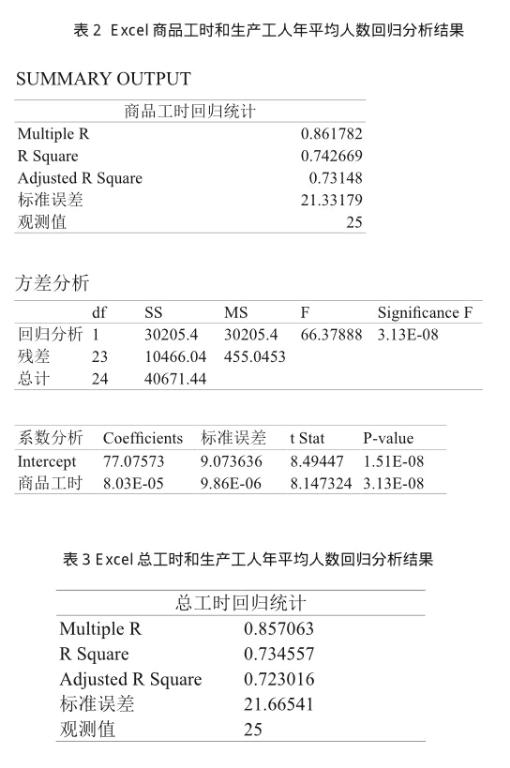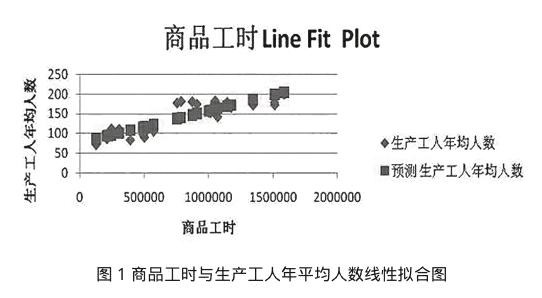 在Excel表中，选择数据分析选项中的〔回归〕分析工具，回归分析输出结果见表2；商品工时与生产工人年平均人数线性拟合如图1；总工时和生产工人年平均人数回归分析结果如表3。 因为表2中的商品工时回归统计的相关系数0.861大于表3中的总工时回归统计的相关系数0.857。所以，本案应选择商品工时作为自变量建立一元线性回归方程。根据商品工时系数分析表，得回归方程为：Y=77.08+0.00008X（2.1式）。 （二）回归方程的评价与检验 2.1式经济含义：其它影响因素不变，商品工时每增加100000小时，工人平均增加8人。 商品工时回归统计表中，商品工时与工人人数相关系数R=0.861，中度相关。判定系数R2=0.74，表示商品工时可以解释工人年平均人数74%的变动 。 方差分析表中，回归方程显著性F检验伴随概率sig值=0.00<0.05（事先给定的显著性水平α=0.05）[1]，2.1式的线性关系存在。 系数分析表中，回归系数显著性t检验伴随概率P-value=0.00<0.05（事先给定的显著性水平α=0.05），解释变量X对因变量Y的线性效果显著。 评价与检验的结果表明2.1式能应用于分析与预测[2]。 预测2016年工人年平均人数： Y=77.08+0.00008×1300000=181（人）。 三、回归值的实用性评价 （一）直观评价 评价目的：通过经验比较，工人年平均人数（12个月平均每月工人人数）的区间估计。在表1中观察比较可知，2016年预估的商品工时1300000小时和总工时1280000小时分别与2014年的商品工时1344075小时和总工时1288775小时最相近。2.1式的计算的结果181人，与2014年工人年平均人数173人相差8人，估计2016年工人年平均人数在173～181人之间，即：177±4（人）。案例中实际工人年平均人数为177人，正好落在该区间内。由此可见，工人年平均人数173～181人的区间估计可靠性较强，直观评价效果显著。 （二）全员劳动生产率评价 评价目的：预测全员劳动生产率水平（一般应大于或等于近几年平均全员劳动生产率）。预测2016年全员劳动生产率之前，首先要计算出2016年全部职工年平均人数。2016年全部职工年平均人数=2015年全部职工实际年平均人数237+（回归预测值181人-2015年工人年平均人数183）=235人。2016年全员劳动生产率的预测值=1280000/235=5447（小时/人），大于该厂5年平均全员劳动生产率5094，2016年全员劳动生产率的预测值令人满意。 四、误差分析 （一）随机误差 随机抽样误差是由调查样本随机因素引起的不可避免的误差，受样本数、样本方差、概率度（显著性水平）的影响。实例分析中存在一些不足之处。受客观条件限制，采集的样本数有限，影响误差大小的样本数n=25<30，样本容量较小[3]，不利于减小随机性抽样误差，从而影响预测精确度。 （二）非随机误差 非随机抽样误差是除随机抽样误差以外的所有误差，存在于调查分析的全过程。主要来源于调查数据的缺失和错误、整理分析过程出现的差错和误判。回归值181人比2016年实际工人年平均人数177人相差4人。2016年年初预估的商品工时1300000小时比2016年底实际完成商品工时1204057小时高95943小时。若年初预估的商品工时为1200000小时更接近实际完成值1204057小时，则2.1式预测的人数为174人，比实际人数177人仅相差3人，人数回归值与实际值误差进一步缩小。从此可以看出，自变量的预估值是影响因变量预测误差的重要因素，自变量预估值越接近观测的实际值，因变量回归值与观测值之间的误差越小。 五、一元线性回归分析方法的应用建议 （一）尽量增大样本容量 样本数据是生产运营的结果，我们无法调整改变。但是，在条件允许的情况下，我们应尽量增大影响预测误差的样本容量（n≥30），以控制减少回归分析产生的随机性误差。 （二）选择切合实际的自变量预估值 回归方程中的自变量往往是经验预估值，易受人为主观因素影响。无论是选择商品工时做自变量或是选择总工时做自变量，选择切合实际的自变量预估值，对于控制减小因误判给回归分析预测带来的非随机性误差、保证因变量的回归值更接近实际水平非常重要。 （三）进行必要的实用性评价 建立和使用回归分析的数学模型，需要某些假设条件，而生产运营不可能完全按照模型规定的假設条件去运行。假设检验以推断统计理论为依据，建立在概率基础上的推断，推断结果有一定的可信度或风险。因此，用回归分析法预测工人需求量，需对回归预测值进行实用性评价，包括直观评价和劳动生产率评价，据此预测工人需求量的变化区间和劳动生产率水平（一般应大于或等于近几年平均劳动生产率），做到未雨绸缪，心中有数。 参考文献： [1] 施雨，李耀武.概率论与数理统计应用[M].西安：西安交通大学出版社，1998：140. [2] 全国统计专业技术资格考试用书编写委员会.统计业务知识[M].北京：中国统计出版社，2013：301. [3] 刘飞.高级统计师实务教程[M].西安：陕西人民出版社，2012：27.
随便看	高校图书馆建设海南自由贸易港数据库研究 公共管理视角下激励机制领域的问题 大数据精准扶贫服务平台助力乡村脱贫与致富研究 基于城市系统论的政策性金融机构作用机制研究 国有企业员工流失的原因和对策分析 新冠疫情对我国白色家电企业盈利能力的影响 生态理念在园林景观设计中的运用 兰州市中小企业自主创新激励机制研究 “互联网+”背景下企业内部审计发展探索 保障性住房项目财务风险控制研究 论工业园区的金融服务体系构建 论会计事务所审计风险控制与防范措施 业财融合背景下的信息系统审计研究 基于审计结果谈企业财经管理工作的重要性 构建气象部门审计信息化系统的思路及效果初探 新税法背景下的企业会计税务筹划措施分析 简述经济新常态下企业会计发展方向及创新转型 试论经济新常态背景下企业财务会计集中核算的问题及解决措施 小企业财税政策现状及对策 基于财务共享服务下的“互联网+”时代管理会计信息化 探析税制改革对企业财务与会计的影响和对策 跨境电子商务物流模式创新与发展趋势研究 肃北县乡村振兴战略实施情况的调查与思考 产业融合发展、农产品供需结构与农业供给侧改革核心探寻 集成管理理论在建设项目全过程造价咨询业务中的应用研究 non-purchase nonpurchaser nonpurchasers nonpurchases nonpurification nonpurifications nonpurifying nonpurposive non-quaker non-quakerish non-quakers nonqualification nonqualifications nonqualifying nonqualitative nonqualitatively nonqualities non-quality nonquality nonquantifiable nonquantitative non-quantitative nonquantitatively nonquantitativeness nonquantitativenesses 谚语是日常经验的女儿 谚语词典 谛 谛信 谛分审布 谛号 谛听 谛味 谛妄 谛定 谛实 谛审 谛思 谛料 谛晓 谛眂 谛绎 谛观 谛视 谛认 谛语 谛读 谛辨 谜 谜作

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。