《基于无人机的航拍影像快速拼接技术研究》-管理学论文，管理论文-论文范文参考-科学狗论文网

标题

基于无人机的航拍影像快速拼接技术研究

范文

金剑武海彬刘文华

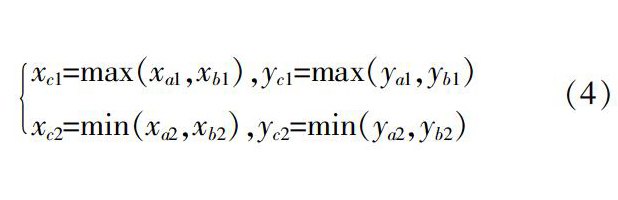
[摘? ? 要] 本文采用基于顾及重叠的面Voronoi图构建影像拼接网络，生成目标区域全部影像所对应的Voronoi多边形，依照影像顺序依次进行镶嵌处理，形成初步拼接成果图。应用基于Wallis滤波器的多片色彩均衡算法，进行影像匀光操作，实现拼接影像间的自然过渡。本文采用C++编程语言实现无人机影像特征提取、粗差消除、光束法平差、影像色彩一致性处理等环节，设计并开发出界面友好型无人机航拍影像自动拼接软件系统，能够快速进行影像拼接处理，获取良好的拼接效果。

[关键词] 无人机影像拼接;拼接线;色彩均衡

doi ： 10 . 3969 / j . issn . 1673 - 0194 . 2018. 21. 071

[中图分类号] F270.7;TP391.41? ? [文献标识码]? A? ? ? [文章编号]? 1673 - 0194（2018）21- 0166- 05

1? ? ? 无人机影像镶嵌算法

影像镶嵌（image mosaic）是指对具有重叠区域的多幅影像按照一定规则进行坐标变换，将全部影像规范到统一的坐标框架下，初步拼接成一幅覆盖整个目标区域的大型影像的过程[1]。影像拼接线的自动生成是镶嵌任务中的关键环节，现有的拼接线生成方法多只关注于相邻的两幅影像间单条拼接线生成情况，这类方法在整个拼接区域能构建多条拼接线，各拼接线具有独立性，只能按照影像顺序依次拼接，不利于直接生成最终镶嵌成果图。由于拍摄环境的影响，航空影像内部及影像之间在亮度分布上存在不同程度的差异，对其进行色彩均衡处理可以提升影像清晰度，获取更佳拼接效果，影像匀光操作十分重要。本文介绍无人机影像拼接优化策略，采用基于顾及重叠的面Voronoi图的拼接线网络自动生成算法和基于Wallis滤波器的多片色彩均衡算法，实现无人机影像快速镶嵌与色彩一致性处理操作。

2? ? ? 无人机影像拼接线自动生成

2.1? ?顾及重叠的面Voronoi图

Voronoi图[2]是计算几何中描述对象空间邻近关系的基础数据结构，一般用于求解点集、面元、空间几何体等几何对象的距离相关问题。面Voronoi图[3]是以面元为空间目标，基本运算单元是两个或数个互相分离的独立平面的集合，如图1所示。无人机获取的相邻航拍影像相互重叠，影像面元不具备独立性，因此无法应用面Voronoi图构建影像间拼接线，潘俊等人基于此提出了顧及重叠的面Voronoi图能够很好地解决问题。

在待拼接的影像为有限区域的情况下，可使用顾及重叠的面Voronoi图构建拼接线。无人机所获取的任意两幅相邻影像都具有60%-80%的重叠区域，所对应的非重叠区域对面Voronoi图的生成具有一定约束，在此约束下重新划分相邻两幅影像的重叠区域，并分别保留多边形所分割两幅影像间的对应区域，将其归于非重叠部分，生成新的拼接影像。

2.2? ?影像拼接线自动生成

在获取影像时，每张影像相互独立且依照中心投影成像，影像的中心部位投影质量较好，而用以进行镶嵌的影像边缘部分则会产生一些灰度差异，基于顾及重叠的面Voronoi图所选取的初始拼接线能使接边区域尽可能靠近相邻两幅影像的中心区域，均衡地剔除两边影像的失真边缘，确保最佳拼接效果。考虑到顾及重叠的面Voronoi图在重叠区域能划分产生无间隙、高吻合拼接线，对原始平面进行剪裁后再无重叠区域，高效剔除冗余数据，所划分出的区域保持结果唯一性，不存在多变情况，符合影像镶嵌的需求，故将其应用于大范围无人机航拍影像拼接线的自动生成中。此方法能够对各相邻影像重叠区域进行有效划分，形成每幅无人机影像的有效镶嵌多边形，计算影像对应的有效拼接范围，高效且快速地构建拼接线。该方法的结果与影像坐标相关，但不受影像顺序影响，可以提高拼接处理的灵活性，满足无人机影像快速镶嵌的需求。

相邻影像共用一段或数段Voronoi多边形公共边，全部影像生成的面Voronoi彼此相连，全部接边线构成目标区域的拼接线网络，顾及重叠的面Voronoi图的生成是构建拼接线的关键所在。首先确定相邻影像间重叠区域的范围，定义一个新的面集来表示原始无人机影像;接着，考虑重叠区域的大小，生成顾及重叠的面Voronoi图，求得全部影像所对应的Voronoi多边形;解算相邻影像的拼接线，即各Voronoi多边形间的公共边，拼接线彼此互相连接就构成所需要的拼接线网络。

2.3? ?确定影像重叠范围

在构建影像拼接线网络之前，需要确定相邻影像的重叠区域，在重叠区域中生成影像拼接线，这样既能剔除冗杂无用数据，更降低了计算机程序运算量。航带中的无人机影像是沿飞行方向快速、依次拍摄的，可以忽略影像间大小差异，无人机影像经过坐标投影变换后所得到的影像按照矩阵形式存储，如图2所示，用灰度值为0的像素填充影像周边无信息区域，纠正后影像排列规则，相邻影像的重叠情况也较为简单。对两幅图像（也就是两个矩形）的相交情况进行正确判断是生成有效拼接线的重要前提。本文假定影像的重叠情况有以下3种，如图3所示。

假设给定的两个影像为A和B，影像A所在存储矩阵的左上角坐标为（xa1，ya1），右下角坐标为（xa2，ya2），影像B所在存储矩阵的左上角坐标为（xb1，yb1），右下角坐标为（xb2，yb2）。判断两个矩形是否相交，只要确定两个矩形的中心坐标的水平和垂直距离，只要这两个值满足某种条件就可以相交。计算影像A和B的宽、高分别记为Wa，Ha，Wb，Hb：

可以求出影像A和B的中心坐标（xa3，ya3）、（xb3，yb3）：

当同时满足公式时，两幅影像则相交。

设相交的重叠区域为C，记C的左上角坐标为（xc1，yc1），右下角坐标为（xc2，yc2），则有：

2.4? ?顾及重叠的面Voronoi多边形的生成

由2.3节可知每个顾及重叠的面Voronoi图的生成都包含两个步骤：①确定相邻影像间重叠区域，在该区域生成影像中轴线;②计算各影像对应的Voronoi多边形。

2.4.1? ?计算重叠影像间中轴线

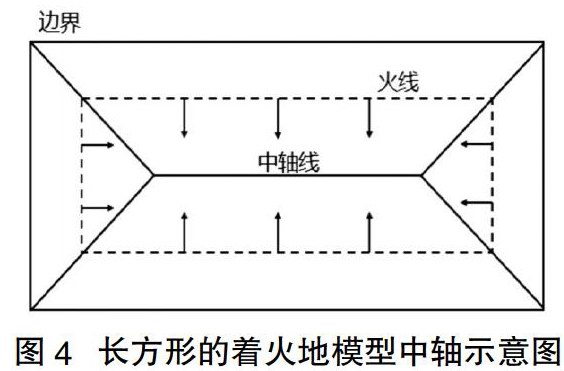
图像的中轴最开始被Blum形象地定义为着火地模型（Grass-fire model），[4]如图4所示。对于平面几何图形而言，其任意两条边界都存在一个内切圆，这些内切最大圆圆心的轨迹构成多边形中轴线，且中轴线上的点到多边形的对应边界的距离相等。

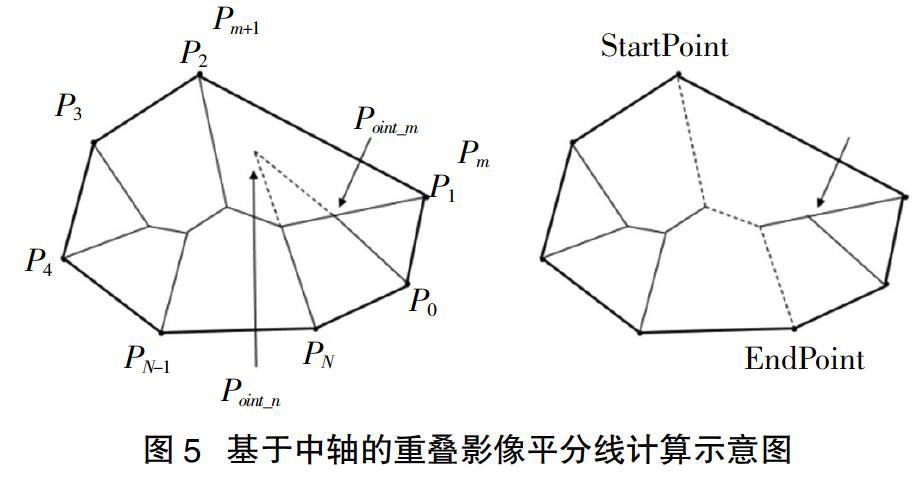
在上一步中确定了相邻影像间重叠区域，又根据中轴定义可知，我们所需求解的重叠区域平分线即是图像中轴的一部分，周培德[5]等人提出的简单多边形、凸多边形中轴算法，本文以该算法思想为依据，实现重叠区域中轴提取算法，具体步骤描述如下：

假设多边形有N个顶点，沿逆时针方向分别命名为P1，P2，…，PN，并且Pi-1和Pi+1都是Pi的相邻顶点。

（1）依次计算顶点Pi（i=1，2，…，N）的角平分线。

（2）任意相邻顶点Pi和pi+1角平分线的交点设为qi，依次计算交点qi到多边形对应边PiPi+1的距离di。

（3）设参数d=min（d1，d2，…，dN），以d=d1的情况为例进行说明，按逆时针方向重新排列顶点顺序，使得d1对应的顶点q1到对应边的距离最小。当di有多个最小值时，可任意选择其中的某di做如上处理。

（4）以重新排列后的顶点P0为起始点，即令StartPoint=P0，m=1，n=N，求解顶点Pi与顶点Pm、Pi与Pn的角平分线交点point_m、point_n。

（5）计算点间欧式距离，若d（point_m，StarPoint）

（6）若d（point_m，StarPoint）>d（point_n，StarPoint），则改变起始点为StarPoint=point_n，n--。

（7）保存上一步中生成的中轴转折点，编号为J1，J2，…，JN，并记录每个中轴转折点对应的多边形顶点;线段PmPm+1，PnPn-1延长线相交，计算该夹角的平分线teml，teml与顶点Pm+1，Pn角平分线相较于point_m和point_n。

（8）重复执行步骤（5），当m=n时停止运算。

（9）按照顺序依次连接全部StarPoint及多边形顶点，构建多边形中轴线。

如图5所示，图中虚线即所求多边形的中轴线。

2.4.2? ?生成影像Voronoi多边形

根据以上介绍的原理方法，获取任意兩个相邻影像重叠区域的中轴线，即重叠面平分线之后，还需用此平分线对相应无人机影像进行划分与剪裁操作，去除变形较大的边缘部分，生成影像所属的Voronoi多边形，以便生成全部影像的Voronoi图，具体实现过程如下：

（1）按照无人机影像航带间序列号以及航带号依次确定相邻影像间重叠区域范围。

（2）依据航带内影像排列顺序依次计算相邻影像的重叠区域平分线，再计算航带间相邻影像重叠区域平分线。

（3）对于一对部分区域重合的无人机影像，用生成的平分线剪裁影像重叠部分的外部区域，并保存结果。

（4）对于位于航带中间的影像，其每次剪裁结果都作为下次处理的初始输入，再完成多次划分后可生成当前无人机影像的初始Voronoi图。

（5）再按照上述操作，对航带间影像重叠区域做局部剪裁，计算每幅影像所属Voronoi多边形，每幅正射影像都被切割成互不重叠的不规则多边形，这样就完成了整个区域影像Voronoi图生成操作。

在生成无人机影像Voronoi图的过程中，依据Weiler[6]，刘勇奎[7]所提出的多边形剪裁算法来确定重叠区域中平分线的出点与入点。其具体思路可简述为：以相邻两幅无人机影像的重叠区域为参考，确定区域平分线的入点和出点，入点和出点一一对应，一对出入点确定一条平分线，当遇到出点时完成一次划线过程;算法跳转至相同重叠区域继续追踪以求解新的区域平分线，不进行重复操作直到回至起始入点，此时求解出整个重叠区域全部的区域平分线。

2.5? ?生成拼接线网格

从上一步中获取了无人机航拍区域中全部影像Voronoi多边形，可以看出两幅相邻影像重叠区域具有形状相同的公共边，计算并保存该公共边信息，即生成一条拼接线，按照一定规则连接众多拼接线的顶点，便可构建整个航拍区域的拼接线网络。考虑到无人机影像具有较大的航向重叠度，在这种高重叠的情况下，不能生成正确的拼接线网络，第一幅图像与第三幅图像之间也有重叠，这样两两生成的拼接线会相互交叉，出现拼接漏洞的情况。解决这一缺陷的方式之一是对图像进行抽片，即隔片进行拼接，但在飞机飞行姿态不稳定的时候有可能会出现拍摄漏洞，需要对这类情况谨慎处理。将全部影像依据拼接线网络进行投影后，对其进行多分辨率融合，可解决曝光差异问题以及弱化拼接线痕迹。

3? ? ? 基于Wallis滤波器的多片色彩均衡算法

影像色彩均衡[8]算法又称影像匀光算法，基于Wallis滤波器的匀光算法是影像间自动化的匀光处理，也是目前使用较多的一种方法。Wallis滤波器具有一定的特殊性，它通过局部影像变换以增强原始影像间灰度、色彩反差，适用于多幅影像间色彩、亮度差异调整。

3.1? ?Wallis滤波器

Wallis滤波器具有一定的特殊性，通过进行影像的局部区域变换，将影像局部区域的灰度均值及方差映射到给定的对应值，并且使不同区域影像的灰度方差和灰度均值都近似相等，以模糊影像区域间较大反差，增强影像中灰度微小信息，这种特殊的滤波器广泛应用于影像配准、融合等图像处理任务中。

Wallis滤波器的一般表达式为：

可见，当r1>1时，可以看作高通滤波，当r1<1时，则可视为低通滤波。经典的Wallis滤波器中b和c同时取1，此时该滤波器的表达形式为：

当mg=mf，sg=sf，时，使用Wallis滤波器对原始图像进行处理不会引起影像灰度的变化。

3.2? ?基于Wallis滤波器的影像匀光

一幅影像的均值反映其色调与亮度，而标准偏差则反映影像的灰度动态变化范围。在无人机上搭载普通相机进行对地拍摄，所获取的影像一般能满足70%的航向重叠以及50%的旁向重叠，相邻影像重叠区域间地物具备一定相关性，在理想飞行情况下相邻的若干幅影像应具有近似一致的色调、亮度和反差，因而也具有近似的灰度均值与标准偏差。无人机影像中真实场景的色彩信息在色彩空间上具有连续性，而且影像局部色彩差异对影像整体色彩信息的影响较小，可以确保相邻影像间的灰度均值、标准偏差近似一致性，因此Wallis滤波器可以用于进行测区多幅重叠影像的色彩一致性处理。而且基于Wallis滤波的影像匀光方法简单、快速、有效，当不同影像范围内地物信息变化不大时，就能取得很好的效果，十分有利于大尺寸无人机影像的快速拼接。

基于Wallis滤波器的多幅无人机影像匀光处理的基本步骤为：

（1）统计航测区域内相邻影像的灰度均值和标准偏差，根据统计数据确定输出图像的目标均值和标准偏差，即分别选取各影像灰度均值的平均值、方差最大值为目标均值、目标标准偏差。

（2）以此目标值为基准，将选取的目标均值和方差带入Wallis滤波器表达式中，计算乘性系数和加性系数，然后对侧区内所有影像进行色彩均衡处理。

基于Wallis滤波的多片影像匀光是对影像进行线性变换，其中乘性常数决定影像灰度级间的距离，加性常数决定影像灰度偏移量，使加性常数取0以上数值、乘性常数取1或1以上数值可避免灰度流失、灰度合并现象，能够很好地保存原始影像的地物纹理、细节信息。Wallis匀光算法能够对不均匀无人机航拍影像的暗部区域进行灰度增强，同时对亮度区域进行灰度压缩，经过Wallis匀光处理后的影像在影像色调和细节信息上都能与原影像保持一致。

4? ? ? 实验与分析

4.1? ?Voronoi图拼接线生成

当前计算机硬件资源是有限的，为了实现大量、海量影像的拼接，不能简单地将所有影像拼接的操作都放在计算机内存中进行。本文在匹配完成后，求取各影像相对于参考影像的透视变换矩阵，并通过L-M[9]算法平差对各影像的透视变换矩阵进行整体调整以消除误差积累，然后对所有的影像做透视变换并保存，最后对透视变换后的影像进行镶嵌，镶嵌线基于顾及重叠的面Voronoi图生成。

为了对基于顾及重叠的面Voronoi图的拼接线的生成效果进行说明，本文先对9幅单航带影像进行拼接线提取测试。图6（a）是经过透视变换得到的影像，图6（b）是每一幅图像对应的Voronoi图拼接线的图像化表示，本文用黑白二值图像进行表示：白色区域表示对应影像的有效部分，黑色部分表示对应影像需要裁切掉的部分。由于航飞时飞机姿态不稳定，导致影像间的航偏角（Kappa角）较大，所以投影后的影像相比于原始影像变形较大，生成的Voronoi拼接线也不规则。另外需要注意的是，Voronoi圖并不能保证每幅影像对应的拼接线是单个多边形，有可能一幅图像对应的拼接线由多个多边形（multi-polygon）组成，如图7所示。

为了对整个算法进行测试，本文选用一个测区的完整数据进行拼接测试，该测区有220幅影像，由SONY ILCE-7R相机拍摄，单幅影像的分辨率为7 360×4 912（约3 615万像素），整个测区较为平坦，如图8所示。

由图8结果可以看出，对于较为平坦的地区，通过二维透视投影变换完全满足无人机影像拼接的需求，通过匹配的粗差剔除以及L-M算法消除误差累积的策略处理以后，影像之间几乎没有什么错位，整个影像拼接效果良好。

4.2? ?Wallis匀光匀色

相比于卫星影像和有人机拍摄的航空影像，无人机一般搭载普通数码相机，飞机姿态也不稳定，拍摄时更容易受到拍摄角度、曝光等因素的影响，获取的影像常常会存在着较大的色彩和亮度差异，对于这一类影像，有必要进行影像的匀光匀色处理，本文主要利用Wallis滤波器进行无人机影像的匀色处理。

为了对Wallis匀光匀色的效果进行测试，本文选用了一组部分影像被云遮挡的数据进行实验，如图9 （a）中的第二幅影像和第三幅影像，由于被云遮挡后影像色调明显偏暗，和第一幅影像具有较大的色彩差距。图9 （a）是Wallis匀光匀色前的影像，图9 （b）是经过Wallis匀光匀色处理之后的影像，实验中以第一幅影像的均值和方差作为参考值，对另外的影像进行均值和方差的调整，由图中结果可以看出，经过Wallis匀色以后，原來影像之间较大的色彩差异能够有效得到调整，匀色以后影像之间的亮度和色彩趋于一致。

为了对Wallis匀光匀色的效果进一步进行说明，本文对整个测区的影像进行了拼接测试，如图10和图11所示。由于拍摄时天气较阴，测区的绝大部分影像偏暗，同时因为一些遮挡和反射的因素，有的影像内部色彩和亮度不一致。

图10是经过Wallis匀光匀色处理之后拼接而成的效果图。首先从整体效果来看，没有经过Wallis匀光处理的影像拼接图明显偏暗，影像存在着亮度和色彩的不一致，而经过匀光匀色处理之后，拼接后的影像亮度和色彩基本一致，整个影像的目视效果更好;从影像局部来看，没有经过匀光匀色处理的拼接图会出现“斑块状”图斑，这在经过匀光处理以后的影像拼接图上是没有的。

由于方差在一定程度上反映了影像的细节和偏差，因而最大的方差能够最大化地保证影像的细节，所以本文的标准方差取所有影像方差的最大值;而由于影像的亮度值在一定程度上取决于影像质量的好坏，当亮度差异特别大或者亮度过高/过低时，建议人工选取，一般默认设为影像的平均灰度均值。

5? ? ? 结? ? 语

本文分别从拼接线构网、影像色彩均衡处理角度介绍了两种影像拼接效果优化策略：首先是采用基于顾及重叠的面Voronoi图构建目标区域整体拼接线网络，先确定每对相邻影像的重叠范围，再提取重叠区域中轴线，生成顾及重叠的面Voronoi多边形，依序对测区影像进行剪裁，得到每幅影像对应的Voronoi多边形，多边形接边相连便形成整个目标区域的拼接网络，实现无人机影像的良好拼接;针对无人机影像色彩不均衡现象，采用Wallis滤波器进行影像匀光操作，通过统计影像灰度均值与方差，利用Wallis滤波器调整影像灰度的线性分布，保持多幅影像间色调、亮度的一致性，可以较好地对无人机航拍影像实现匀光处理。

主要参考文献

[1]Zeng L，Zhang S， Zhang J，et al. Dynamic Image Mosaic via SIFT and Dynamic Programming[J]. Machine Vision & Applications，2014，25（5）：1271-1282.

[2]F P Preparata，MI Shamos.Computational Geometry：An Introduction [J]. Texts & Monographs in Computer Science，2015，47（176）.

[3]潘俊，王密，李德仁. 基于顾及重叠的面Voronoi图的接缝线网络生成方法[J]. 武汉大学学报：信息科学版，2009，34（5）：518-521.

[4]Blum H. A Transformation for Extracting New Descriptors of Shape[M]//Wathen Dunn（Eds）.Models for the Perception of Speech & Visual Form. Cambridge，MA：MIT Press，1967：362-380.

[5]周培德，周忠平.确定任意多边形中轴的算法[J]. 北京理工大学学报， 2000，20（6）：708-711.

[6]Weiler K， Atherton P. Hidden Surface Removal Using Polygon Area Sorting [J]. ACM Siggraph Computer Graphics，1977，11（2）：214-222.

[7]刘勇奎，高云，黄有群. 一个有效的多边形裁剪算法[J]. 软件学报， 2003，14（4）：845-856.

[8]王永安，陈萍，杨丰栓，等. 制作高质量天绘彩色正射影像的方法分析[J]. 测绘与空间地理信息，2017（11）：205-206.

[9]Marquardt D W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters[J]. Journal of the Society for Industrial & Applied Mathematics，1963，11（2）：431-441.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。