《图形与几何教学中培养学生推理能力的策略》-理学论文，数学论文-论文范文参考-科学狗论文网

标题

图形与几何教学中培养学生推理能力的策略

范文

黄辉煌

【摘要】在小学数学学习过程中，学生数学推理能力的培养非常重要.推理能力可以锻炼学生的数学学习思维，开阔学生的数学视野.良好的数学推理能力也是解决数学问题的关键因素.笔者结合自己的一线教学实际情况，对小学生数学推理能力的培养提出了一些看法，希望能为广大一线教师提供参考.

【关键词】小学数学;推理能力;培养;策略

一、背景分析

落后理念和评价欠缺引发“短视”：日常教学中，很多教师还未真正理解现代教育理念，他们一直处于应试教育影响下，认为让学生掌握知识即可，其他方面不纳入考虑范围.之所以会出现这种情况，主要是因为教师未能从正确的角度看待教学工作.有些教师的眼中通常只有数学教学内容，他们很少意识到数学思想的存在和学生基本能力的培养.除此之外，对学生进行评价也是教学工作的重要组成部分，然而即使处于新课改环境下，依然存在“评价”问题，即“双基”，这是我国传统评价方式，其所产生的影响至今还存在.评价导向在此方面也有着极大的影响，很多教师以此作为忽视培养学生数学能力、基本能力的借口，久而久之就形成了“短视”，这使学生在数学学习中的推理能力一直没有得到有效提升.此外，新课程改革明确指出小学数学教学应达到“两个权重”，即应该注重演绎推理和合理推理，不可再出现将教学重点集中在证实已经存在的结论上，而忽视探索过程的情况.然而，许多教师在实际教学中未能做到这一点.

二、小学生的数学推理能力培养策略

基于以往的教学经验，笔者以图形和几何知识为例，建立了培养学生合理推理能力的相关策略框架，即阶段差异化实施策略、类别针对性实施策略以及教学优化的实施策略.

（一）基于年段差异，实施渐进式、差别化的培养策略

新课标针对此方面曾做出说明，即数学教学中，推理占据着十分重要的地位，可以说是贯穿始终，然而推理能力并不是一朝一夕能够获得的，其需要较长时间的沉淀，以及教师的悉心指导.为了更好地实现这一目标，从小学阶段开始，教师应将推理能力融入课堂教学中.值得注意的是，小学生的年龄差异较大，同样的教学方式无法满足所有阶段的学生，因此差异化教学应根据学生的低、中、高三个阶段的实际情况而定.

1.小学低段：引导学生感受推理过程

低段的学生以简单推理为侧重点，即“非黑即白”.以图形与几何为例，教师可以最简单的方式开展教学，即为学生展示图形，并让学生自行分辨.此过程要兼具顺序与条理，最重要的是，教师应使学生养成利用自己的语言将推理过程讲出来的习惯.

[案例1]材料的个数

出示材料：●○●○○●○○○●（? ）●○○○○○，括号内应填（? ）球，要填（? ）个.

感受 1：颜色推理.让学生用自己的语言描述，感受判断依据.

感受 2：个数推理.根据规律判断个数，感受判断过程.

感受 3：适当抽象.教师引导学生用类似“1、1、1、2、1、3…”的方式逐渐感受“黑球永远是一个，白球逐渐增加”的分配规律.

在较低阶段，推理仍处于启蒙阶段.

2.小学中段：引导学生学习和体验合理的推理方法

在小学低段学习的基础上，此階段学生的学习能力有所提高.但是，教师要注意，在教学过程当中要循循善诱，循序渐进.

[案例2]具有相同周长的矩形的面积变化规律

出示材料：有一根40厘米细绳，将其围成长方形，边长是整厘米数，如何得到最大面积的长方形？

教师以“独立思考—枚举比较—猜想验证—获取方法—促进应用”的方式组织教学.

其优势之一在于能够让学生将自己的学习成果得以具体应用，同时能够以结果作为事实基础，使后续学习事半功倍.

3.小学高段：指导学生使用“有问题”的推理来解决问题

在小学高段，教师要指导学生充分利用生活经验、现有的数学知识和推理方法，独立推理和解决问题.

[案例3]问题出发的合情推理

基本材料：自行车通过这座桥，车轮转了几周？

师：单凭问题，猜想已知条件是怎样的.

生：桥长和车轮直径可以是已知的.

师：解决这个问题，算式可能是什么？

生：可能是大桥长度 ÷ 车轮周长.

师：如果用 2000÷（3.14×0.6）解决这个问题，你有什么推测？

生：2000是桥的长度，0.6是车轮的直径，整个算式是车轮转的周数.

这个案例激发学生从问题进行反思.相较于教师常用的“例题讲解—获得方法—练习巩固”这样固定的“单行线教学方式”，本案例所实践的“提出问题—合情推理—解决问题”这种反向结构可使共同的“前进教学，反复实践”成为“双向建构”.

（二）基于类别特点，实施针对性、相融合的应用策略

合理推理可分为两类，一类是不完全归纳推理;另一类是类比推理.在教学中，教师既要考虑学生的特点，又要考虑教学内容的特点，同时不能忽视合理推理的特点.只有这样，才能够充分保证教学效率.

1.不完全归纳推理的应用策略——厚积薄发

所谓不完全归纳，其主要是以部分对象为目标，通过对其的推理来向全部对象过渡.这种方法的优势在于学生通过自主思考获取新知识，同时明白过程的重要性.但要注意以下两点：

（1）学生养成在生活和学习中仔细观察的习惯.

（2）学生应善于发现问题，积极探索，并与教师、同学交流.

[案例4]矩形区域计算方法（不完全归纳推理）

在方格中自由地涂出一个或几个长方形，并记录下来.

教师要求学生在方格上画画，并与学生分析长方形的构成，以便使学生更深入地了解长方形区域的计算公式.

2.类比推理的应用策略——瞻前顾后

类比推理是一种特殊的推理方法.当学生遇到新问题时，可以考虑相关的“前”知识.教学时要注意以下两点：

（1）收集尽可能多的属性，并积极探索两个知识之间的共性.

（2）注意差异分析并获得最全面的知识.

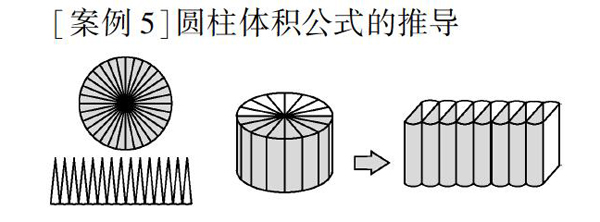
[案例5]圆柱体积公式的推导

学生在学习中要具备举一反三的能力，在学习圆柱体积公式推导的过程中，除了巩固平面图形的面积推导以及学会立体图形的面积推导外，其他相关问题也要有所思考.

（三）基于教學优化，实施有预设、重体验的教学策略

教师在培养学生推理能力的过程中，采用适当的教学方法也是至关重要的.一般来说，教师在课堂教学中培养学生的推理能力应该由浅入深，慢慢推进.

1.基于课堂教学的整体优化，培养学生推理能力

[案例6]自编教材：局部关系推理整体关系

（1）初步感受

如下图，正方形的边长是8厘米，求图中阴影部分的面积.

学生解答：a.8×2-3.14×42;b.8×2-22×4;c.8×2-3.14×12×16.观察思考：不计算，对结果有什么猜想？

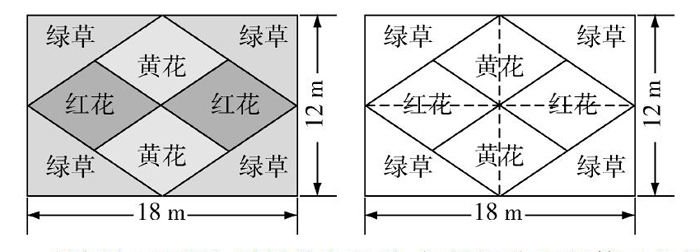
（2）同类再现

校园里有一块长方形的地，学校想种上红花、黄花和绿草.其中一种设计方案如下图所示.你能分别算出红花、黄花、绿草的种植面积吗？

教师出示习题，引导学生反思：如果绿草面积等于花的总面积，这种设计方案是否可用？

2.基于课堂教学的局部优化，培养学生的推理能力

（1）仔细设计材料并创建推理平台

[案例7]推理图形与算式之间的联系

提问：有一个矩形和两个公式，请猜猜它们之间有什么联系？

教师故意预设“空白”，激励学生根据现有信息进行推理，培养空间观念，增强推理能力.

（2）引导观察猜想，激发合情推理欲望

在“图形与几何”的教学中，教师要注重引导学生用数学的眼光观察，看到表面背后的含义，并引导学生主动猜想，激发其进行合情推理的欲望.

三、结束语

推理能力是学生学习数学的重要组成部分.基于本研究成果和困惑，笔者将在“数与代数”等领域开展进一步研究，期待在培养小学生合情推理能力方面获得更完整的认识和实践策略.

【参考文献】

[1]梁仁东.合情推理在小学数学四个领域中的应用[J].海峡科学，2013（7）：95-96.

[2]袁志祥.合情推理在小学数学中的运用[J].教育艺术，2013（5）：70.

[3]陈祥彬.在小学数学教学中培养学生的合情推理能力[J].小学数学教育，2012（11）：7-10.

[4]曹培英.小学数学合情推理的教学研究[J].小学数学教师，2015（Z1）：8-15.

[5]王晓利.小学生合情推理能力培养的策略研究：以五、六年级为例[D].南京：南京师范大学，2011.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。