《求“点面距离”常用的几种基本方法》-理学论文，数学论文-论文范文参考-科学狗论文网

标题

求“点面距离”常用的几种基本方法

范文

潘继军

【摘要】本文结合高考题研究了求解“点到平面的距离”的四种基本方法——直接法（也称定义法）、转移法、等体积法、空间向量法.

【关键词】点面距离;基本方法

计算“点到平面的距离”是历年高考的热点和重点，下面就以高考试题为例探求求解“点到平面的距离”的基本方法.

一、直接法（也称定义法）

即直接找出或作出“点面距离”，按“一找、二证、三计算”的步骤完成，用此方法的关鍵在于如何找出或作出这一垂线段.

二、转移法

转移法是指将此点到平面的距离转化为求另一点到该平面的距离.在直接法不易求解时，可考虑以下转移法：

（1）“点面距离、线面距离、面面距离”间的相互转化——利用与平面平行的直线上各点到该平面的距离都相等的性质进行转化;或利用相互平行的两个平面，其中一个面上的各点到另一个面的距离都相等的性质进行转化.

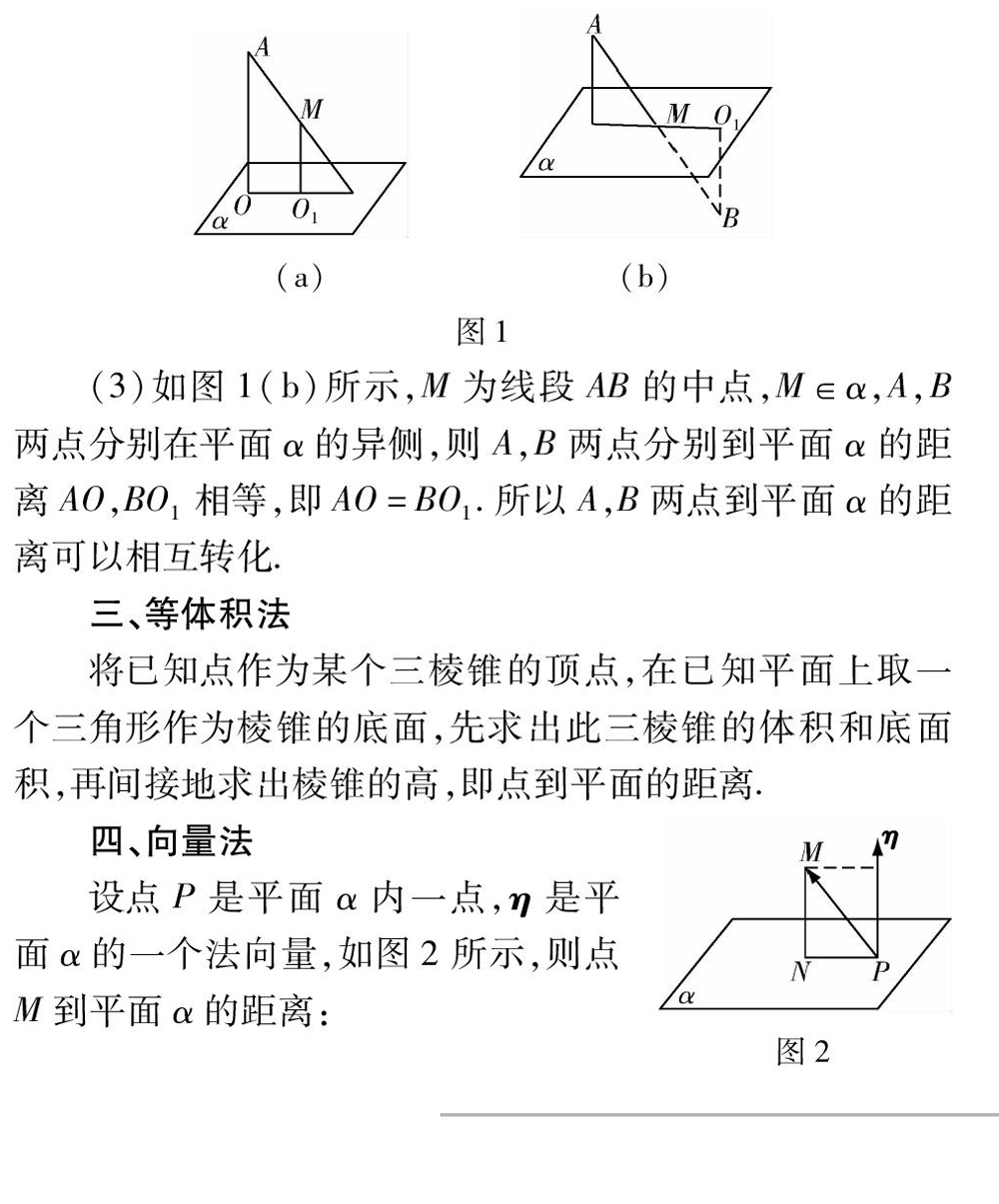
（2）如图1（a）所示，线段AB上的一点B∈α，Aα，M是线段AB的中点，那么A点到平面α的距离AO是M点到平面α的距离MO1的2倍，即AO=2MO1，这样就可以将A点到平面α的距离转化为求M点到平面α的距离（或者反之）.

【参考文献】

[1]杨天勇.巧用向量求空间距离[J].数学学习与研究，2009（11）：83.

[2]李云侠.点到平面距离求解策略[J].高中数理化（高二版），2008（12）：32.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。