《近五年高考命题融入数学文化特点及趋势研究》-教育论文，中小学教育教学-论文范文参考-科学狗论文网

标题

近五年高考命题融入数学文化特点及趋势研究

范文

王悦金美月

摘要数学既赋有理性精神，又具有独特的人文魅力。普通高中数学课程标准及高考考试大纲中明确提出要增加体现数学文化的试题。以近五年融入数学文化社会层面和情感层面的29道高考试题作为研究对象，分析试题中融入的数学文化的变化趋势及特点，可以厘清高考命题融入数学文化的现状并为我国后续高考题的命制提供帮助。

关键词数学文化高考命题特点趋势

数学文化包含四个层面：意识形态层面，即数学信念;社会层面，即数学知识及其变化与发展、民俗数学、数学与其他学科的关系;情感层面，就是数学态度、数学精神、数学美;技术层面，也就是数学思想、方法及其应用[1]。

《普通高中数学课程标准（2017年版）》的命题建议中已明确指出，高考题的命制应注重融入数学文化[2]。而且，近几年的《普通高等学校招生全国统一考试大纲》（以下简称《考试大纲》）中也提出，要展现数学的科学价值和人文价值，体会数学的美学含义等要求[3]，特别是在《2017年普通高考考试大纲修订内容》（以下简称《修订》）中明确提出要增加数学文化[4]。显而易见，数学的文化价值不容忽视。笔者查阅近几年相关高考命题融入数学文化的研究发现，大部分研究要么选取某一年的高考题为对象，分析其试题中如何融入数学文化[5-8]，要么从一道高考题出发，深入分析相关数学知识的演变与发展[9]，缺乏横向的系统研究，以及高考命题中融入数学文化的特点、规律及其趋势的研究。为此，笔者选取了融入数学文化的社会层面和情感层面的高考题进行了研究并提出了几点建议，希望为我国后续高考试题命制提供一些帮助。

一、研究对象

研究范围为2016—2020年各省市（地区）所有版本的高考试卷共73套，其中2016年19套，2017年15套，2018年、2019年和2020年各13套。

根据上述界定，笔者从73套高考卷试题中筛选出了蕴含数学文化社会层面与情感层面的试题共29道作为最终的研究对象。

二、分析与结论

（一）社会层面

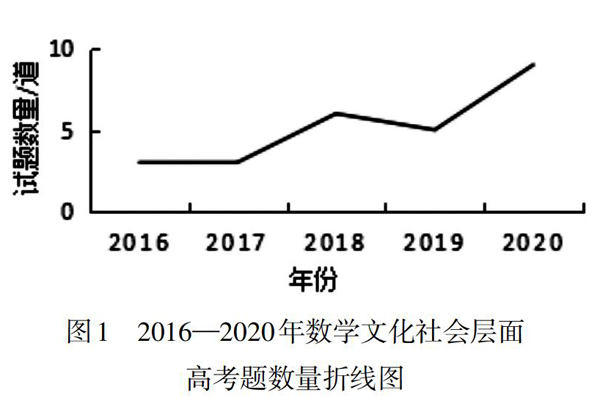
1.总体趋势。（1）试题数量逐年增多。在2016—2020年间融入数学文化的29道高考题中，蕴含数学文化社会层面的试题占绝大多数，共26道，试题数量统计如图1所示。虽然自2016年起，全国每年高考卷版本越来越少，但是从图1可以看出，蕴含数学文化社会层面的试题数量由2016年的3道往后逐年增多，虽然在2019年稍有减少，但是整体仍呈上升趋势。尽管未达到每一版本高考卷中均有设置数学文化试题的程度，仍然有越来越多版本的高考卷积极回应《修订》中提出的增加数学文化的要求。（2）试题融入数学文化社会层面的维度趋于多元化。数学文化的社会层面包含三个子维度：数学知识及其变化、发展;民俗数学;数学与其他学科的关系。据此，笔者对近五年蕴含数学文化社会层面的26道高考题进行了梳理（见图2和图3）。

在近五年来融入数学文化社会层面的高考题中，有关数学知识的变化与发展的相关命题始终保有一定的热度。从图2可以看出，每一年均有相关高考题通过体现数学知识的变化发展来渗透数学文化。从图3可以更清晰地看出，近两年来，其热度有所降低。与此同时，体现数学与其他学科联系的相关数学文化命题热度骤升。更值得注意的是，自2019年来，民俗数学首次出现在数学文化社会层面的命题维度中，并且热度不减。这表明，近年来数学高考命题越来越注重考查蕴含多元文化的数学，注重把数学与中华优秀传统文化相结合，以便更好地体现数学的人文价值。

2.命题特点。（1）体现数学知识的变化与发展。在26道体现数学文化社会层面的高考题中，有12道是以数学知识的变化与发展为背景，并且多为选择题和填空题（见表1）。

由数据分析可以看出，近五年高考题中出现数学文化较多的是代数，其次是几何。以下笔者用一道体现立体几何变化发展的高考题来分析其如何融入数学文化。

体现立体几何的变化发展——阿基米德墓碑图案的高考题如下：

（2017年江苏卷 6）如图4，在圆柱[O1O2]内有一个球，该球与圆柱的上、下底面及母线均相切，记圆柱[O1O2]的体积为[V1]，球的体积为[V2]，则[V1V2]的值是_________。

分析：这道题从表面上看是用立体几何体积公式求比例，实际上，如果学生清楚阿基米德墓碑上所刻图形的文化背景及阿基米德的相关伟大发现，问题就迎刃而解了。阿基米德墓的墓碑上刻着一个圆柱，圆柱内有一个内切球，这个球的直径恰好与圆柱的高相等。阿基米德的伟大发现就是图中圆柱的体积是球体积的3/2，圆柱的表面积也是球表面积的3/2。此高考题的数学文化背景即为阿基米德碑文所刻的图形，了解文化背景，即可知答案为3/2。此题较为独特，隐性考查了立体几何相关知识的演变与发展。

（2）体现数学与其他学科的联系。在26道体现数学文化社会层面的高考题中，有9道是关于数学与其他学科联系的，如表2所示。以下筆者用一道体现数学与建筑学联系的相关高考题来分析其如何融入数学文化。

（2018年全国Ⅲ卷文3 理3）中国古建筑借助榫卯将木构件连接起来，构件的凸出部分叫榫头，凹进部分叫卯眼，图5中木构件右边的小长方体是榫头。若如图5摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是（? ）。

分析：此题主要考查数学三视图相关知识，重点考查学生直观想象素养。然而题目并非直奔主题，而是以中国古代建筑结构中木构件的连接为背景，阐述了建筑学中的相关概念，巧妙地把数学三视图相关知识融入其中进行考查。学生在提升自身核心素养的同时，又能领会数学在建筑学中的广泛应用及古代建筑工匠的智慧，进一步体会数学与建筑学千丝万缕的联系。

（3）体现民俗数学。笔者分析近五年数学文化社会层面的高考题，有5道试题体现了民俗数学，整理如下表3：

体现民俗数学——金石文化中的数学高考试题如下：

（2019年全国Ⅱ卷理16）中国有悠久的金石文化，印信是金石文化的代表之一。印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”（如图6）。半正多面体是由两种或两种以上的正多边形围成的多面体，半正多面体体现了数学的对称美。图6是一个棱数为48的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为1。则该半正多面体共有__________个面，其棱长为__________ 。

分析：此题主要考查考生对半正多面体概念的理解，试题并没有直接给出半正多面体的概念，而是从中国古代金石文化说起，将半正多面体从印信文化中抽象出来，体现了半正多面体在中国古代印信文化中的产生与呈现。这表明当时的金石文化极大程度地融入了数学元素。此题是将民俗数学融入试题的典型案例。

（二）情感层面

1.总体趋势。在近五年的29道数学文化高考题中，涉及数学文化情感层面的试题数量较少，共3道，其中2017年1道，2019年2道，如图7所示。

数学文化的情感层面即數学美。从每一年的试题数量来看，涉及数学文化情感层面的试题并未呈现出明显的上升或下降趋势，仅在2017年及2019年偶有出现。由此可见，数学文化的情感层面并不是近年来高考题融入数学文化的命题热点。

2.命题特点。笔者把近五年涉及数学文化情感层面的高考题整理如下表4。试题分别体现了数学对称美与和谐美。

体现数学美之和谐美的高考试题如下：

（2019年全国Ⅰ卷理4）古希腊时期，人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是[5-12]（[5-12≈]0.618，称为黄金分割比），著名的“断臂维纳斯”便是如此，此外，最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是[5-12]。若某人满足上述两个黄金分割比例，且腿长为105 cm，头顶至脖子下端的长度为26 cm，其身高可能是（? ）。

A.165 cm?????? ????????????????????? B.175 cm?????? ???????????? C.185 cm?????? ???????????? D.190 cm

分析：此题在形式上虽然较为简单，借助比例关系即可求解。但是命题者把试题放在古希腊时期，人们以拥有“黄金分割比”的人体为美的背景下，还例举古希腊时期的断臂维纳斯雕像。在数学中，“黄金分割比”虽然只是一个比例关系，但是在许多艺术作品和建筑设计中都有广泛的应用。“黄金分割比”体现了数学的和谐之美。

三、启示

笔者通过以上研究认为，未来的数学高考命题从数学文化角度需要思考如下两个问题。

（一）注重与其他学科之间的深度融合

在近五年的数学文化高考题中，体现数学文化社会层面的试题多以数学知识的变化发展为背景，着重考查学生对相关数学知识的掌握情况，对学生综合能力的评价考核存在一定的局限性。近年来，核心素养已成为新时代培育全面发展人才的终极目标，是思维品质、关键能力及情感、态度与价值观的有机整合，具有极高的综合性。这就需要教学评价方式也要随之由单一化评价转为多元化评价。而基于steam理念下的数学与其他学科之间的整合，使数学不再仅仅是数学，可以在很大程度上提升评价考核的综合性、科学性与整体性[10]。因此，数学文化视域下，融入数学与其他学科的联系的试题更加值得被提倡，从而把数学文化与核心素养的评价有机整合，相互交融。

例如，2020年全国Ⅲ卷文4理4的高考试题表述如下：Logistic模型是常用的数学模型之一，可应用于流行病学领域，有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数[I（t）]（[t]的单位：天）的Logistic模型：[I（t）=K1+e-0.23（t-53）]，其中[K]为最大确诊病例数。当[I（t*）=] 0.95时，标志着已初步遏制疫情，则[t*]约为多少（ln19[≈]3）。此题描述了Logistic数学模型应用于流行病学调查研究的案例，试题本身不仅把数学与流行病学的联系作为情境呈现，也关注数学模型在流行病学领域的应用。学生在解题的过程中，能够在认识数学知识与其他学科有广泛联系的同时，领悟用数学的思维去思考和解决实际问题，从而感受数学学科真正的意义。这种深度体现数学文化中数学与其他学科联系的高考题，在后续高考题的命制中值得被提倡与保留，这样才能更好地体现数学的学科价值。

（二）体现更多的数学语言美、简洁美

经研究发现，在近五年体现数学文化的高考题中，体现数学美的试题是少之又少。《考试大纲》中已明确把体会数学的美学含义作为考查学生个性品质的基本要求之一[3]。因此，体现数学美的高考题理应被重视。此外，在为数不多的体现数学美的高考题中，从数学的对称美角度出发设计的相关考题居多。显然，这对于数学美的理解过于片面。除了对称美以外，数学美还包括数学的语言美、简洁美、和谐美、辩证美等。众所周知，数学符号具有高度的抽象性、表达的精准性和逻辑的严谨性。这就使数学语言不同于其他语言，它的表达形式独具一格。也正是因为数学语言的特性，使之具有统一、简洁、和谐的美学特征。因此，笔者建议在后续命题中，命题者还应把目光聚焦于数学语言之美。

笔者对上文提到的“2019年全国Ⅰ卷理4”高考题关于“黄金分割比”的数学表达进行分析，原题采用了大家最熟悉的数学语言，将其表达为[5-12]。[5-12]作为一个数学表达式，是学生在数学学科学习中习以为常的数学语言，并常常被当作数字来看待。实际上黄金分割比[（φ）]还可以用诸如此类的数学语言来表达：

[φ=11+11+11+…]或[φ=1+1+1+1+…]

如果在题目表述的适当位置，在不增加试题难度的前提下，把上述的数学语言表达作为数学文化背景来处理，会给人以超脱惯性思维的形式美感。学生在答题过程中，会惊叹于數学语言的奇妙精美之处，体会数学语言的美学含义。数学之美无处不在，数学的语言美是数学的本质美之一。由于高考是一种具有激励和引导功能的评价方式，因此，命题者在后续高考题的命制中，仍需开拓创新融入数学文化的方式、方法，引导学生学会用数学语言表达世界，使数学肩负理性精神的同时，不断彰显其独有的人文魅力。

[参考文献]

[1]金美月，李畅.数学文化内涵探析[C].大连：数学文化进课堂：意义、路径与展望国际论坛，2019：1-2.

[2]中华人民共和国教育部.普通高中数学课程标准（2017年版）[S].北京：人民教育出版社，2018：10-83.

[3]中华人民共和国教育部考试中心.2019年普通高等学校招生全国统一考试大纲[EB/OL].（2019-01-31）[2020-06-06].http：//gaokao.neea.edu.cn/html1/report/19012/5786-1.html.

[4]中华人民共和国教育部考试中心.2017年普通高考考试大纲修订内容[EB/OL].（2016-10-10）[2020-06-06].https：//gaokao.chsi.com.cn/gkxx/zc/moe/201610/20161010/1559590536.html.

[5]张畅畅.数学文化在高考真题中的渗透：以2019年高考真题为例[J].数学学习与研究，2020（8）：3-5.

[6]张金传.数学文化的六种常见高考题型及教学策略：以2018年高考试题为例[J].中国数学教育（高中版），2019（10）：49-53.

[7]王国学.2017年数学文化高考题赏析及教学建议[J].高中数学教与学，2018（2）：42-44.

[8]仓万林，史嘉.随风潜入“卷” 润“题”细无声：谈湖北高考题的文化韵味及教学建议[J].数学通报，2015，54（6）：46-50.

[9]马进才.从一道“卡西尼卵形线”高考题看“数学文化”[J].中学数学研究（华南师范大学）：上半月，2017（7）：44-46.

[10]袁磊.核心素养视域下STEAM教育的课堂教学变革[J].中国电化教育，2019（11）：99-103.

（责任编辑：赵晓梅）

作者简介：王悦（1995—），女，辽宁沈阳人，辽宁师范大学数学学院硕士研究生，研究方向：数学比较教育研究;金美月（1968—），女，黑龙江佳木斯人，辽宁师范大学教授，博士，研究方向：比较数学教育及教师教育研究。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。