《引导初中生研究数学试题的几个视角》-教育论文，现代教育论文-论文范文参考-科学狗论文网

网站首页词典首页

标题

引导初中生研究数学试题的几个视角

范文

孟艳

摘要：本文引导学生通过归类与总结、延伸与推广、积累变试题组、“去伪存真”、善于观察与发现、积极反思寻求对策等方面研究初中数学试题。

关键词：初中生 ?数学试题 ?思维

引言

数学是培养思维的学科，个人认为在平时的教学中提升学生的思维品质是数学教师的首要任务。因此笔者在自己的教学工作中，力求从如下几个方面引导学生研究数学试题以培养学生的数学思维。

一、归类与总结

每个知识点涉及哪些题型，教师不但要善于总结，而且要指导学生进行归类和总结。比如角的有关题型可总结为角的表示、角的换算及计算、方位角、时针与分针转动问题、角度的计算等。

二、延伸与推广

研究试题的推广目的是培养学生的探究意识和创新精神，但不需要让学生对试题的背景、试题的改编等问题进行深究，对试题的推广也应该量力而为。例如：

如图，抛物线y=ax2+bx+c经过A（-1，0）、B（3， 0）、C（0 ，3）三点，直线l是抛物线的对称轴.

（1）求抛物线的函数关系式;

（2）设点P是直线l上的一个动点，当△PAC的周长最小时，求点P的坐标;

（3）在直线l上是否存在点M，使△MAC为等腰三角形？若存在，直接写出所有符合条件的点M的坐标;若不存在，请说明理由.

此题是在二次函数的背景下研究等腰三角形问题，培养学生分类讨论的思维。教师可在学生做完后让学生自己试着改编第（3）小题，同时在这个二次函数的背景下变换出其他的几何问题，从而实现对几何知识的深度理解。

三、积累变试题组

原题：解方程x-1+x+1=6

变式：（1）解不等式

①x-1+x+1≤6

②x-1+x+1≥6

（2）①x-1+x+1≤a恒成立，求a的取值范围。

②x-1+x+1≥a，求a的取值范围。

由方程到不等式，由具体数字到抽象的字母，在这些变化的过程中把知识串联起来，使学生达到“解一题，带一串，通一类”的境界。以此为契机，引导学生在平时的学习中试着自己对题目加以变化，真正提高数学的思维水平。

四、注意数学中的“去伪存真”

数学中的“去伪存真”，即看到数学问题的本质，抓住解题的关键点。例如：

在平面直角坐标系xOy中，对于点P（x，y），我们把点P（-y+1，x+1）叫作点P的伴随点。已知点A1的伴随点为A2，点A2的伴随点为A3，点A3的伴随点为A4，…，这样依次得到点A1，A2，A3，…，An，…若点A1的坐标为（3，1），则点A3的坐标为 ? ?，点A2017的坐标为 ? ?;若点A1的坐标为（a，b），对于任意的正整数n，点An均在x轴上方，则a，b应满足的条件为 ? ?。

此题目看似信息量很大，但是解题时可根据問题“去伪存真”，留下关键信息即可。①首先，题目要求的是第4n+1项，其他不必探求;②其次，纵坐标都是1，只需探求横坐标。

让学生学会“去伪存真”，是优化思维的有力手段。

五、引导学生多角度观察

以下给出一道数字规律题，其下两种方法均为学生的观察与发现过程。

观察每行最后一个数字会发现：第n行最后一个数为n（n+1），所以第（n-1）行最后一个数字为（n-1）n，即n2-n。因此第n行第一个数为n2-n+1，第（n+1）个数为n2-n+（n+1），即n2+1。

从以上分析可以看出，由于观察的视角不同，学生找到了不同方面的规律，因此给出了不同的解决方法。

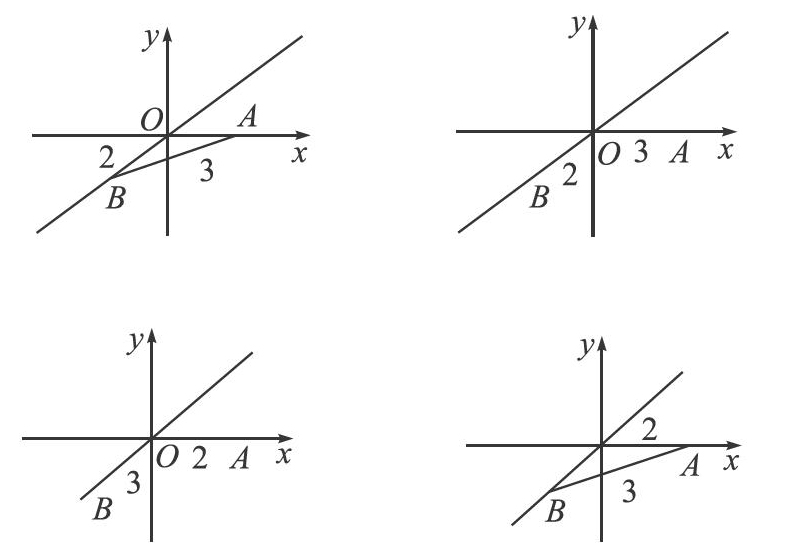
把题目放在平面直角坐标系中，不仅考查到分类讨论的思想，而且在求点的坐标的过程中，可以考查到两点间的距离公式、等腰三角形性质及勾股定理。这道题的背景对学生来说还是比较熟悉的，而且这些知识点也是中考必考的，并且多在小题中出现。为了降低计算及思考的难度，把一条边设置在x轴的正半轴上，另外一条边设置在正比例函数y=x图像在第一象限的部分上。后面的变式1主要是想涉及三角形全等中边边角的不合理性，当边长是2和3的时候，变式1的两种情况是不存在的。而变式2是想进一步提高学生思维的全面性，并提醒学生审题过程中要关注到条件中的细小差别，进而培养学生思维的缜密性。教师改编题目，能够引起学生对数学知识形成和发生过程的关注。

七、学会反思

关于反思从以下几个方面给出对策：

1.对于学生知识性的错误：要看是知识理解出现了问题还是知识使用出现的问题。

2.对于学生逻辑性的错误：要培养学生分析问题的能力，培养逆向思维能力，把条件与结论有效地结合起来。

3.策略性错误的对策：多角度思考问题，多途径解决问题。

作为一名数学教师，我在平时的工作中尽量从以上七个方面引导学生去研究试题，希望借此优化学生的思维品质，培养其思维能力。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。