《初中几何“路径最短问题”的探究与解决策略》-教育论文，课程教育论文-论文范文参考-科学狗论文网

标题

初中几何“路径最短问题”的探究与解决策略

范文

陈隆田

摘要：初中几何“路径最短问题”，近年来备受中考命题的青睐，成为中考数学的热点与考点。本文中笔者对几何“路径最短问题”的原理、路径的类型、起点终点的类型进行分类，运用图形变换，等效点、等效线段的转换，解决“路径最短问题”的策略。

关键词：几何公理;路径最短;图形变换;等效点;线段

中图分类号：G633.7?????????? 文献标识码：A文章编号：1992-7711（2020）10-075-2

2018年全国各地中考数学试卷中频频出现“最短路径问题”，如广西贵港、山东滨州泰安、天津、湖北黄冈……“路径最短问题”涉及知识较多，具有很强生产生活实践应用价值。笔者正视热点，结合自己教学实践经验，细致深入地进行探究，形成自己解决“最短路径问题”策略，教学中借助几何画板的动态化、明晰化优势，使“路径最短问题”专题教学取得良好效果。

“最短路径问题”多以填空题、选择题进行考察，分值4～5分，难易程度为0.1～0.3，属于学生较难掌握、解决的问题。

有鉴于此，笔者将从以下几个方面来探究“最短路径问题”以及解决策略。

一、“最短路径问题”的三个主要理论依据

1.线段最短

公理：连接两点之间的所有连线中，线段最短。简称：线段最短。

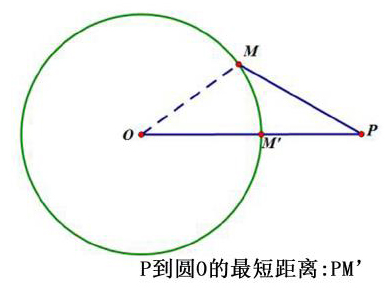
笔者解读：公理“两点”即两个定点，因此，公理为解决两个定点之间最短路径问题提供理论依据。同时，它还能拓展解决，圆外定点到圆周上动点最短距离问题。如下图所示：

2.垂线段最短

公理：直线外一点到直线上所有点的连线中，垂线段最短。简称：垂线段最短。

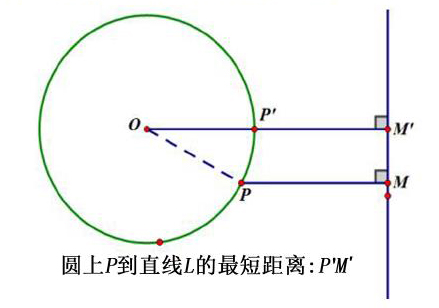
笔者解读：运用本公理能解决直线外一定点到直线上的所有点即直线上动点之间的路径最短问题。同时它还能拓展解决，圆周上动点到圆外定直线的最短距离问题。如下图所示：

3.三角形三边关系定理

定理：三角形两边之和大于第三边，两边之差小于第三边。

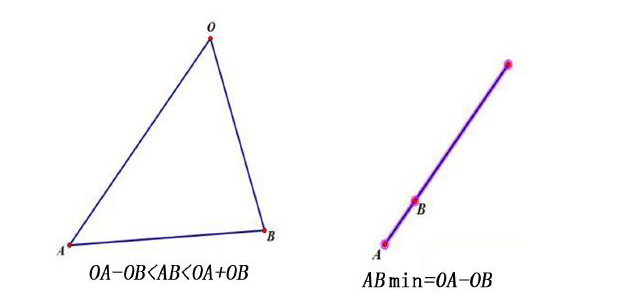
笔者解读：根据该定理，三角形的第三边长度受到一端相连的两条定长线段限制，这也说明了公共端点的两条定长线段的另外两个端点之间的路径距离范围在两条线段之和与之差之间。当两条线段中短的线段完全重合在长的线段上时，线段另外两个端点之间的路径最短距离就是两条线段之差。因此，三角形的三边关系定理的拓展能解决，公共端点的两条定长线段另外两个端点之间的最短路径问题。如下图所示：

二、“路径最短问题”的类型

1.路径类型分类

一条线段、“V”型折线、“Z”型折线、三角形周长型与星型三条线段之和等等。

2.点类型分类

（1）定点+过程性动点+定点;（2）定点+过程性动点+动点;（3）动点+动点

三、解决“最短路径问题”的基本步骤

1.第一步

观察路径类型，确定起点、终点的点类型。

2.第二步

利用图形变换（轴对称、全等、平移、旋转等）对应线段相等性质把路径中某些线段进行等效转换，使原路径变成向两个方向伸展的连续折线，再“拉直”折线。

3.第三步

确定某一定点为路径的起点，根据终点的类型来确定路径最短的理论依据。

四、掌握解决“最短路径问题”的几个“必杀技”

1.关于等效点、等效线段

利用图形变换（轴对称、全等、平移、旋转等）得到对应点、对应线段，由于作用相同、数量关系确定，暂且称为等效点、等效线段，这是实现最短路径有效转换的关键。

2.各种类型路径的分解转换

（1）“V”型折线、“Z”型折线、三角形周长型路径：以过程性动点所在的直线为对称轴，做起始定点的对称点，连接得到等效线段，使“V”型折线、“Z”型路径变换为向两个方向伸展的连续折线，再“拉直”路径。

（2）星型三條线段之和：通过绕其中一个定点将其中一个三角形旋转60o，使之拆解为向两个方向伸展的连续折线，再“拉直”路径。

3.原理判断与选择——关键看起点、终点的类型

（1）如果起点、终点都是定点，那就利用“线段最短”原理。

（2）如果起点是定点，终点是在直线上的动点，那就利用“垂线段最短”原理来解决。

（3）如果起点是定点，终点是在定圆上的动点，那就利用“线段最短”拓展原理来解决。

（4）如果起点是定圆上的动点，终点是在定直线上的动点，那就利用“垂线段最短”拓展原理来解决。

（5）如果公共端点的两条定长线段另外两端的两个点，那就利用“三角形两边之差小于第三边”拓展原理来解决。

4.关于隐形圆的运用

当终点没有明确的运动轨迹时，就要考虑是否在隐形圆上运动。认真挖掘题目的已知条件。如：四点共圆、“直径所对圆周是直角”等方法发现隐形圆的存在。

5.关于几何画板在解决“路径最短问题”中的作用

运用几何画板的动态化、明晰化的优势，能生动形象地呈现路径变换过程，从而提高课堂上解决“最短路径问题”的有效性。

五、具体实例分析

例1：如图，正方形ABCD边长为4，E、F分别是边BC、CD上的动点，BE=CF，连接BF、DE，求BF+DE的最小值。

简析：路径“BF+DE”看似不满足以上任何一种路径，但根据已知条件，连接AE，显然△ABE≌△BCF，得出AE=BF，因此，等价路径“AE+DE”就是“V”型了。由于过程性动点E在直线BC上，所以作A关于直线BC对称点A′，实现A与A′等效，AE=AE′，从而把原来“V”型路径转化向两个方向伸展的连续折线，“拉直”就得到最短距离。由于点类型是“定点+过程性动点+定点”，故利用“线段最短”原理，即A′D为最短路径。本题运用三角形全等、轴对称两种的几何图形转换，实现一条线段的两次等效转化。

例2：如图，在四边形ABCD中，∠DAB=120°，∠B=∠D=90°，AD=4，AB=3，點M、点N分别是边BC，CD上的动点，求△AMN周长的最小值。

简析：本题路径属于三角形周长型，封闭的三条变化的线段需要“拆解”。发现动点M、N分别在直线BC、CD上，所以要分别做定点A关于直线BC、CD的对称点A1、A2，得到AM=A1M，AN=A2N，因此实现封闭的三条变化线段“拆解”向两个方向伸展的连续折线。本题通过两次的轴对称神奇地实现了一个定点对称变出两个定点，故本题点类型真正属于“定点+过程性动点+定点”。

例3：如图，在△ABC中，∠CAB=90°，AB=3，AC=4，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF的中点，求PM的最小值。

简析：本题路径类型是一条线段，点类型是两动点，看似无从下手。认真阅读题意，不难发现：四边形AEPF是矩形，连接AM，A、M、P三点共线，并且MP=12AP，所以AP是MP等效线段，确定线段AP最小值即可。由于线段AP是“定点+动点”，根据“垂线段最短”原理，当AP⊥BC时，求出AP的长度就解决了PM的最小值。

例4：如图，在Rt△ABC中，∠ABC=90°，BC=4，BA=3，动点F在边AC上运动，连接BF，过点C作CE⊥BF于点E，交AB于点D，求A、E两点之间距离的最短距离。

简析：本题路径是一条线段，点类型：定点+动点。由于动点不在直线上运动，所以要研究动点P的运动轨迹。根据题意∠ACB=90°，并且对着定长线段BC。故此，根据“直径所对的圆周角是直角”推导得知E的运动轨迹：以线段BC为直径的圆周。因此可利用“线段最短”的拓展原理解决。连接BC的中点O（即圆心）与A，且与圆交于H，当D运动到H时，AH的长度就是AE的最小值。

例5：在Rt△ABC中，∠ACB=90°，AC=4，BC=3，点D在以点A为圆心，2为半径的圆上一点，连接BD，点M为BD中点，求线段CM长度的最小值。

简析：本题路径类型是一条线段，点类型为：定点+动点。动点M运动轨迹不确定。综合考虑已知条件，取AB的中点N，连接AD、MN、CN，发现MN=12AD，CN=12AB，均为定长，且有公共端点。根据“三角形的三边关系”定理拓展得知，当D运动到使MN与CN重合位置时，CM长度的最小值。

例6：如图，矩形ABCD中，BC=12，AB=4，P是矩形ABCD内一动点，连接PA、PB、PC，求PA+PB+PC的最小值。

简析：本题路径类型是星型的三条线段之和，点类型非常规类型。把其中一个三角形（如△ABP）绕定点A旋转60°。得到△ABP≌△AB′P′和△APP′是等边三角形，从而实现AP=PP′， BP=B′P′。这样原星型的三条线段之和就转化为向两个方向伸展的连续折线，“拉直”后路径本质上是：两定点之间的线段最短。由此可见凡路径为星型的三条线段之和的问题要用旋转60°的方法得以实现路径转化，全等和旋转是实现线段等效转化的“利器”。

本文只是对初中几何“路径最短问题”探究和解决策略的粗浅思考，囿于文章篇幅以及实例材料的局限，对问题研究深度不足，方法策略不够丰富，以期继续深入完善。

（作者单位：福建省福州第三十中学，福建福州 350008）

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。