《开篇谋局》-教育论文，课程教育论文-论文范文参考-科学狗论文网

标题

开篇谋局

范文

王广富王凤灵

【摘要】高等数学是理工科各专业必修的一门重要基础课，也是学好专业课的必备条件。很多同学对数学课有畏难情绪，如何让同学们了解高等数学的内容，提高同学们学习高等数学的兴趣，消除同学们对高等数学的焦虑和恐惧，掌握解决数学问题的方法，第一堂课是学好高等數学的关键。本文通过教学内容切入、教学内容特点和怎么学好高等数学等方面，就如何上好高等数学第一堂课做了相关的探讨。

【关键词】高等数学 ?悖论 ?三角函数

【基金项目】国家自然科学基金（No.11861032）江西省高等学校教学改革研究重点项目（No.JXJG-17-5-1）。

【中图分类号】G642;O13-4 【文献标识码】A 【文章编号】2095-3089（2020）08-0124-02

1.引言

高等数学（Advanced Mathematics）是高等院校一门重要的基础理论课程，是理工和经济管理等非数学专业学生的必修数学课。“它不仅是学好其他专业课程的有力工具，而且对于培养学生的抽象思维能力、逻辑推理能力和解决实际问题的能力起着重要的作用”[1]。但同时数学又由于其自身要求逻辑严密，计算能力要求高，导致很多大学生对高等数学产生了畏难情绪。现在大一新生中流行一句话，流传很广——“从前有棵树，叫高树（数），树上挂了很多人”。说明该门课程挂科率很高，同学们都已经到了怕的地步。那么如何帮助大一新生学好高等数学，克服他们的畏难心理并激发学生的求知欲，就显得尤为重要。作为高等数学老师，必须打破原有的思维定势，建立新的思维结构，帮助学生转变思维，从而充分调动学生的学习积极性。因此高等数学的第一堂课尤其重要，从而必须设计一堂富有启发性和鼓励性的“绪论课”[2]。

2.由悖论引入学习高等数学的必要性

在给学生讲解高等数学内容之前，首先用经典的龟兔赛跑引入悖论“兔子跑不过乌龟”，其次给出另一个悖论“2=”。用这两个悖论来引起学生对数学的兴趣，引发学生们的探讨。

例1：兔子永远追不上乌龟。

假设兔子比较仗义，觉得自己跑得快，就先让乌龟向前爬行s0米。这时，兔子和乌龟再听发令枪响同时跑。设兔子速度为v1，乌龟速度为v2（v1>v2）。显然兔子从它的位置A跑到乌龟的位置B，这段距离s0要花兔子t1=时间，而兔子跑的同时乌龟并没有在B等兔子，而是向前爬到了C处。此时相当于乌龟在兔子前面C处，兔子在B处，两者相距s1米。两者此时同时再跑，当兔子到达C处时，而乌龟又向前爬行了一段距离s2后到达D处。如此重复下去，虽然兔子与乌龟之间的距离越来越短，但是两者之间始终有差距，故兔子永远追不上乌龟。

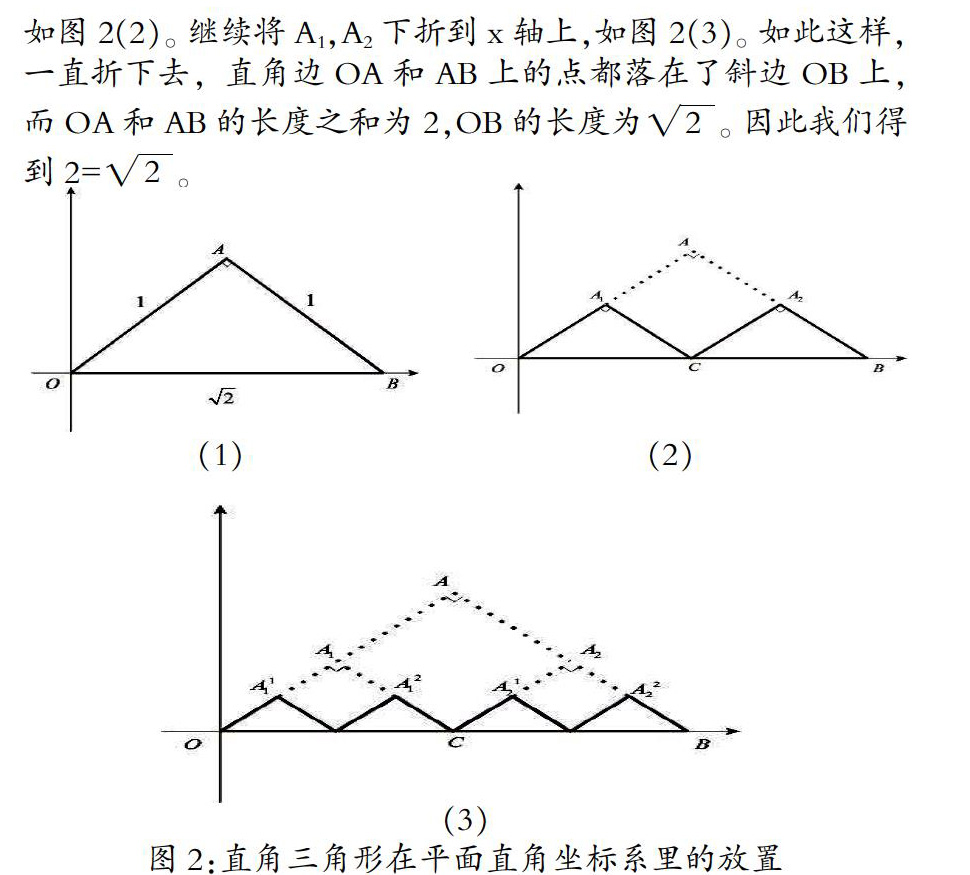
假设将直角边长为1的等腰直角三角形的斜边放在x轴上，如图2，则|OB|=。将A点向下折到x轴上，设为C。如图2（2）。继续将A1，A2下折到x轴上，如图2（3）。如此这样，一直折下去，直角边OA和AB上的点都落在了斜边OB上，而OA和AB的长度之和为2，OB的长度为。因此我们得到2=。

两个悖论都是基于将有限的线段进行了无限次的划分。涉及到无穷多个数的和的问题，而不再是单纯初等数学所考虑的有限问题。怎么解决这个问题呢，这就依赖于我们要学的高等数学。

3.中学数学与高等数学的衔接

由于新课改的问题，原来很多中学学习的内容现在已经弱化甚至不做要求，但是到了高等数学里又要求很高。而原来是高等数学的内容又放在高中讲解了一部分，例如导数和定积分。这就要求大学数学老师对整个高等数学内容给学生一个轮廓，高屋建瓴，能够指导学生哪些内容应该重点补齐，而哪些东西又与高中所学不同。这些都需要老师认真指出来。作者认为学生补全掌握三角函数的知识，主要有：1）正割函数和余割函数;2）同角间的三角函数关系;3）诱导公式;4）积化和差与和差化积公式。

尤其是第一和第四部分对于学生来讲是新内容，要求学生学会，记住并灵活掌握。

1）正割函数和余割函数的引入。

设是一个任意大小的角，将角？琢的顶点放在坐标原点，始边放到x轴上，角？琢的终边上任意一点的坐标是P（x，y），它到原点的距离为r。（见图3）。则角？琢的正弦，余弦，正切，余切定义如下：

2）同角间的三角函数关系。

积的关系：六边形上每个顶点的三角函数值等于它相邻的两个三角函数值的乘积。例如：sin=tan·cos。

平方和关系：实边构成的三角形中，上面两个顶点处的三角函数值的平方和等于下面顶点处三角函数值的平方。例如：tan2+12=sec2。

3）诱导公式。这个公式是中学里重点内容，学生一般掌握较好，只要给学生点到即可。

4）和差化积与积化和差公式。

和差化积公式看起来很复杂，但是观察其特点，只要记住每个公式的前后三角函数名称即可，因为后面两项里的角度分别是前面两个角的和的一半与差的一半。

4.如何学好高等数学

4.1高等数学的特点

高等数学作为一门科学，经过三百多年的发展，有其固有的特点，高度抽象，理论系统严密，逻辑性强，应用性广。高等数学无论概念、性质和定理，还是判断和推理，都要运用逻辑的规则，有严密的逻辑性，遵循思维的规律。数学是自然界的语言，是自然科学与社会科学的基础，为其他学科提供思想、观念和研究方法。数学也是一种文化，在人类文明的进程中起着重要的推动作用。人类历史上几乎所有的原始创新和重大发现都同数学的发展与进步密切相关。尤其是到了现代，随着电子计算机的出现，使得数学的应用领域更加宽广，现代数学正成为科技发展的强大动力。因此，学好高等数学对我们来说相当重要。

4.2 学习高等数学的方法

针对高等数学的特点，要学好高等数学，重要的还是要：

1）充分理解概念。高等数学中有很多定义和概念。概念反映的是事物的本质，所以一定要弄清楚它是如何定义的、有什么性质，通过做相应的练习巩固知识，才能真正地理解一个概念[4]。

2）完全掌握定理。对于课本上的每个定理都要掌握它的条件是什么？结论是什么？记住适用的条件和适用范围，做到有的放矢，千万不要“张冠李戴”，“乱点鸳鸯”。

3）弄懂例题，多做练习。课本上的例题都是很典型的，有助于理解概念和掌握定理[4]。针对不同的例题，根据其特点，熟悉其解法，在理解例题的基础上作适量的习题。作题时要善于总结题型和解题方法，这是因为大学学习与高中学习是完全不同的状态，高中时可能一个知识点会做很多练习来巩固，高等数学教学内容多，有时候老师一堂课可能就会讲很多知识点，但是留给学生练习的时间又比较少，所以学生课下一定要多做练习，做完之后还要反思，举一反三，“勤能补拙是良训，一分辛苦一分才”。

4）理清内容，把握脉络。要对每个章节的内容及时总结，对所学的知识体系有整体的把握，“会当凌绝顶，一览众山小”，这样不仅可以加深对知识的理解，还会对进一步的学习有所帮助。

结语

好的开始是成功的一半，上好第一堂课对老师和学生都具有重要的意义。正确的引导学生，使学生充分认识到学习《高等数学》的重要性和必要性，調动学生的积极性，从而对这门课产生较浓厚的学习兴趣，也就为学好这门课奠定了基础。

参考文献：

[1]上海交通大学数学系，高等数学[M]，上海：上海交通大学出版社，第三版，2012.

[2]刘俊，刘佳.“绪论课”——打开《高等数学》殿堂的金钥匙，科技资讯，2011， 212.

[3]杨文兰.同角三角函数关系教学之我见，涪陵师专学报，1999年第15卷第3期，58-60。

[4]高等数学http：//www.worlduc.com/blog2012.aspx？bid=27

926175

作者简介：

王广富（1976-），男，山东菏泽人，博士，华东交通大学理学院副院长/副教授，2016.3-2017.2英国伯明翰大学访问学者，主要从事大学数学教学及图论方面的研究。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。