《新中考背景下初中数学“好题”例析》-教育论文，课程教育论文-论文范文参考-科学狗论文网

标题

新中考背景下初中数学“好题”例析

范文

潘振南

摘要：本文及本课题所说的“新中考背景”，指从2017年开始以来的福建省中考统一命题、统一考试等中考改革的新背景，本次新中考改革强调落实“立德树人”的根本任务，强调中考命题要符合义务教育特点，要有利于发展学生的核心素养，要重视考查学科知识的综合应用能力，考查学生的创新意识和创新能力。本课题所说的“初中数学考试”，指初中学段数学科的各种考试，包含课时小测、章节考试、期中考试、期末考试、毕业考试、升学考试。本课题所说的“命题导向研究”，指从命题的指导思想、基本原则、考试内容、试题结构、试卷难易度等方面随着新背景、新时代的变化而进行指导性、方向性的研究。本课题组经过一年多的探索研究，收集积累了一些“好题”。

关键词：初中数学;好题例析;立德树人

中图分类号：G633.6 ? 文献标识码：A ? 文章编号：1992-7711（2019）09-0123

对初中数学教师来说，深入研究命题导向，是教师反思自身教学行为、改进教学方法的重要环节之一。因为大家都知道，初中数学学习是以“题”为载体的，处在教育一线的数学教师要善于围绕教学的主线和每节课的核心内容，精选“好题”、改编“好题”;要善于从数学知识的相互联系及学生的认知规律出发，用好题、巧解题、多变式，要充分发挥教师的主导作用，突出以问题设计为数学教学设计的重点，让学生少做题、轻松学、有兴趣，最终培养学生学会数学思考。教师要研究“数学好题”，可从不同的课型、课后作业及各级各类考试等设计中不断积累和总结经验。

一、初中数学“好题”的理论标准

《义务教育数学课程标准》（2011年版）明确指出：数学课程评价的根本目的是为了促进学生学习，改善教师教学。命题应发挥数学课程评价的多种功能。数学考试命题的出发点和归宿应该是促进学生的发展，试题要给学生的生命舒展、个性发展留下空间，从内容到形式都要朝着有利于学生发展的方向变革，这样的试题才具有效度、信度。就新中考背景下评价一道初中数学题是否为“好题”的理论标准，笔者认为可以归纳以下几个要点。

1. 科学性原则：试题内容符合科学性，没有出现科学性的错误，没有涉及到学术上的争议;

2. 规范性原则：试题编制符合规范性，题型使用得当，叙述表达规范，版面格式规范;

3. 公平性原则：试题素材、背景材料等的使用公平（比如城市与农村学生均能接受的情景、素材）;

4. 导向性原则：试题导向明确，能体现近几年中考数学命题改革的变化趋势;

5. 思想性原则：试题能体现数学思想方法的考查，体现数学的教育价值观和数学的文化性的考查;

6. 创新性原则：试题在背景、形式、内容或解答方法等方面具有一定的新颖性与独特性，能诊断考生的数学创新意识与创新能力。

二、初中数学“好题”的特征例析

初中数学教学本身就有不同情境，在不同情境中用不同的题，其教育教学的价值、效益就不同。同一道题，在不同情境中的教育教學价值、效益也不一样。因此，笔者认为所谓的“数学好题”，撇开具体的题型，就是试图找到一种大家都能接受的相对合理的“数学好题”的一些基本要素。现例析数学“好题”所具备的一些特征。

1. 关注课标教材，重视基础考查

一道好试题不一定就是一道难度很高、很完美的题目。例如，每年的各地市质检卷及中考卷等综合卷都会突出对基础知识、基本技能、基本思想及基本活动经验的考查，选择题、填空题、解答题这三种题型的前半部分一般情况下都是基础题中的容易题，绝大多数学生都能得分，这些试题注重通性、通法，淡化特殊技巧，较好地体现了基础性、公平性及普及性，这里就不一一举例了。

2. 关注核心素养，渗透思想方法

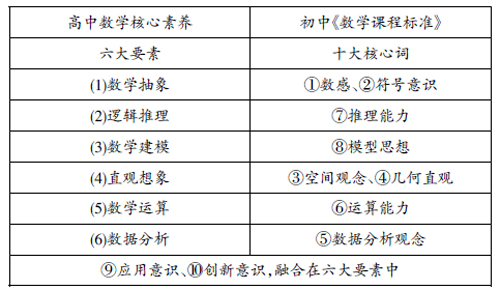
高中数学的核心素养与初中《新课程标准》的核心素养对比，如下表所示：

《初中数学课程标准（2011年版）》中提出的10个核心概念指向学习主体（学生）的特征，是学生在义务教育阶段的数学课程中最应得到培养的数学素养。从初中数学学习内容的特点与要求出发，结合近几年中考数学命题的变化趋势，我们应当将数感融入运算能力，将符号意识融入模型思想，进而将空间概念、几何直观、数据分析观念、运算能力、模型思想、应用意识、创新意识作为初中阶段“好题”编制的关注点。

（1）空间观念

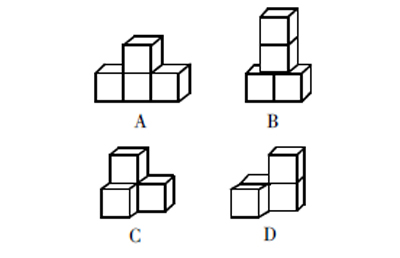
例1：下面的几何图形是由四个相同的小正方体搭成的，其中主视图和左视图相同的是（ ?）。

评析：本题考查简单几何体三视图，属于基础性知识的考查，由课本习题改编而来，但不是单纯地让学生识别一个几何体的某一种视图，而是综合考查学生的空间观念。

（2）几何直观

例2：若数a使关于x的不等式组<5x-2≥x+a有且只有四个整数解，则a的取值范围是________。

评析：本题没有给出数轴，其目的是希望学生能够自觉地画出数轴，考查学生对“见数思形”的敏感性。利用数轴求不等式组的解集，有利于学生通过直观性探索解决问题。

（3）运算能力

例3：先化简÷（-x+1），然后从-

评析：本题属于分式的混合运算，同时考查了分式的意义。运算能力要求为第二级水平，这是一种常见的题型，也是本省这两年中考都考到的题型。本题考查学生运算能力的水平，主要表现在两个方面：一是在根据定义、公式、法则等进行数学运算过程中呈现出来的正确、合理、灵活和熟练程度;二是对运算的理解和寻求合理简洁的运算途经解决问题的水平。

（4）推理能力

例4：在不透明的袋子中装有一个几何体模型，两位学生摸该模型并描述它的特征。

甲同学：它有4个面是三角形;乙同学：它有8条棱。

该模型的形状对应的立体图形可能是（）。

A. 三棱柱 ? ? ?B. 四棱柱 ? ? ? ?C. 三棱锥 ? ? ? D. 四棱锥

评析：数学的每个分支都充满了推理，所以考查学生推理能力的载体是全方位的。而考查空间观念，也可以用排除法，比如本题：三棱柱只有两个三角形的面，所以排除A;四棱柱没有三角形的面，所以排除B;三棱锥有四个三角形的面，但是只有6条棱，所以排除C;剩下D选项，且四棱锥符合条件，故选D。

例5：已知二次函数y=ax2+bx+c中，其函数y与自变量x之间的部分对应值如下表所示：

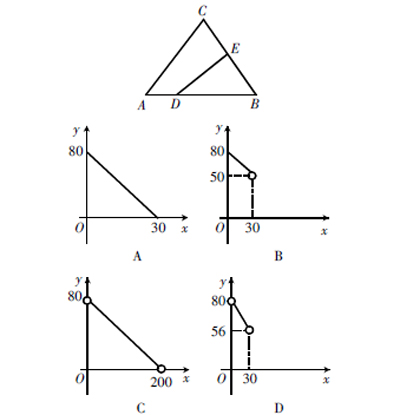
点A（x1，y1）、B（x2，y2）在函数的图像上，则当1

A. y1>y2 B. y1

评析：本题的背景材料是初中数学中的重要内容——二次函数。先由表格中的数据可以推出该二次函数开口向上，且对称轴为直线x=2，再由函数的单调性可以得到答案。本题选择值的设置很严谨，等号取不取的问题必须重视。

（5）模型意识

例6：如下右图，在△ABC中，AC=BC=25，AB=30，D是AB上的一点（不与A、B重合），DE⊥BC，垂足是点E，设BD=x，四边形ACED的周长为y，则下列图像能大致反映y与x之间的函数关系的是（ ? ? ）。

评析：本题综合考查函数的图像、等腰三角形的性质、相似三角形的判定和性质等知识点，解题的关键是利用相似构造方程表示出DE和BE，再利用周长公式构建函数关系式。本题如果改为一道解答题（如：求出y与x之间的函数关系并画出图像）效果可能会更好，因为选择值的设置，由自变量的取值范围可以直接舍去A、B、C三个答案。

（6）应用意识

例7：建筑工人砌墙时，经常在两个墙脚的位置分别插一根木桩，然后拉一条直的参照线，其运用到的数学原理是（）。

A. 两点之间，线段最短

B. 两点确定一条直线

C. 经过一点有无数条直线

D. 以上均不正确

例8：如下图，小明到小颖家有四条路，小明想尽快到小颖家，他应该走第______条路，其中的数学道理是____________。

评析：例7、例8这两题从生活现象入手，揭示看似简单且习以为常的行为背后有着深刻的数学原理，考查学生利用已学的数学知识解决实际问题。类似的，在初等数学中，大量的数学知识都具有现实背景，如三角形的稳定性等，都提供了从数学的角度解释生活现象的鲜活的命题素材。

（7）创新意识

例9：定义：如果一个数的平方等于-1，记为i2=-1，这个数i叫做虚数单位，把形如a+bi（a，b為实数）的数叫做复数，其中a叫这个复数的实部，b叫做这个复数的虚部。它的加、减、乘法运算与整式的加、减、乘法运算类似。

例如计算：（2-i）+（5+3i）=（2+5）+（-1+3）i=7+2i;

（1+i）×（2-i）=1×2-i+2×i-i2=2+（-1+2）i+1=3+i;

根据以上信息，完成下列问题：

①填空：i3=________，i4=________;

②计算：（1+i）×（3-4i）;

③计算：i+i2+i3+…+i2017。

评析：本题向初中学生提出了一个新的概念——复数，约定了一种新的运算，通过创设全新的问题情景，要求学生通过观察分析、阅读理解，并与已知认知结构中的知识进行同化，从而创造性地解决问题，对学生独立思考、加工提取信息及知识迁移和创新的能力要求较高。

3. 关注数学文化，体现德育导向

例10：《九章算术》是我国古代数学的经典著作，书中有一个问题：“今有黄金九枚，白银一十一枚，称之重适等，交易其一，金轻十三两，问金、银各重几何？”意思是：甲袋中装有黄金9枚（每枚黄金重量相同），乙袋中装有白银11枚（每枚黄金重量相同），称重两袋相等，两袋互相交换1枚后，甲袋比乙袋轻了13两（袋子重量忽略不计），问黄金、白银每枚各重多少两？设每枚黄金重x两，每枚白银重y两，根据题意得（ ? ? ）。

评析：本题选自我国古代数学的经典著作《九章算术》，以此弘扬中华数学文化，增强民族自豪感，体现了数学课程育人功能的德育导向。

4. 关注数学理解，考查运用能力

例11：如下图，反比例函数y=（k≠ 0）的图像经过A、B两点，过点A作AC⊥x 轴，垂足为D，过点B作BD⊥x轴，垂足为D，连接AO，连接BO交AC于点E，若OC=CD，四边形BDCE的面积为2，则k的值为_______。

评析：本题背景来源于教材中反比例函数及相似三角形的性质，深入挖掘“反比例函数”的定义，考查学生对参数的准确理解，还要结合相似的相关知识来解题，突出引导学生经历概念形成过程和理解概念本质的重要性。

5. 关注操作实践，助推思维发展

例12：如图，在△ABC中，∠ACB=90°，以点B为圆心，BC的长为半径画弧，交线段AB于点D，以点A为圆心，AD长为半径画弧，交线段AC于点E，连结CD。

（1）若∠A=28°，求∠ACD的度数;

（2）设BC=a，AC=b;

①线段AD的长是方程x2+2ax-b2=0的一个根吗？说明理由。

②若AD=EC，求的值。

评析：本题在设计上以学生熟悉的作图入手，通过实践活动，发现所需要的条件，从而进一步解题。当然本题设计的亮点还在于与勾股定理、一元二次方程等知识点的综合考查。

三、初中数学“好题”的一题多变

数学教育家波利亚认为：“一个有责任心的教师与其穷于应付繁琐的数学内容和过量的题目，不如适当选择某些有意义但又不太复杂的题目去帮助学生发掘题目的各个方面，在指导学生解题过程中，提高他们的才智与推理能力。”基于上述理念，我们认为可以从一道“好题”出发，借题发挥，探索一题多解、一题多变、一题多用的价值，以期培养学生学会从多层次、广视角、全方位地认识、研究问题，培养学生的创新意识和创新能力。

例如：华东师大版初中数学教材九年级上册第2页，问题1：

如图1，用总长为20m的围栏材料，一面靠墙，围成一个矩形花圃，怎样围才能使花圃的面积最大？

改编一：如图2是一个矩形花圃，除墙一面外，原来的三边改成中间再增加两条与AB平行且相等的边;当然还可增加四条边等。

改编二：（2015年·泉州中考24题）：某校在基地参加社会实践活动中，带队教师考问学生：基地计划新建一个矩形的生物园地，一边靠旧墙（墙足够长），另外三边用总长69米的不锈钢栅栏围成，与墙平行的一边留一个宽为3米的出入口，如图所示，如何设计才能使园地的面积最大？下面是两位学生争议的情境：

请根据上面的信息，解决问题：

（1）设AB=x米（x>0），试用含x的代数式表示BC的长;

（2）请你判断谁的说法正确，为什么？

改编三：（2018年·福建中考23题）：如图，在足够大的空地上有一段长为a米的旧墙MN，某人利用旧墙和木栏围成一个矩形菜园ABCD，其中AD≤MN，已知矩形菜园的一边靠墙，另三边一共用了100米木栏。

（1）若a=20，所围成的矩形菜园的面积为450平方米，求所利用旧墙AD的长;

（2）求矩形菜园ABCD面积的最大值。

总之，正如波利亚所说：“好的题目和蘑菇一样，它们都成串生长。”在初中数学教学中，不仅要求教师要具有一双善于發现好题的眼睛，并且面对好题，还要有绝不放过的精神。在平面几何中，三角形的题目可以改编成四边形，平行四边形可以改编成菱形或矩形或正方形等，再结合图形的变换，可让“好题”好上加好。

（作者单位：福建省南安市教师进修学校 ? 362300）

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。