网站首页  词典首页

请输入您要查询的论文：

　

标题 预学在数学新知学习中的实施
范文 林珍






【摘要】新知的获取是一个主动学习的过程，学生应是知识获取的主动参与者。预学新知可以帮助学生在心理上、知识上、思维上做好学好数学的认知，培养其自学的能力，并促使学生喜欢数学，会学数学，会用数学，真正使学生在情感、能力、知识等方面获得全面发展。
【关键词】预学；新知；自学能力
数学是一门科学性和逻辑性较强的学科。在学习数学之初，必须反复了解熟悉它的过程，逐步学会发现它的规律，并在不断发现探索的过程中加深对数学新知的认识。新知的获取是一个主动学习的过程，学生应是知识获取的主动参与者。预学新知可以帮助学生在心理上、知识上、思维上做好学好数学的认知，培养其自学的能力，并促使学生喜欢数学，会学数学，会用数学，真正使学生在情感、能力、知识等方面获得全面发展。
在数学课堂上常碰到类似的现象：学生不了解教师上课的教学意图，没有做好学习新知的准备，教师有备而教，学生无备而学，教师讲得多，学生参与得少，被动接受新知的传授，甚至有学生根本跟不上教师的步骤，学生的主体地位难以体现出来，而且对新知的理解和掌握不够深刻。捷克著名教育家夸美纽斯曾说：“找出一种教育方法，使教师在课堂上少教，学生可以多学。”在“先学后教，以学定教”理念的指导下，我认为在课改实践过程中可以根据学生的实际情况，在课堂教学中增加一个环节，即讲授新知前预学环节。所谓教授新知识前预学环节，是指上课教授新知识前让学生自学本节课的内容，了解本节课的主要内容，便于学生从整体上把握新知识。自学的认识不能仅仅停留在理论层面，更应该结合教学实践进行探索。
一、要重视新课讲授前的预学
著名教育家魏书生曾说过：“学生通过资料能弄懂教材的百分之九十九，教师只起百分之一的作用。”教师要重视学生的新课前预学，不要认为预学使学生提前知道了教学内容，学生就不会慢慢地与教师经历困惑、操作、比较、分析、综合的思维过程。预学是学生自主参与、获取知识的过程，是培养学生自主学习，提高学生自学能力的重要途径。学生只有在开放的学习活动中才能成长，而自学的第一步就是要学会预学。
二、学生在数学预学中需注意的问题
（一）注意预学的内容
预学由两部分组成，即“预”和“学”。“预”就是预习下节课要学习的新内容，在预习的过程中要确定学习目标，预习的内容要全面，不要有遗漏，包括新知探究、理论内容、例题、例题解决步骤、课后练习题等，预习后要有一个大概的印象，并在自己不理解的地方做上标记。“学”就是学习，学习时要有一定的侧重，侧重于对理论知识的理解，将理论知识理解透彻，要注重对例题的学习。书中的例题一般都是很有代表性的题目，要从中发现解题的原则和方法，不要拘泥于答案。
（二）要注意预学的心态
预习完成后，在课堂上一定要注意听教师的讲课，不要认为自己预习了就全会了，没有必要听教师的讲课，其实对知识的了解并不全面，这样的学习态度只会让你学不到知识的精髓。认真听课可以解决预学时不理解的地方或知识点、关键词。
三、教师合理设计预学内容
学生初学预学时，不知从何入手，这时教师要设计好预学任务，让学生带着任务去预学，做到有的放矢，针对性强，最重要的是布置的内容要有层次性，要让学生通过预学、思考，解决三个层次的问题：要让学生预学什么？为什么要让学生预学这些内容？怎么指导学生预学？预学内容要有针对性，把要传授的新知问题化、问题层次化、层次递进化。
首先，揭示学习目标，让学生明确本节课的教学目标，激发学生学习的兴趣，调动学生学习的积极性，使学生能主动地围绕目标进行探究性学习。教学目标要具体，不要抽象；要简明扼要，不宜内容太多；要通俗易懂，让学生一目了然。
例如《余角和补角》中的教学目标：
1.理解余角与补角的概念；
2.能用规范的数学符号语言描述余角、补角，并进行相关的求角问题的计算；
3.理解并掌握余角、补角的性质。
其次，教师根据本班学生的实际情况设计好自学指导的问题。
例如《余角和补角》设计的预学内容如下。
首先设计自学指导（一）。
1.阅读课本第127页的“做一做”，量一量，算一算，∠1+∠2，∠3+∠4的度數分别是多少？
2.阅读课本第128页第一、二、三段，回答：（1）什么叫互为余角和互为补角？（2）定义中的“互为”是什么意思？（3）对角的位置有要求吗？
3.你能用几何语言表示互为余角和互为补角吗？
在解决了余角和补角的定义后，又设计了自学指导（二）。
阅读课本第128页的“动脑筋”：如图1，∠1与∠2互补，∠1与∠3互补，那么∠2与∠3的大小有什么关系？如图2，∠4与∠5互余，∠4与∠6互余，那么∠5与∠6的大小有什么关系？
并回答下列问题：
（1）“动脑筋”中谈到了“等量代换”的概念，你能用自己的话进行描述吗？
（2）补角和余角有什么性质，你能结合图形用几何语言描述吗？
预学要抓住知识的“根”，以教材为根本，让学生学会看书。教师要从组织教学转向组织学生学习，从设计教学转向设计学习，更好地利用预学促进学生自学能力的培养，促进学生对新知的自主建构。
四、预学检测
（一）聚焦问题
教师在学生预学的时间里巡堂检查，在学生预学过程中常常会发现不少学生聚焦相同的问题。这样的问题往往具有共性，教师在新课讲授时必须关注这样的问题，并在课堂上呈现。这样的问题往往很容易激发学生的学习兴趣与热情，是课堂教学中的宝贵资源。
（二）搭建交流质疑的平台，教师适时点拨提升
通过预学设计的问题提问学生，让学生大胆上讲台讲出自己的做法、看法和不理解的方面，让学生之间通过交流互动完成新知的学习。学生讲题的方式更加凸显了学生的主体性，当然教师的主导地位不容忽视，主导在学生讲题中倾听、追问和点评。对于一些个性化的方法和答案，这些方法虽然不具有共性，但非常有新意，有独特的视角与较强的启发性，在课堂中展示这些观点，可以加深学生对知识的理解，提高学习的有效性，对其他学生起到示范作用。还有些方法是错误的，可以把它们作为反例或错例加以应用，让学生能思辨地学习，提升思维深度。在学生讲题的过程中，教师起到的是积极的主导作用，应该进行适时的点拨、引导和组织，要有新的突破和更精彩的生成，完成数学新知的传授。
教师要做到该讲的要讲好，明确讲的内容。讲的内容应该是学生自学后还不能掌握的内容，即自学中暴露出来的主要的疑难问题或练习中的错误。对学生通过自学已经掌握的，坚决不讲。若是后进生做对了，说明全班学生都会了，就不需要教师再讲了。若是后进生做错了，引导中等偏上的学生分析，讲清原因，引导更正、归纳。对极少数学生知识回生的问题，可以个别课外补救。
（三）给予适当的鼓励
对于预学得较好的或者预学有进步的学生，教师可给予适当的鼓励，同样可以激发学生的预学兴趣。还可以让预学得好的学生在班上展示自己的预学作业，并把预学的方法讲给同学们听，让学生不断体验成功，树立自信。
五、新知检测
在新知识生成之后，跳过例题，直接自学检测，这样既可以检测学生在预学过程中对新知、例题的理解程度，也考查了学生对新知的应用。例如《余角和补角》设计的自学检测如下。
讲完余角和补角定义后自学检测（一）。
1.若∠1=40°，则它的余角的度数是_____，补角的度数是______。
2.若∠1与∠2互补，则∠1+∠2=______。
3.若∠1=90°-∠2，则∠1与∠2的关系为___________。
4.判断：
（1）90°的角叫余角，180°的角叫补角。
（2）若∠1+∠2+∠3=90°，则∠1，∠2，∠3互余。
（3）如果一个角有补角，那么这个角一定是钝角。
（4）互补的两个角不可能相等。
（5）互余的两个角一定都是锐角，两个锐角一定互余。
（6）如果∠A=x°，∠B=（90-x）°，则∠A，∠B互余。
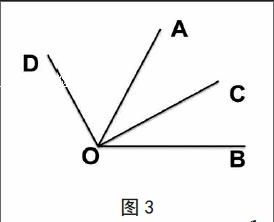
5.如图3，∠BOD=118°，∠COD是直角，OC平分∠AOB，求∠AOB的度数。
6.已知一个角的余角是这个角的补角的，求这个角的度数。
讲完余角和补角性质后自学检测（二）。
（1）若∠1与∠2互余，∠2与∠3互余，则_____=_____，根据是_______________。
（2）若∠3与∠4互补，∠6与∠5互补，且∠3=∠6，则_____=______，根据是______________。
（3）如图4，∠AOC=∠BOC=∠DOE=90°，则图中与∠3互余的角是_________，图中与∠4互余的角是_________，图中有与∠3互补的角吗？_________。
在课堂小结时，教师可引导学生交流：“通过这节课的学习你有什么收获？在学习的过程中，你又有哪些新的疑问？”让学生带着疑问走出课堂，开始新的思考。
实践证明，预学可以使学生由原来的被动学习转变为主动学习，让学生成为学习的主人。教师根据设计的自學指导提出问题，让学生通过预学成为探索者，主动解决问题，并且进行自主合作与探究，最大限度地激发学生的能动性和主体性，有效地促进了学生对数学新知的学习，还培养了学生的自学能力，也给课堂带来了更广阔的空间。
【参考文献】
[1]管敏亚.我的预学我做主[J].教育观察，2014（22）：72-73.
[2]李春光.中学数学课堂有效教学的实践研究[D].南京：南京师范大学，2007.
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2024/12/22 16:54:48