网站首页  词典首页

请输入您要查询的论文：

　

标题 和差角公式及三大定理的统一性
范文 周秋良


大家知道，人教A版普通高中课程标准实验教科书对和差角公式和边角关系三大定理作了精彩的分析，从多个角度引导学生理解掌握。笔者根据教授这一内容的经验认为，教学中还可以引导学生弄清它们之间的统一性。本文给出它们在“托勒密定理”下的统一性证明，供同行参考。
托勒密定理：若ABCD是一个圆O的内接凸四边形，则AB·CD+BC·DA= AC·BD；也就是说，圆的内接凸四边形对边乘积之和等于对角线之积。
一、用托勒密定理推导和差角公式
1.推导两角和的正弦公式
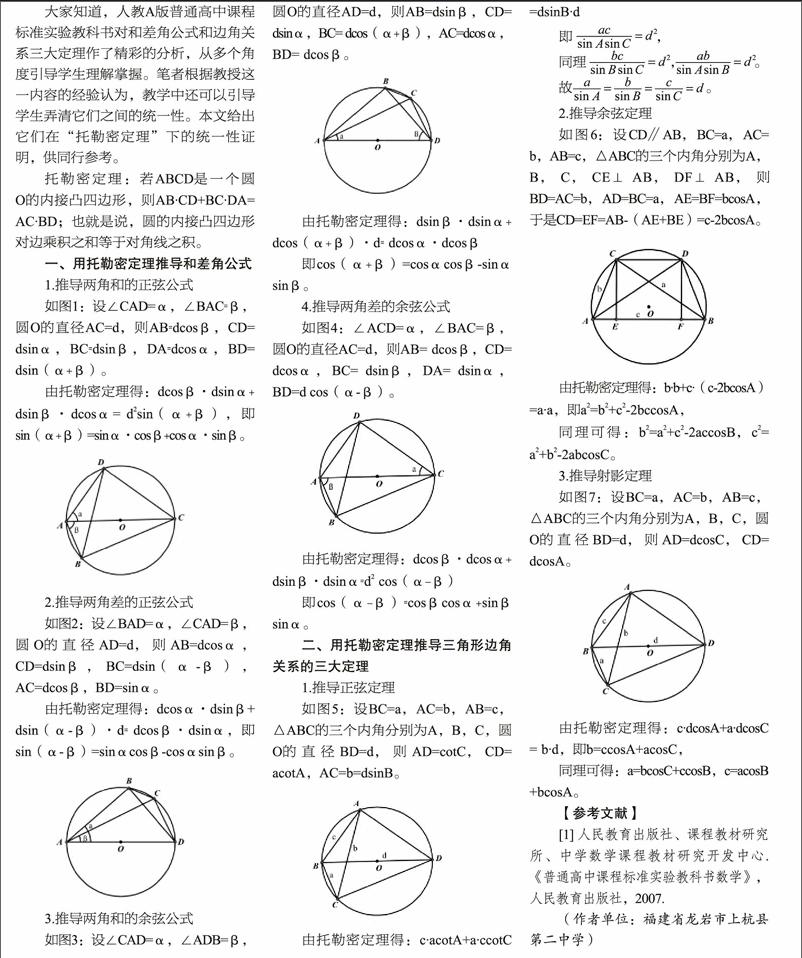
如图1：设∠CAD=α，∠BAC=β，圆O的直径AC=d，则AB=dcosβ，CD= dsinα，BC=dsinβ，DA=dcosα，BD= dsin（α+β）。
由托勒密定理得：dcosβ·dsinα+ dsinβ·dcosα= d2sin（α+β），即sin（α+β）=sinα·cosβ+cosα·sinβ。
2.推导两角差的正弦公式
如图2：设∠BAD=α，∠CAD=β，圆O的直径AD=d，则AB=dcosα，CD=dsinβ，BC=dsin（α-β），AC=dcosβ，BD=sinα。
由托勒密定理得：dcosα·dsinβ+ dsin（α-β）·d= dcosβ·dsinα，即sin（α-β）=sinαcosβ-cosαsinβ。
3.推导两角和的余弦公式
如图3：设∠CAD=α，∠ADB=β，圆O的直径AD=d，则AB=dsinβ，CD= dsinα，BC= dcos（α+β），AC=dcosα，BD= dcosβ。
由托勒密定理得：dsinβ·dsinα+ dcos（α+β）·d= dcosα·dcosβ
即cos（α+β）=cosαcosβ-sinαsinβ。
4.推导两角差的余弦公式
如图4：∠ACD=α，∠BAC=β，圆O的直径AC=d，则AB= dcosβ，CD= dcosα，BC= dsinβ，DA= dsinα，BD=d cos（α-β）。
由托勒密定理得：dcosβ·dcosα+ dsinβ·dsinα=d2 cos（α-β）
即cos（α-β）=cosβcosα+sinβsinα。
二、用托勒密定理推导三角形边角关系的三大定理
1.推导正弦定理
如图5：设BC=a，AC=b，AB=c，△ABC的三个内角分别为A，B，C，圆O的直径BD=d，则AD=cotC，CD= acotA，AC=b=dsinB。
由托勒密定理得：c·acotA+a·ccotC =dsinB·d
即 ，
同理 ， 。
故 。
2.推导余弦定理
如图6：设CD∥AB，BC=a，AC= b，AB=c，△ABC的三个内角分别为A，B，C，CE⊥AB，DF⊥AB，则BD=AC=b，AD=BC=a，AE=BF=bcosA，于是CD=EF=AB-（AE+BE）=c-2bcosA。
由托勒密定理得：b·b+c·（c-2bcosA）=a·a，即a2=b2+c2-2bccosA，
同理可得：b2=a2+c2-2accosB，c2= a2+b2-2abcosC。
3.推导射影定理
如图7：设BC=a，AC=b，AB=c，△ABC的三个内角分别为A，B，C，圆O的直径BD=d，则AD=dcosC，CD= dcosA。
由托勒密定理得：c·dcosA+a·dcosC = b·d，即b=ccosA+acosC，
同理可得：a=bcosC+ccosB，c=acosB +bcosA。
【参考文献】
[1] 人民教育出版社、课程教材研究所、中学数学课程教材研究开发中心.《普通高中课程标准实验教科书数学》，人民教育出版社，2007.
（作者单位：福建省龙岩市上杭县第二中学）
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2025/4/19 0:52:44