
[摘? ?要]首先界定生物模型的概念,然后概述生物模型建构的基本环节:模型准备、模型假设、模型建立、模型检验与修正、模型应用,最后以细菌种群增长曲线的数学模型建构为例,说明生物模型建構的基本过程。
[关键词]模型建构;高中生物;细菌种群增长曲线
[中图分类号]? ? G633.91? ? ? ? [文献标识码]? ? A? ? ? ? [文章编号]? ? 1674-6058(2019)08-0082-03
20世纪30年代,贝塔朗菲倡导用建模方法对生物学进行研究;美国《国家科学教育标准》把“模型”列为科学主题的重点内容之一。在我国,2003年颁布的《普通高中生物课程标准(实验)》(以下简称为《课程标准》)中,首次倡导“假说演绎、建立模型”;2017年新颁布的《课程标准》中,再次明确提出“模型与建构”作为科学思维的重要组成部分,要求在高中生物学必修和选修课程中具体落实。在高中新课程实施过程中,部分学校的教师受传统教学方式的影响,极少让学生自己建构模型,大多是简单地以实物静态模型代替动态的思维模型,这使得学生的创新思维、动手操作能力、合作交流能力、价值观等没有得到有效的培养。因此,在高中生物教学中,教师应积极引导学生建立生物模型,以培养学生的生物学科核心素养。
一、生物模型的概念及分类
1.概念
对于“生物模型”的界定,学术界有多种说法,但其内涵相差不大。笔者认同这样的说法:生物模型是指将生物学研究对象的一些次要的细节、非本质的联系舍去,采用“简化”和“理想化”的方法,对其进行处理,用一种能反映其本质特性的理想物质(过程)或假想结构去描述原型。这种理想物质(过程)或假想结构称之为“生物模型”[1]。
2.分类
生物模型的分类,也有不同的方法,这些分类中有些属于同一大类别中的小类别,其内涵是相同的;有些本质上还是属于同一大类。对此,本文参考了2017年版《课程标准》以及人教版高中生物教科书中生物模型的分类方法,将其分成三大类,即物理模型、概念模型和数学模型。
物理模型。以实物或图画形式直观反映认识对象的形态结构或三维结构,这类实物或图画即物理模型,其包括静态和动态两种结构模型。例如,真核细胞的亚显微结构模型、DNA双螺旋结构模型等属于静态的;植物细胞分裂过程的染色体变化模型则属于动态的。
概念模型。以图示、文字、符号等组成流程图形式对事物的生命活动规律、机理进行描述、阐明,即概念模型[2]。例如,蛋白质合成过程示意图、生物膜系统的特征及功能的描述等。
数学模型。用来表达生命活动规律的计算公式、函数式、曲线图以及由实验数据绘制成的柱状图、饼状图等称为数学模型[2]。例如,典型的种群数量增长型曲线;基因自由组合定律的各种基因型、表现型比例等。
二、生物模型建构的基本过程
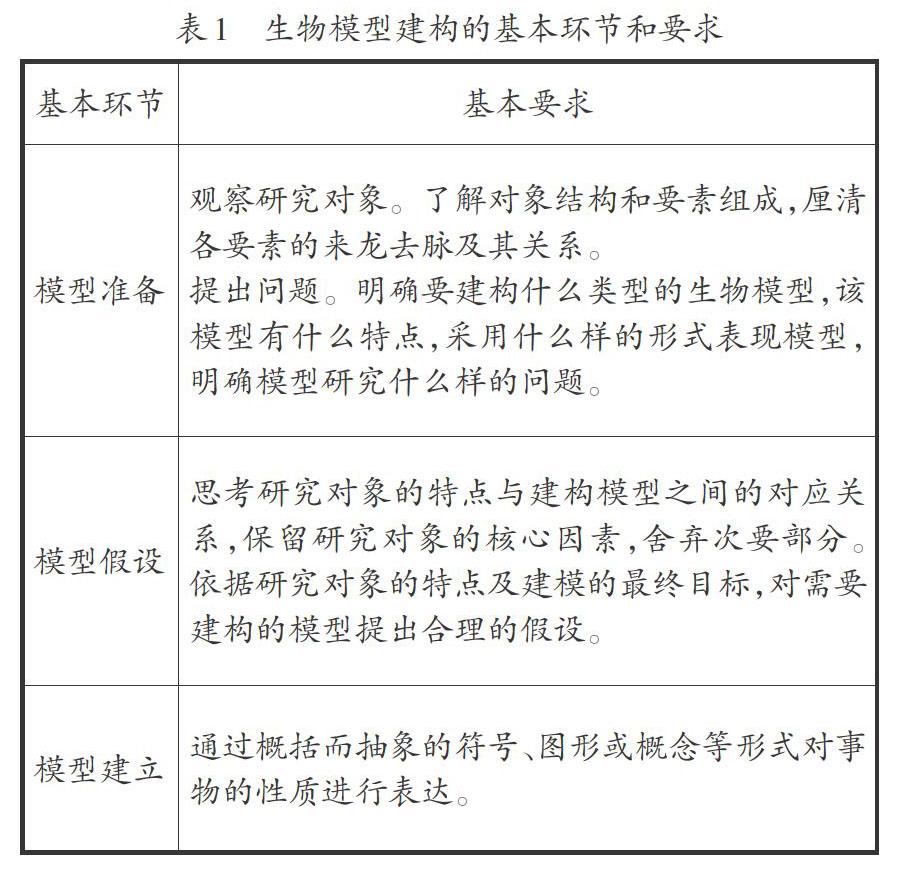
模型建构过程是学生外在行动表达思维的过程,体现了思维和行动的统一。高中生物模型的建构过程,是培养学生科学思维的重要过程。本文参考郝艳翠等教师的文献资料[3],归纳出生物模型建构主要包括模型准备、模型假设、模型建立、模型检验与修正、模型应用等环节。具体如表1。
物理模型、概念模型和数学模型三种模型的建构思路基本相同。本文以细菌种群数量增长曲线为例来说明数学模型建构的具体过程。
1.模型准备
此环节应对“细菌”这一研究对象进行分析。细菌是自然界中分布最广的微生物,它的繁殖方式通常是分裂生殖,在适宜的内外环境条件下可快速繁殖。自然界中的细菌对人类有利也有害,人类利用有益细菌服务生产,减少有害细菌对人类的危害。因此,要以细菌为对象建构模型,则需要了解细菌的形态结构、繁殖方式和速度及细菌种群数量增长与时间、空间的关系等。
2.模型假设
细菌繁殖速度的快慢受多种因素的影响,如食物和空间,环境的温度、空气、pH等理化因素,捕食及其竞争者等生物因素。在研究过程,假如把影响细菌繁殖的所有因素都加以考虑,将使得研究的问题变得复杂,也不易从中找出相应的规律。因此,在研究过程中需建立一种情境假设,在特定的情境下将复杂的问题简单化。例如,若想建立细菌种群数量增长的数学模型,则应假设细菌生活在理想的环境条件下,有充足的食物,足够的空间,适宜的温度、空气和pH值,没有外来的捕食者,等等。影响细菌种群数量的环境因素很多,假设要研究某种单一因素的影响,这种因素则是唯一的变量,如研究氧气的含量对细菌种群数量的影响,则氧气的含量是变量,需设定细菌生活在理想的环境条件下。这样的假设排除其他无关因素的影响,使得研究对象内部受到干扰的因素少,易于揭示细菌种群数量增长的有关规律。
3.模型建立
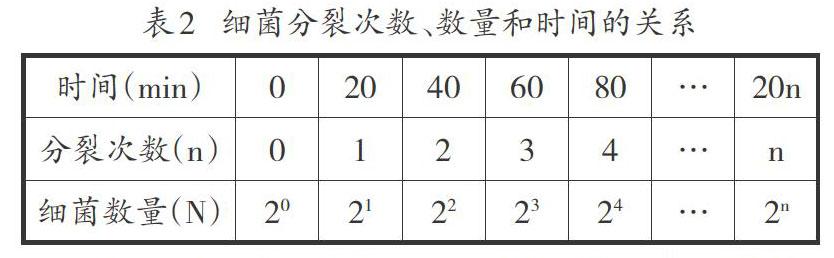
生活在理想的环境条件下的细菌,其通常以分裂方式进行繁殖,20 min就可以繁殖一代。从环境中刚刚存在第一个细菌着手研究,便得出细菌数量与时间的关系,如表2。
由表2可知,假如用N来表示第n代细菌的数量,可以得出:Nn=2n。还可以用曲线图来表示细菌分裂次数、数量和时间的关系,得出细菌数量增长的相应曲线(如图1)。
曲线图呈现出细菌数量处于不断增长的态势,曲线呈“J”型。此时,细菌种群数量增长的数学模型初步建构起来。初步建构的数学模型是否合理?细菌种群数量的实际增长是否和曲线表达的一样?这就需要进一步检验了。
4.模型检验与修正
模型是设定在理想的环境条件下初步建立的,即系统没有外来因素干扰的情况下建成立的。人教版高中生物教材中用一个实例验证该数学模型:1859年,某位英国人把24只野兔带到澳大利亚,100年后,野兔数量增加到6亿只,亿万只野兔和马、牛、羊等动物争夺牧草。由于缺乏食物,大量的野兔啃食树皮,造成植物枯死、环境破坏、水体流失。后来,人们引进了粘液瘤病毒,才逐渐控制了野兔的数量。类似的情况在其他国家也曾出现。
上述模型是假设在环境中刚刚存在第一个细菌的基础上建立的,但种群中起初的细菌数目往往不止一個,可能是很多个,可以用Nn来表示,仍设定在理想的环境条件下建立模型,这就需要对初步建立的数学模型的表现形式进行修正和完善。具体见表3(表3是在表2的基础上修改形成的数据)。
从表3中明显发现,原来的数学式子Nn=2n 变形为Nn=N0 2n,修正了模型的初始数值,曲线形式和走向并没有改变。以N0 =100为例,其细菌种群数量的增长曲线如图2中曲线A所示。
显然,图1曲线和图2中的曲线A,它们的形式和走向并没有改变,同样呈现出“J”型;不同的是,同一时刻,图2中的曲线A代表的细菌数量是图1曲线中细菌数量的10倍。
在生物圈中,生物生存条件是有限的。在一定条件下随着细菌数量的不断繁殖,其种内斗争不断加剧,外在的天敌也不断地对细菌进行捕食,因此,细菌种群的出生率逐渐降低,死亡率逐渐增加。在细菌种群出生率和死亡率相当的情况下,细菌种群的数量维持在一定的范围内,这种状况和细菌种群数量增长的“J”型曲线并不相符。这就要对初步建立的数学模型进行修正,假定图2中的曲线A和曲线B交点之前的时间为细菌种群繁殖的早期,其生活资源充足、空间宽裕,细菌种群数量增长曲线符合“J”型,但随着时间的推移,其增长速率逐渐放缓,较长时间维持在一定的范围内,早期的“J”型增长曲线逐渐演变成整体为“S”型的增长曲线,即曲线B,这就是逻辑斯蒂增长曲线。生态学家高斯的经典实验表明,在一定的空间范围内培养大草履虫,最终得出的大草履虫种群数量增长曲线也呈现“S”型。相对于假设的理想环境条件下细菌种群数量增长建立的数学模型,大草履虫种群生活受到诸如食物、氧气、pH值、空间以及种内斗争等因素的制约,其繁殖速率不可能无限度地增长。以上实例表明,对初步建立的模型进行检验和修正是模型建构中必不可少的环节。
[? ?参? ?考? ?文? ?献? ?]
[1]? 陈建芳.高中生物学“模型教学”尝试[J].中学生物学,2009(4):63-64.
[2]? 肖安庆,李通风.浅谈高中生物建模的教学价值和培养策略[J].中学生物学,2011(7):10-13.
[3]? 郝艳翠.高中生物《稳态与环境》模块生物模型构建研究[D].呼和浩特:内蒙古师范大学,2011.
(责任编辑 黄春香)
- 养猪赚钱方略
- 新式茶饮 搅动市场
- “变脸王”贝因美何去何从?
- 白酒的数字化之路
- 中式点心课堂创新思维培养
- 基于创新创业的食品类专业核心课程改革研究
- 我院烹饪专业学生膳食结构调查及改进建议
- 怎样做好食堂采购
- 创新思维在中职烹饪教学中的应用
- 食品添加剂与食品安全问题的思考
- 食品安全风险分析及其在食品质量管理中的运用
- 食品生产质量安全风险预警指标体系的构建
- 食品安全问题及食品检测发展方向
- 探究微生物检测技术及其在食品安全中的应用
- 食品安全标准在稽查办案中的应用
- 食品质量安全现状与食品质量管理问题思考
- 食品工程质量及食品安全应用
- HACCP原则在食品安全体系中的应用现状
- 我国食品安全现状及对策
- 食品安全快速检测技术研究及应用现状简述
- 食品检测对食品安全的重要性
- 我国食品质量安全现状及全面质量管理对策
- 浙江网络外卖中餐营养分析及食品安全干预措施
- 食品香料对食品的影响和发展趋势研究
- 食品检验技术存在的主要问题及应对策略
- fleecier
- fleeciest
- fleecily
- fleeciness
- fleecinesses
- fleecing
- fleecy
- fleeing
- fleer
- flees
- fleet
- fleeted
- fleeter
- fleetest
- fleeting
- fleetingly
- fleetingness'
- fleetingness
- fleetingnesses'
- fleetingnesses
- fleetingness's
- fleetly
- fleetmanagement
- fleet management
- fleet manager
- 绝无略无
- 绝无的事物
- 绝无间有
- 绝早
- 绝景
- 绝望
- 绝杀
- 绝殊
- 绝气
- 绝水
- 绝活
- 绝流
- 绝渡逢舟
- 绝温郎袂
- 绝漠
- 绝潢断港
- 绝灭
- 绝烟断火
- 绝热发动机
- 绝热过程
- 绝然
- 绝爨断炊
- 绝爱
- 绝版
- 绝版书