《数形结合策略在初中数学教学中的运用》-教育论文，中学教育论文-论文范文参考-科学狗论文网

标题

数形结合策略在初中数学教学中的运用

范文

张春明

数形结合是结合数学实际情况调整数与形的关系，即借助数量、图形将复杂、抽象的数学问题简单化、具体化，进而帮助学生直观地理解问题的实质。数形结合的思想还可以将理论知识具体化，有助于将数学知识应用于实践。数学学科知识的抽象性要求学生具备基本的空间想象力，数形结合的思想有助于学生空间想象力的提高。在初中数学教学中采取数形结合策略有利于拓展学生数学思维，有利于提高教学质量和效率，有利于教学目标的顺利实现。

目前，某些数学教师对数形结合思想持片面认识，完全凭借主观意愿以及多年积累的教学经验来组织教学活动，在一定程度上忽视时代变化以及新课改要求，学生的个体差异、学习基础亦未被考虑在内。再加上教师自身未充分理解数形结合思想的内涵，导致其在实际教学中对数形结合的低效运用，最终为教学工作的开展增加阻力。

虽然新课程改革理念在初中数学教学中持续推进，但数学教师在实际教学中仍习惯于传统的教学模式，学生主体地位没有得到充分体现，长时间处于被动学习状态，这在一定程度上为数形结合思想的运用增加了难度。个别教师应用数形结合思想仅仅是为了应付上级检查，流于形式。之所以会存在这种现象，最大的原因是教师思想守旧，没能从学生的成长出发，认为数形结合会浪费有限的教学时间。随着时间的积累，学生学习数学的能动性会受影响，对教师会产生严重依赖，这对数学教学改革深化、数形结合思想推广有不利影响。

数形结合教学策略在以下几方面的运用，可实现数形结合思想的全过程渗透，对师生教与学能力的提高有促进作用，对初中数学教学现状的改善有重要作用，并能为初中数学教学工作的顺利推进提供支持。

一、应用于概念教学

初中阶段数学概念较多，理解难度相对较大，然而数学概念、公式是后续学习的基础，只有掌握、理解数学概念，才能促进教學工作顺利开展。由于个别概念较抽象，此时运用数形结合思想能够加深学生对概念的印象，并有利于熟记数学概念、理解概念本质。

例如，学习数轴定义时，教师直接画出原点、单位长度、直线方向的数轴，通过数形巧妙结合来补充数学知识，顺利转化数学思想。数形结合不仅运用于数轴概念，而且还能借助数轴解答相关数学问题，如一元一次不等式解集确定、一元一次不等式组求解时，数形结合——数轴的运用会将数形结合思想发挥到极致，数轴有效性再次彰显。今后遇到类似问题时，学生能够自然运用数形结合方法，促进数学问题灵活解答，这对理论知识巩固有重要意义。今后学生学习数学知识能够树立自信心，积极动脑思考、灵活分析，长此以往，有利于学生养成良好的数学学习习惯，掌握有效的解题技巧。在数学概念中运用数形结合策略，能够提高初中生认知水平，通过知识融合提高其数学学习能力。

又如，锐角三角形定义以直角三角形为铺垫，基于单位圆或者直角坐标系定义任意角三角函数，再次得出结论，数形结合两类思想互相影响、互相渗透。间接分析可知，无论是代数问题还是几何问题，都能完成数与形的转化。从另一个角度来讲，数形结合思想能够间接呈现相关数学条件，将内在代数意义与几何意义全面阐述，最终探索途径。

概念教学对其他教学起着引导和奠基作用。如果在概念教学阶段学生重视程度较弱，则意味着学生对数形结合思想运用的能力有待提高。数形结合思想通过结合、转换直观图像与数学语言，通过数学思维调节，最终使数学问题迎刃而解。无论是对教材问题的解答，还是在现实生活中，数形结合思想都具有实用性。下面具体分析数形结合思想在知识教学、习题教学中的运用。

二、应用于具体知识教学

数形结合策略运用于函数中，主要体现在二次函数和三角函数两方面。二次函数这一知识点在考试中占有较大比例，同时也是拉大分值差距的重要内容，此外，二次函数在现实生活问题的求解中发挥重要辅助作用。在初中阶段解答二次函数问题时运用数形结合思想，有利于为高中函数知识的学习奠定基础，有利于锻炼学生的理解能力和分析能力。

例如，教师在数形结合思想引导下建立直角坐标系，引导学生总结函数图像——抛物线的规律和性质，同时有序梳理最值、开口方向等要素间的关系，充分利用已知条件求解，最终使学生意识到数形结合的作用以及现实意义。在三角函数知识的学习中，学生极易混淆三角函数数值，进而在解题过程中出错。对此，教师可运用数形结合教学策略。例如，在学习勾股定理时具体标记三角形各边边长，即数形结合思想的具体体现。

又如，教师讲解例题：学校每月举办一次兴趣问答竞赛，开学后分别举办了以数学、英语、生物为主题的竞赛活动，其中有75人参加了数学竞赛，68人参加了英语竞赛，61人参加了生物竞赛，17人同时参加了数学竞赛和英语竞赛，12人同时参加了数学竞赛和生物竞赛，9人同时参加了英语竞赛和生物竞赛，还有6人共同参与三个竞赛，求参加竞赛的总人数。具体算法如下：

68+75+61-（17+12+9）+6=204-38+6=172

可知总人数共172人。运用数形结合思想，学生能够直观地看到集合，即通过图形化语言获得答案，同时，学生能够理解题目内涵，并在短时间内探索到问题实质，对集合产生新的认知。数形结合思想实用性较强，使学生遇到类似题目时，能够灵活解答。

三、应用于习题教学

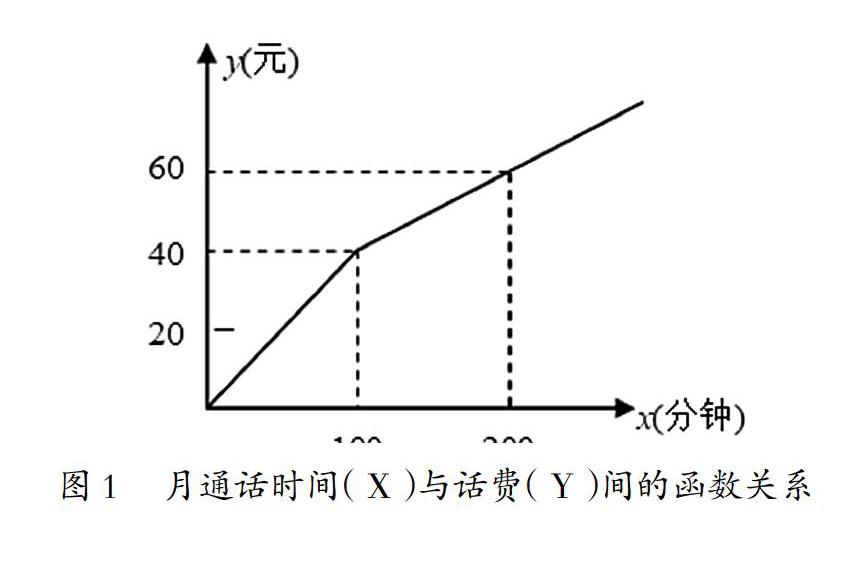
在应用题中渗透数形结合思想，能为对应用题持抵触心理的学生提供解题技巧，提高其数学学习兴趣。例如，某联通公司应用分段计费方式来计算话费，其中，月通话时间（ X ）与话费（ Y ）间的函数关系如图1所示。一次函数以数形结合的方式呈现，使学生能够及时、准确求出当通话时间为100分钟、200分钟时，分别对应的话费是多少。学生通过观察图像，能够总结出函数关系式。当学生认识到了数形结合思想的实用性，再次遇到类似数学问题时，便会主动地运用数形结合思想，有利于提高解决数学问题的综合能力。数形结合思想的运用不仅对学生自我发展有推动作用，也对打造高效课堂，确保数学教学任务及时完成，深化数学改革，优化教学质量起到推动作用。

网络信息时代悄然而至，在这一时代背景中，多媒体信息技术应用于数学课堂，可动态呈现数形结合思想，对学生空间想象力的提高有重要意义。

例如，在进行“平移与旋转”相关教学时，教师为学生展示形式多样的图片，并发挥视频功能优势，动态放映图形变化过程，不仅是对传统呆板教学模式的创新，而且能够吸引学生注意力。此外，多媒体设备在数形结合教学策略中发挥的辅助作用，胜过教师千言万语的总结，使学生的学习印象加深，并对其数形结合意识的培养有重要意义。

又如，学生在学习统计知识时，通过在数据分析的基础上画统计图，使数据在统计图中直观呈现，再结合具体问题进行图表分析，最终选定合理决策。在此过程中，数形结合思想充分体现，符合现阶段数学解题需要，同时也是迎合信息社会发展的表现。因此，学生应掌握统计图制作技巧，并懂得收集、整理有效数据，进而使现实生活中的部分数学问题能够借助统计图有效解决。

综上所述，当前初中数学教学工作正处于转型的关键时期，在实际教学中应用数形结合思想，能够对传统数学教学方法进行补充和创新，能够将复杂的数学问题简单化。数形结合策略在初中数学概念、函数、习题等教学中的应用，最终能够提高数学教学的效率和质量。此外，多媒体设备辅助作用的发挥，有利于营造浓厚的学习氛围，有利于提高学生的数学思维能力。因此，教师在实际教学中应结合具体情况，巧妙运用、大范围推广数形结合思想，以此深化初中数学教学改革，促进学生全面发展。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。