《基于数学核心素养培养的概念教学设计》-教育论文，中学教育论文-论文范文参考-科学狗论文网

标题

基于数学核心素养培养的概念教学设计

范文

钱呈

[摘? ?要]数学核心素养是数学知识、数学能力、数学思想和数学情感态度的综合体现，是在数学学习过程中逐步形成的.概念教学是发展学生数学核心素养的重要载体.

[关键词]核心素养; 概念教学;锐角三角比;意义

[中图分类号]? ? G633.6? ? ? ? [文献标识码]? ? A? ? ? ? [文章编号]? ? 1674-6058（2019）23-0013-03

当前，数学教育的目标已从数学知识的传授转向数学核心素养的养成.数学概念是数学对象本质属性的反映，是构建数学理论体系的基石.在概念教学中，教师常会出现“重知识，轻过程”的现象，将概念看成定论，重灌输轻引导.由于缺乏过程性体验，学生对概念的本质缺乏理解，造成学生思维能力薄弱，所学知识无法灵活迁移，概念教学也缺少了应有的教育价值.数学概念教学的意义不仅在于让学生掌握数学概念本身，更重要的是让学生在获得概念本质属性的过程中，通过观察、比较、分析、归纳、抽象、概括等数学活动，体会蕴含的数学思想方法，优化思维品质，从而促进学生数学核心素养的发展.

现笔者以《锐角三角比的意义》的教学为例，探究如何在概念教学中培养学生的数学核心素养.

一、教学内容

本节课是第一课时，主要让学生经历锐角的正切概念的形成过程，掌握正切、余切的定义.本节内容的学习过程中蕴含丰富的数学思想，有利于培养学生的数学核心素养.在探索发现直角三角形边角关系的过程中，学生经历“感知——猜测——验证——归纳”的问题探究过程，体会从特殊到一般、从抽象到具象的数学思想，丰富学生的数学活动经验.在利用相似三角形论证时，发展学生的推理能力;在引入三角比的符号表示过程中培养学生的符号意识;在锐角三角比的实际应用中，让学生经历实际问题数学化的过程，培养学生的“数学建模”意识.本章的学习为后续高中阶段学习任意角的三角比、三角函数打下基础.

二、教学目标和设计思路

（一）教学目标

1.经历正切概念的形成过程，理解正切和余切的定义，掌握求正切和余切值的方法.

2.经历从实际问题抽象出数学问题的过程，感受数学与生活的联系，体会数学的应用价值.

3.经历“感知——猜测——验证——归纳”的问题探究过程，逐步提高分析问题、解决问题的能力，逐步养成良好的个性思维品质.

（二）教学重点及难点

教学重点：经历锐角的正切概念的形成过程，掌握正切、余切的定义.

教学难点：正切、余切概念的形成.

（三）教学设计思路

三角比的概念来源于实际测量中的应用，教师教学设计时利用航海测量问题引入，体现引入三角比概念的必要性，也激发学生的学习兴趣.探究三角形边角关系时，以“感知——猜测——验证——归纳”为主线，从特殊直角三角形出发，探究边角之间的数量关系，引发学生对一般直角三角形边角关系的猜想，即直角三角形中如果给定一个角的大小，那么它的两条直角边的比值是一个确定的数，引出锐角三角比的概念，从而可知角三角比的定义是合理的.三角比概念的形成过程不仅遵循学生认识事物的规律，还可以帮助学生感知从特殊到一般、从抽象到具象的数学思想方法和思维策略.

三、教学过程

（一）创设情境，引入概念

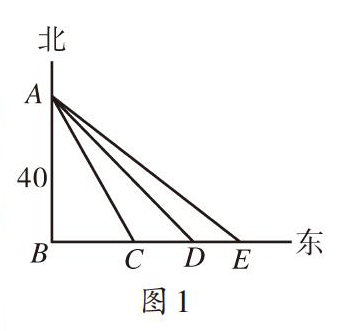
如图1，在港口B的正北方向40千米处有一小岛A，一艘船以每小时25千米的速度从港口B出发沿正东方向行驶.

问题1：48分钟后，船到达C处，问此时船与小岛A相距多少千米？

问题2：船继续向正东方向行驶，到达D处，测得此时小岛A在船的西北方向，问此时船与小岛A相距多少千米？

问题3：船继续向正东方向行驶，到达E处，测得此时小岛A在船的北偏西55°，问此时船与小岛A相距多少千米？

设计意图：一是帮助学生回忆直角三角形的边角性质，巩固直角三角形中的边边关系和角角关系;二是引导学生发现直角三角形的边角之间存在一定的联系，通过设疑引出本节课的研究主题：直角三角形的边角关系.

（二）归纳猜想，感知概念

探究一：特殊直角三角形中的邊角关系

问题1：等腰直角三角形中，45°角的对边和邻边的比值是什么？这个比值是否会随着三角形大小的变化而变化？为什么？

问题2：含30°角的直角三角形中，30°角的对边和邻边的比值是什么？这个比值是否会随着三角形大小的变化而变化？为什么？

图2

设计意图：对特殊情况的观察思考往往能引发对一般规律的探究.从学生熟悉的特殊直角三角形入手探究，将抽象的问题具体化，为后续探究一般直角三角形打下基础.

探究二：一般直角三角形中的边角关系

问题1：探究1中观察到的现象是否存在于一般的直角三角形？当锐角A不是特殊角，而是任意某个确定的角时，对边和邻边的比值是否也确定？如何说明？

如图3，[Rt△ABC与Rt△ADE]中，[∠C=∠AED=90°]，[∠A=α]，那么[BCAC]与[DEAE]有何关系？

问题2：如果锐角A变化，它的对边与邻边的比值是否会变化吗？

如图4，[Rt△ABC]中，[∠C=90°]，[∠BAC>∠DAC]，那么[BCAC]与[CDAC]有何关系？

设计意图：让学生经历猜想、验证、归纳的过程，学生自主探究，合作交流，丰富学生的数学活动经验.学生得出结论后，教师辅以几何画板演示，让学生观察数据的变化，直观感受比值的变化情况，体会“变”与“不变”间的辩证统一，渗透函数思想，为后续学习三角函数做好铺垫.

（三）得出定义，明确概念

通过讨论发现，直角三角形中一个锐角的对边与邻边的长度的比值随着这个锐角的大小的变化而变化，这个比值又随着锐角大小的确定而确定，两者间存在着确定的依赖关系，即[锐角A的对边锐角A的邻边=一个确定的值].

直角三角形中的一个锐角的对边与邻边的比值叫作这个锐角的正切（tangent），锐角A的正切记作tanA，[tanA=锐角A的对边锐角A的邻边=BCAC=ab];直角三角形中的一个锐角的邻边与对边的比值叫作这个锐角的余切（cotangent），锐角A的余切记作cotA.

[cotA=锐角A的邻边锐角A的对边=ACBC=ba].

设计意图：引导学生对概念的初步思考结果进行“抽象化”和“形式化”，运用数学语言（文字语言、图形语言、符号语言）给概念下定义，让概念成为一个稳定的对象.

（四）基础应用，巩固概念

1.如图6， Rt△MNP中，∠N=90°，

（1）∠P的对边是，∠P的邻边是 ;∠M的对边是，∠M的邻边是 .

（2） tanP =，tanM=;cotP=_________，cotM=________.

（3） tanP与cotP有何关系？

（4）? tanP与cotM有何关系？

设计意图：通过练习发现同角的正切与余切之间的关系，互余的两个角的正切与余切之间的关系，通过建立概念间的联系，加深学生对正切和余切概念的理解.

2.如图7，在Rt△ABC中，∠C= 90°，AC=3，BC=2，求tanA、cotA.

设计意图：帮助学生掌握求正切和余切的方法，规范几何书写.

3.在Rt△ABC中，BC=4，AB=5，求 cotA和cotB.

设计意图：进一步明确求正切和余切的条件：（1）必须在直角三角形中;（2）已知直角三角形中的任意两边长，培养学生良好的解题习惯.解决几何问题时，若题目未给出具体图形，养成优先作图习惯;在条件未明确时，注意分类讨论，提高思维能力.

（五）归纳小结，反思提高

问题：通过本节课的学习，谈谈你的收获.

设计意图：教师引导学生归纳小结本节课的知识要点、探究方法、数学思想，使学生对本节课的学习内容有整体、全面的认识，完善学生头脑中的概念体系.

四、教学反思

（一）深入解析概念本质，提升概念教学价值

概念教学的基本目标是让学生理解概念，并能利用概念表达思想和解决问题.要实现这一目标，教师必须深入解析概念.对概念的解析应包含三个方面：一是解析概念的特征，主要包括概念的内涵和外延、概念形成的必要性及合理性、概念不同形式的表征（文字、符号、图形）、概念的地位和作用、与其他概念间的联系等;二是解析概念的教育价值，要揭示概念蕴含的数学思想方法，挖掘在概念形成过程中能够发展的数学能力、数学观念以及数学核心素养;三是解析学生学习概念的认知起点与可能存在的障碍，分析学生的认知基础和教学目标间的潜在差异和距离，确定教学难点及突破难点的方法.

（二）创设有效问题情境，从“激趣”走向“引思”

数学概念是数学抽象的产物，对抽象事物的认识，需要依赖具体事例的支持，在概念教学中创设问题情境具有一定的意义.问题情境的创设要具有典型性和适应性，要能体现概念本质属性的同时，还要符合学生的认知水平，便于学生理解，要有助于学生抽象出共性特征，概括出本质属性，形成数学概念.问题情境的创设要具有目的性和层次性.通过创设有效的情境，帮助学生回顾旧知，建立新概念与原有认知体系间的联系.创设的情境要能体现引入新概念的必要性及实际意义.

（三）以问题驱动思维，让概念自主建构

“APOS理論”中提出概念学习需要经历“操作”“过程”“对象”“图式”四个阶段.“操作”阶段是学生建构数学概念的起点，为概念理解提供数学现实;“过程”阶段是学生通过思考、顿悟将“操作”阶段的感受内化，是对概念的自主建构.教学中需要通过提供大量典型例证，让学生经历属性的分析、比较、综合、归纳、概括活动.有效问题的设计能引领学生充分地参与思考，帮助学生将操作过程中的直观感受抽象概括，逐步获得所需要的概念属性，实现概念内化.问题的设计要具有启发性、探索性和层次性，可以从学生最熟悉的观念出发，让学生在好奇心的驱使下逐步接近概念本质.

[? 参? ?考? ?文? ?献? ]

[1]? 邵光华，章建跃.数学概念的分类、特征及其教学探讨[J] .课程·教材·教法，2009（7）：47-51.

[2]? 石颐园.基于PCK内涵解析视角的初中数学概念教学策略[J].教育理论与实践，2017（8）：51-54 .

[3]? 罗增儒.从数学知识的传授到数学素养的生成[J].中学数学教学参考，2016（19）：2-7.

[4]? 蔡金法，徐斌艳. 也论数学核心素养及其构建[J].全球教育展望，2016（11）：3-12.

（责任编辑黄桂坚）

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。