《高考常考解答题解答技巧例说》-教育论文，中学教育论文-论文范文参考-科学狗论文网

网站首页词典首页

标题

高考常考解答题解答技巧例说

范文

韩宏帅

一、三角函数问题重在“变”——变角、变式与变名

三角函数类解答题是高考的热点，其起点低、位置前，但由于其公式多，性质繁，不少同学对其有种畏惧感.突破此类问题的关键在于“变”——变角、变式与变名.

（1）变角：已知角与特殊角的变换、已知角与目标角的变换、角与其倍角的变换、两角与其和差角的变换以及三角形内角和定理的变换运用.如α=（α+β）-β =（α-β）+β，2α=（α+β）+（α-β），2α=（β+α）-（β-α）.

（2）变式：根据式子的结构特征进行变形，使其更贴近某个公式，方法通常有：“常值代换”“逆用、变形用公式”“通分约分”“分解与组合”“配方与平方”等.

（3）变名：通过变换函数名称达到减少函数种类的目的，方法通常有“切化弦”“升次与降次”等.

其答题的基本思路为：

例1? ? ?（2019年高考浙江卷）? 设函数f（x）=sinx，x∈ R .

（1）已知θ∈[0，2π）函数f（x+θ）是偶函数，求θ的值;

（2）求函数y=[f（x+ π 12 ）]2+[f（x+ π 4 ）]2的值域.

分析：? （1）由函数的解析式结合偶函数的性质即可确定θ的值;

（2）首先整理函数的解析式为y=asin（ωx+φ）+b的形式，然后确定其值域即可.

解：? （1）由题意结合函數的解析式可得：

f（x+θ）=sin（x+θ），

函数为偶函数，所以，对任意实数x都有

sin（x+θ）=sin（-x+θ），

即sinxcosθ+cosxsinθ=-sinxcosθ+cosxsinθ，

故2sinxcosθ=0，∴cosθ=0，

又θ∈[0，2π]，因此θ= π 2 或 3 2 π.

（2）由函数的解析式可得：

y=sin2（x+ π 12 ）+sin2（x+ π 4 ）

= 1-cos（2x+ π 6 ） 2 + 1-cos（2x+ π 2 ） 2

=1- 1 2 [cos（2x+ π 6 ）+cos（2x+ π 2 ）]

=1- 1 2 （? 3? 2 cos2x- 1 2 sin2x-sin2x）

=1- 1 2 （? 3? 2 cos2x- 3 2 sin2x）

=1+? 3? 2 sin（2x- π 6 ）.

据此可得函数值域为：[1-? 3? 2 ，1+? 3? 2 ].

方法点睛：求解此类题的策略：既要注重三角知识的基础性，又要注重三角知识的应用性，突出与代数、几何等知识的综合联系.“明确思维起点，把握变换方向，抓住内在联系，合理选择公式”是三角变换的基本要决.在解题时，要紧紧抓住“变”这一核心，灵活运用公式与性质，仔细审题，快速运算.

二、数列问题重在“归”——化归、归纳

等差数列与等比数列是两个基本数列，是一切数列问题的出发点与归宿.首项与公差（比）称为等差数列（等比数列）的基本量.只要涉及这两个数列的数学问题，我们总希望把条件化归为等差或等比数列的基本量间的关系，从而达到解决问题的目的.这种化归为基本量处理的方法是等差或等比数列特有的方法，对于不是等差或等比的数列，可从简单的个别的情形出发，从中归纳出一般的规律、性质，这种归纳思想便形成了解决一般性数列问题的重要方法：观察、归纳、猜想、证明.由于数列是一种特殊的函数，也可根据题目的特点，将数列问题化归为函数问题来解决.

其答题的基本思路为：

例2? ? ?（2019年高考天津）? 设{an}是等差数列，{bn}是等比数列，公比大于0，已知a1=b1=3，b2=a3，b3=4a2+3.

（1）求{an}和{bn}的通项公式;

（2）设数列{cn}满足cn=? 1， n为奇数，b n 2? n为偶数，? 求a1c1+a2c2+…+a2nc2n（n∈ N *）.

分析：? （1）首先设出等差数列的公差，等比数列的公比，根据题意，列出方程组，求得 d=3q=3 ，进而求得等差数列和等比数列的通项公式;

（2）根据题中所给的cn所满足的条件，将a1c1+a2c2+…+a2nc2n表示出来，之后应用分组求和法，结合等差数列的求和公式，以及错位相减法求和，最后求得结果.

解：? （1）设等差数列{an}的公差为d，等比数列{bn}的公比为q，

依题意，得 3q=3+2d3q2=15+4d ，解得 d=3q=3 ，

故an=3+3（n-1）=3n，bn=3×3n-1=3n，

所以，{an}的通项公式为an=3n，{bn}的通项公式为bn=3n;

（2）a1c1+a2c2+…+a2nc2n

=（a1+a3+a5+…+a2n-1）+（a2b1+a4b2+a6b3+…+a2nbn）

=[n×3+ n（n-1） 2 ×6]+（6×31+12×32+18×33+…+6n×3n）

=3n2+6×（1×31+2×32+…+n×3n），

记Tn=1×31+2×32+…+n×3n ①

则3Tn=1×32+2×33+…+n×3n+1 ②

②-①得，2Tn=-3-32-33-…-3n+n×3n+1=- 3（1-3n） 1-3 +n×3n+1= （2n-1）3n+1+3 2 ，

所以a1c1+a2c2+…+a2nc2n=3n2+6Tn

=3n2+3× （2n-1）3n+1+3 2

= （2n-1）3n+2+6n2+9 2 （n∈ N ）.

方法点睛： “算一算、猜一猜、证一证”是数列中特有的归纳思想，利用这种思想可探索一些一般数列的简单性质.等差数列与等比数列是数列中的两个特殊的基本数列，高考中通常考查的是非等差、等比數列问题，应对的策略就是通过化归思想，将其转化为这两种数列.

三、立体几何问题重在“建”——建模、建系

立体几何解答题的基本模式是论证推理与计算相结合，以某个几何体为依托，分步设问，逐层加深，解决这类题目的原则是建模、建系.建模——将问题转化为平行模型、垂直模型、平面化模型及角度、距离等的计算模型;建系——依托于题中的垂直条件，建立空间直角坐标系，利用空间向量求解.

其答题的基本思路为：

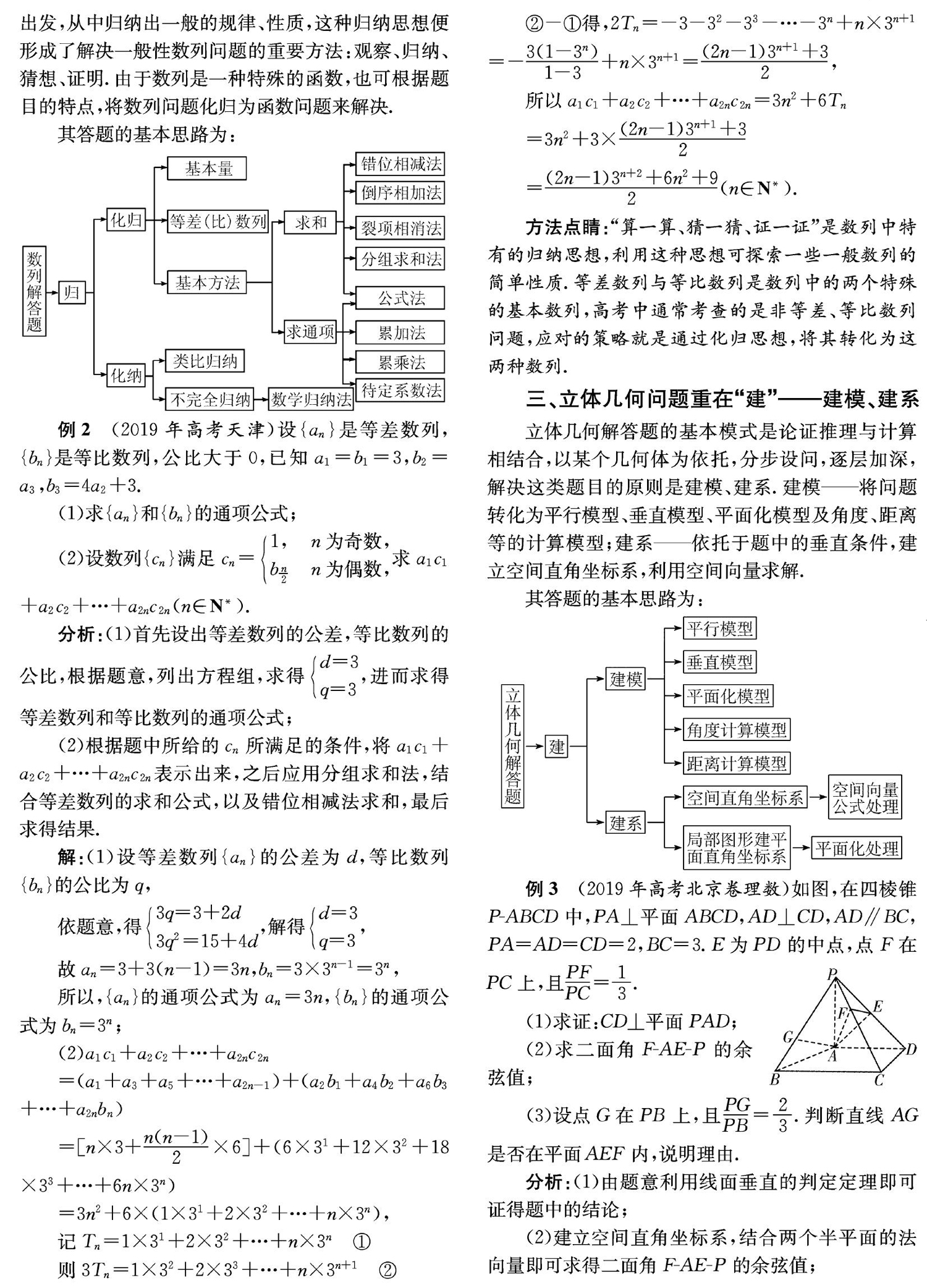
例3? ? ?（2019年高考北京卷理数）? 如图，在四棱锥PABCD中，PA⊥平面ABCD，AD⊥CD，AD∥BC，PA=AD=CD=2，BC=3.E为PD的中点，点F在PC上，且 PF PC = 1 3 .

（1）求证：CD⊥平面PAD;

（2）求二面角FAEP的余弦值;

（3）设点G在PB上，且 PG PB = 2 3 .判断直线AG是否在平面AEF内，说明理由.

分析：? （1）由题意利用线面垂直的判定定理即可证得题中的结论;

（2）建立空间直角坐标系，结合两个半平面的法向量即可求得二面角FAEP的余弦值;

（3）首先求得点G的坐标，然后结合平面AEF的法向量和直线AG的方向向量可判断直线是否在平面内.

解：? （1）由于PA⊥平面ABCD，CD平面ABCD，则PA⊥CD，

由题意可知AD⊥CD，且PA∩AD=A，

由线面垂直的判定定理可得CD⊥平面PAD.

（2）以点A为坐标原点，平面ABCD内与AD垂直的直线为x轴，AD，AP方向为y轴，z轴建立如图所示的空间直角坐标系Axyz，

易知：A（0，0，0），P（0，0，2），C（2，2，0），D（0，2，0），

由PF = 1 3 PC 可得点F的坐标为F（ 2 3 ， 2 3 ， 4 3 ），

由PE = 1 2 PD 可得E（0，1，1），

设平面AEF的法向量为： m =（x，y，z），则

m ·AF? =（x，y，z）·（ 2 3 ， 2 3 ， 4 3 ）

= 2 3 x+ 2 3 y+ 4 3 z=0 m ·AE =（x，y，z）·（0，1，1）=y+z=0 ，

据此可得平面AEF的一个法向量为： m =（1，1，-1），

很明显平面AEP的一个法向量为 n =（1，0，0），

cos< m ， n >=? m · n? | m |×| n | = 1? 3 ×1 =? 3? 3 ，

二面角FAEP的平面角为锐角，故二面角FAEP的余弦值为? 3? 3 .

（3）易知P（0，0，2），B（2，-1，0），由PG = 2 3 PB 可得G（ 4 3 ，- 2 3 ， 2 3 ），则AG =（ 4 3 ，- 2 3 ， 2 3 ），

注意到平面AEF的一个法向量为： m =（1，1，-1），

其 m ·AG =0且点A在平面AEF内，故直线AG在平面AEF内.

方法点睛：立体几何的内容在高考中的考查情况总体上比较稳定，因此，复习备考时往往有“纲”可循，有“题”可依.在平时的学习中，要加强“一题两法（几何法与向量法）”的训练，切勿顾此失彼;要重视识图训练，能正确确定关键点或线的位置，将局部空间问题转化为平面问题;能依托于题中的垂直条件，建立适当的空间直角坐标系，将几何问题化归为代数问题.

四、概率问题重在“辨”——辨析、辨型

概率与统计问题的求解关键是辨别它的概率模型，只要模型一找到，问题便迎刃而解.而概率与统计模型的提取往往需要经过观察、分析、归纳、判断等复杂的辨析思维过程，同时，还需清楚概率模型中等可能事件、互斥事件、对立事件等事件间的关系，注意放回和不放回试验的区别，合理划分复杂事件.

其答题的基本思路为：

例4? ? ?（2019年高考天津）? 设甲、乙两位同学上学期间，每天7：30之前到校的概率均为 2 3 .假定甲、乙两位同学到校情况互不影响，且任一同学每天到校情况相互独立.

（1）用X表示甲同学上学期间的三天中7：30之前到校的天数，求随机变量X的分布列和数学期望;

（2）设M为事件“上学期间的三天中，甲同学在7：30之前到校的天数比乙同学在7：30之前到校的天数恰好多2”，求事件M发生的概率.

分析：? （1）由题意可知分布列为二项分布，结合二项分布的公式求得概率可得分布列，然后利用二项分布的期望公式求解数学期望即可;

（2）由题意结合独立事件概率公式计算可得满足题意的概率值.

解：? （1）因为甲同学上学期间的三天中到校情况相互独立，且每天7：30之前到校的概率均为 2 3 ，

故X～B（3， 2 3 ），从面P（X=k）=Ck3（ 2 3 ）k（ 1 3 ）3-k（k=0，1，2，3）.

所以，随机变量X的分布列为：

X 0 1 2 3

P? 1 27? ?2 9? ?4 9? ?8 27

随机变量X的数学期望E（X）=3× 2 3 =2.

（2）设乙同学上学期间的三天中7：30之前到校的天数为Y，则Y～B（3， 2 3 ）.

且M={X=3，Y=1}∪{X=2，Y=0}.

由题意知事件{X=3，Y=1}与{X=2，Y=0}互斥，

且事件{X=3}与{Y=1}，事件{X=2}与{Y=0}均相互独立，

从而由（1）知：

P（M）=P（{X=3，Y=1}∪{X=2，Y=0}）

=P（X=3，Y=1）+P（X=2，Y=0）

=P（X=3）P（Y=1）+P（X=2）P（Y=0）

= 8 27 × 2 9 + 4 9 × 1 27 = 20 243 .

方法点睛：概率与统计知识的复习应抓住基本概念、基本公式，不需要做难题、偏题、怪题.在审题时，一般按以下程序操作：（1）准确弄清问题所涉及的事件有什么特点，事件之间有什么关系，如互斥、对立、独立等;（2）理清事件以什么形式发生，如同时发生、至少有几个发生、至多有几个发生、恰有几个发生等;（3）明确抽取方式，如放回还是不放回、抽取有无顺序等;（4）准确选择排列组合的方法来计算基本事件发生数和事件总数，或根据概率计算公式和性质来计算事件的概率.

五、解析几何问题重在“设”——设点、设线

解析几何试题知识点多，运算量大，能力要求高，综合性强，在高考试题中大都是以压轴题的面貌出现，是考生“未考先怕”的题型，不是怕解题无思路，而是怕解题过程中繁杂的运算.因此，在遵循“设——列——解”程序化解题的基础上，应突出解析几何“设”的重要性，以克服平时重思路方法、轻运算技巧的顽疾，突破如何避繁就简这一瓶颈.

其答题的基本思路为：

例5? ? ?（2019年高考北京卷理）? 已知抛物线C：x2=-2py经过点（2，-1）.

（1）求抛物线C的方程及其准线方程;

（2）设O为原点，过抛物线C的焦点作斜率不为0的直线l交抛物线C于两点M，N，直线y=-1分别交直线OM，ON于点A和点B.求证：以AB为直径的圆经过y轴上的两个定点.

分析：? （1）由题意结合点的坐标可得抛物线方程，进一步可得准线方程;（2）联立直线方程和抛物线方程，结合韦达定理，表示出A、B的横坐标，设出圆心坐标，利用直径上的圆周角等于90°构造出向量数量积等于0即可证得题中的结论.

解：? （1）由抛物线C：x2=-2py经过点（2，-1），得p=2.

所以抛物线C的方程为x2=-4y，其准线方程为y=1.

（2）抛物线C的焦点为F（0，-1）.

设直线l的方程为y=kx-1（k≠0）.

由 y=kx-1，x2=-4y 得x2+4kx-4=0.

设M（x1，y1），N（x2，y2），则x1x2=-4.

直线OM的方程为y= y1 x1 x.令y=-1，得点A的横坐标xA=- x1 y1 .

同理得点B的横坐标xB=- x2 y2 .

设点D（0，n），则DA =（- x1 y1 ，-1-n），

DB =（- x2 y2 ，-1-n），

DA ·DB = x1x2 y1y2 +（n+1）2

= x1x2 （- x21 4 ）（- x22 4 ） +（n+1）2

= 16 x1x2 +（n+1）2=-4+（n+1）2.

令DA ·DB =0，即-4+（n+1）2=0，則n=1或n=-3.

综上，以AB为直径的圆经过y轴上的定点（0，1）和（0，-3）.

方法点睛：解析几何的试题常要根据题目特征，恰当地设点、设线，以简化运算.常见的设点方法有减元设点、参数设点、直接设点等，常见的设线方法有圆方程的标准式与一般式、直线方程有y=kx+b、x=my+n及两点式、点斜式等形式、还有曲线系方程、参数方程等.

六、函数与导数问题重在“分”——分离、分解

以函数为载体，以导数为工具的综合问题是高考常考的压轴大题，多涉及含参数的函数的单调性、极值或最值的探索与讨论，复杂函数的零点的讨论，不等式中参数范围的讨论，恒成立和能成立问题的讨论等，是近几年高考试题的命题热点.对于此类综合试题，一般先求导，再变形或分解出基本函数，再根据题意处理.

其答题的基本思路为：

例6? ?已知函数f（x）=ex+exlnx.

（1）求曲线y=f（x）在（1，f（1））处的切线方程;

（2）求证：f（x）≥ex2.

（1）? 解析：? f′（x）=ex+e（1+lnx），所以f′（1）=2e，又f（1）=e，所以y=f（x）在（1，f（1））处的切线方程为y-e=2e（x-1），即y=2ex-e.

（2）? 证明：? （法1）f（x）≥ex2ex+exlnx≥ex2ex-1+xlnx-x2≥0，构造函数g（x）=ex-1+xlnx-x2，则g′（x）=ex-1+1+lnx-2x，g″（x）=ex-1+ 1 x -2，g（x）=ex-1- 1 x2 .因为g（x）在（0，+∞）上递增，且g（1）=0，所以当01时，g（x）>0，所以g″（x）在（0，1）上递减，在（1，+∞）上递增，所以g″（x）≥g″（1）=0，于是g′（x）在（0，+∞）上递增，又因为g′（1）=0，所以当01时，g′（x）>0，g（x）递增，所以g（x）≥g（1）=0，命题获证.

（法2）f（x）≥ex2ex+exlnx≥ex2 ex-1 x +lnx-x≥0，构造函数G（x）= ex-1 x +lnx-x，

则G′（x）= ex-1（x-1） x2 + 1 x -1

= ex-1（x-1）+x-x2 x2 = （x-1）（ex-1-x） x2 .

令H（x）=ex-1-x，则H′（x）=ex-1-1，由H′（x）>0可得x>1，由H′（x）<0可得01时，G′（x）>0，所以G（x）在（0，1）上递减，在（1，+∞）上递增，于是G（x）≥G（1）=0，命题获证.

方法点睛：对于不等式ex-1+xlnx-x2≥0，从指对分离的角度来看，可构造出xlnx≥x2-ex-1、lnx≥x- ex-1 x 、 lnx x ≥1- ex-1 x2 、…、 lnx xn ≥ 1 xn-1 - ex-1 xn+1 等一系列式子，由于构造的不等式两端的函数凸性一致，且寻找隔离曲线的难度大，不容易证明.考虑到函数g（x）=ex-1+xlnx-x2的形式不算太复杂，可通过多次求导证明其在x轴的上方（有且仅有一个交点（1，0））.也可以如法2那样将函数进一步改造为G（x）= ex-1 x +lnx-x，法2比法1简单的原因在于G（x）当中的lnx比较“单纯”，求导一次就能消去lnx.函数与导数压轴题计算复杂、综合性强、难度大.可以参变量分离，把复杂函数分离为基本函数;可把题目分解成几个小题; 也可把解题步骤分解为几个小步，注重分步解答，这样，即使解答不完整，也要做到尽可能多拿步骤分.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。