《例谈数学实验在数学教学中的作用》-教育论文，中学教育论文-论文范文参考-科学狗论文网

标题

例谈数学实验在数学教学中的作用

范文

李明刚

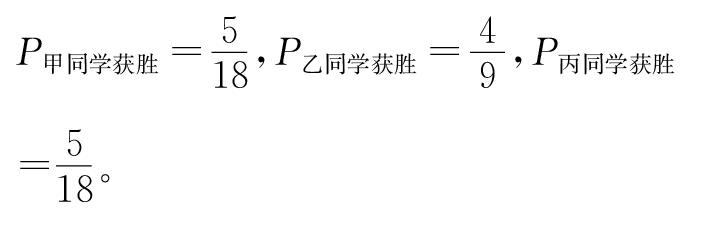
摘要：通过“利用三角板拼角”“游戏是否公平”“探究菱形的性质”“测量旗杆的高度”等教学片段，阐述数学实验的作用：引导学生发现数学规律，帮助学生突破数学难点，培养学生的数学思维，激发学生的数学应用意识。

关键词：数学实验初中数学数学思维

数学实验是数学学习的一种有效方式。在数学教学中，恰当地引入一些数学实验，让学生动手操作，化抽象为直观，化枯燥为有趣，不仅可以激发学生学习的兴趣和热情，调动学生学习的积极性，而且能够引导、帮助学生在探索中发现数学问题、分析数学问题、解决数学问题，发展数学思维;同时，可以培养学生的团队合作精神和人际交往能力。下面，通过几个初中数学教学片段谈谈数学实验的作用。

一、利用数学实验，引导学生发现数学规律

传统的数学教学往往会压缩学习知识的思维过程，造成感知与结论之间的思维断层。在教学适当增加一些数学实验，揭示知识的生成规律，让学生自己去发现数学规律，从而更深刻地理解数学知识。

【片段1】“利用三角板拼角”

师一副三角板有哪些角？

生30°、45°、60°、90°。

师如果用一副三角板拼角，你们能拼出多少个小于平角的角？

生（脱口而出）75°、105°、150°、120°、135°。

师不错。这些角是怎么得到的？

生两两相加就可以得到这些角了。

师还有吗？

（学生迟疑。）

师请你们小组合作动动手，利用一副三角板拼出小于平角的角。请你们拼一个画一个，看看还会不会出现奇迹。

（学生小组实验，约3分钟。）

生可以相减得到15°。

师对了，还有吗？

生（异口同声）不会吧，没有了，相加的都找了，相减的也就一个15°了。

师这样，你们把得到的角按从小到大的顺序排列看看。

生15°、30°、45°、60°、75°、90°、105°、120°、135°、150°。

生好像是15°的递增。是不是还有个165°？我们找找看。

（学生小组实验，约2分钟。）

生老师我们拼出来了，要先画出15°的角，再在15°的基础上画个150°的角，就可以得到165°了。

师很好。

“利用三角板拼角”实验，让学生经历了观察、抽象的模型建立过程，发现了利用三角板可以拼出很多特殊角的数学规律。

二、利用数学实验，帮助学生突破数学难点

数学中的很多结论凭直觉和推理往往都不容易理解，但是通过数学实验获得感性认识，在过程的体验和结果的展示中，难点可以迎刃而解。

【片段2】“游戏是否公平”

（课前，准备若干质地均匀的骰子、乒乓球。）

师下面，我们进行一项游戏，我先来说一说游戏规则：一位同学同时抛掷两枚骰子，若和为2、3、4、5中的一个数，则甲同学获胜;若和為6、7、8中的一个数，则乙同学获胜;若和为9、10、11、12中的一个数，则丙同学获胜。获胜的同学奖励一个乒乓球。（稍停）同学们先猜想一下：甲、乙、丙三位同学，哪位获胜的可能性最大？

生甲。

生丙。

师好像意见不一致嘛！那么，我们验证一下。现在四个同学一组，一位同学抛骰子并当裁判，其余三位同学分别为甲、乙、丙。每位裁判同时抛掷两枚骰子20次，获得乒乓球最多的同学获胜。

（学生小组实验。）

师你们小组谁获胜了？与你们的猜想一样吗？

生不一样，我们小组乙同学获胜。为什么数字少获胜的可能性反而大呢？

师通过多次实验可知乙同学获胜的可能性大。为什么呢？我们通过概率计算来验证一下吧，也解释一下大家的疑惑。

（学生独立计算。）

生P甲同学获胜=518，P乙同学获胜=49，P丙同学获胜=518。

师这个游戏公平吗？

生不公平。

通过抛掷骰子的游戏活动和求随机事件概率的计算过程，让学生解释游戏的公平性。基于感性的实验和回归理性的思考，丰富了学生对概率的认识，强化了学生对相关概率大小的理解。

三、利用数学实验，培养学生的数学思维

数学实验是数学操作和数学思考的结合。通过数学实验，可以激发学生的数学思维，帮助学生认识直观对象的抽象本质。

【片段3】“探究菱形的性质”

（课前，每组准备一张矩形纸片、一把剪刀。）

师你能将一张矩形纸片剪成菱形吗？

（学生说出不少剪的方式。）

师你们能用一刀就剪出来吗？

（学生迟疑。）

师想一想，小组合作，动手操作。

（学生小组实验，约3分钟。）

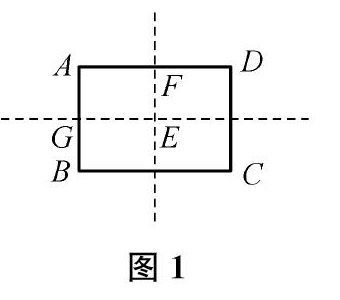
生（出示图1）我们小组先将矩形纸片按虚线对折得到小矩形AGEF，再沿小矩形的对角线GF剪开，将三角形GEF展开就可以得到一个菱形。

师你们怎么知道剪出的图形就是菱形。

生由对折得到这个图形的四边相等，所以是菱形。

师很好！你们能看出你们手中的菱形有什么特征吗？

生是轴对称图形。

生四边相等。

生对角线互相垂直平分。

通过一刀如何剪出菱形，激发了学生折纸的创新思维，由此让学生得到菱形的有关性质，加深了对菱形本质的认识。

四、利用数学实验，激发学生的数学应用意识

数学来源于生活，并应用于生活。数学实验可以进一步引导学生关注生活问题，发现数学的价值，树立数学应用的意识。

【片段4】“测量旗杆的高度”

师我们学校的旗杆大概有多高？

生10米吗？

师我也不知道，这需要你们帮我测量了。

（学生惊讶。）

师请你们想一想：测量旗杆高度有什么方法？

（学生小组讨论。）

生我们小组认为，可以利用影长进行测量。

师说说看，具体的方法是什么？

生找一名同学，测一下他的身高，然后让他站在旗杆附近，可以同时测量他的影长和旗杆的影长，这样就可以求出旗杆的高度了。

师可行吗？

生（齐）可行。

生老师，我们组有不同的方法。

师什么方法？

生我们小组认为，可以利用1米长的杆子帮助测量。只要一名同学通过杆子的顶端观测旗杆顶端，使得自己的眼睛、杆子的顶端、旗杆的顶端在一条直线上，这时记录人与旗杆底部的距离、杆子底部与旗杆底部的距离，并且利用已知的人的高度和杆子的高度进行计算，就可以得到旗杆高度了。

师想法很好。这样测量有没有什么问题？

生老师，不应该是人的高度，而应该是人的眼睛到底面的高度。

师很好！这个小组想到的方法是很好的，就是在细节上要更加严谨。今天，我们就布置这样的作业，就用你们的方法小组合作测影长，看看我们学校的旗杆到底有多高。

测量旗杆的高度是生活实际问题，需要在实践操作的基础上回归理性思考。通过这样的数学实验，不仅可以加深学生对相似三角形、锐角三角函数等数学知识的理解，而且可以提升学生学以致用的意识和能力。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。