《回归数学本真，关注新颖题型》-教育论文，中学教育论文-论文范文参考-科学狗论文网

标题

回归数学本真，关注新颖题型

范文

曾荣渠东剑

摘要：“八省联考”数学卷较好地落实了高考评价体系和数学命题标准的理念，“以新高考Ⅰ卷（山东卷）为基础”，既有所传承，又适度创新，释放出大量信息，值得反复品味。重点比较这两份试卷（适当兼顾这两份试卷与以往江苏卷等的比较），可以发现，试卷结构一致，主体知识板块的考查基本一致，“热点”考查部分一致;情境化（数学文化）试题数量不一致，新题型呈现不完全一致，“冷点”考查不太一致。由此提出的教学建议有：回归数学本真，重视数学阅读，重视开放探究。

关键词：八省联考;新高考Ⅰ卷;数学卷;数学本真

2019年，教育部考试中心研制了《中国高考评价体系》，确立了“一核四层四翼”的整体框架。“一核”是高考的核心功能，即“立德树人、服务选才、引导教学”，回答“为什么考”的问题;“四层”为考查内容，即“核心价值、学科素养、关键能力、必备知识”，回答“考什么”的问题;“四翼”为考查要求，即“基础性、综合性、应用性、创新性”，回答“怎么考”的问题。以此为指南，教育部考试中心结合《普通高中数学课程标准（2017年版）》制订了“高考数学命题标准”，提出了數学学科的“四层”考查内容和具有数学科特点的“四翼”考查要求，来指导新高考全国卷数学学科的命题。

2020年，山东、海南两省率先使用新高考全国卷。2021年，江苏、广东、福建等八省市也将使用新高考全国卷。2021年1月，教育部考试中心组织这八省市的考生进行了一次模拟演练（简称“八省联考”）。本次考试的数学卷较好地落实了高考评价体系和数学命题标准的理念，“以新高考Ⅰ卷（山东卷）为基础”，既有所传承，又适度创新，释放出大量信息，值得反复品味。

一、比较视角下的“八省联考”数学卷特点

虽然本次考试的数学卷与以往的江苏卷等自主命题卷、全国卷以及去年的新高考Ⅰ卷（山东卷）、新高考Ⅱ卷（海南卷）相比，有不少新意，但是考虑到八省市师生未经历过新高考，已然关注两份新高考卷，以及本次考试“以新高考Ⅰ卷（山东卷）为基础”，我们重点比较这两份试卷（适当兼顾这两份试卷与以往江苏卷等的比较），深挖一致性，找出差异性。一致性即蕴含的规律性，有可能是未来高考的趋势，也是我们教学必须明确的方向;差异性有可能是有意释放的信息，部分在以后的高考中实施，提醒我们在教学中注意更新观念，查漏补缺。

（一）一致性

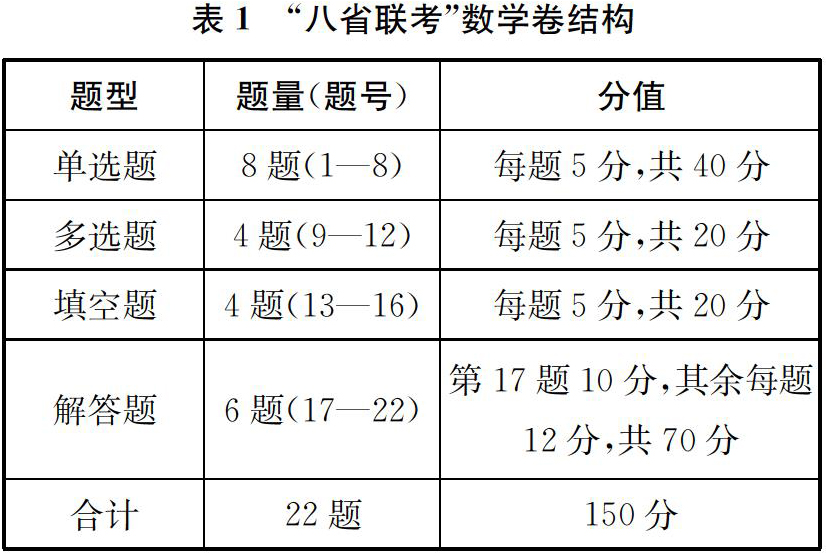
1.试卷结构一致。

试卷沿用了新高考Ⅰ卷的结构（与江苏卷“14填空+6解答”的结构等有较大的差异），各类题型的题量和分值分配如表1所示。经过了2020年新高考和2021年模拟演练的实践，相信这种已被师生认可的试卷结构将会成为2021年新高考数学卷的最终形式。稳定的试卷结构既为教师有效组织复习明确了方向，也为学生合理分配考试时间、科学训练答题技巧提供了依据。

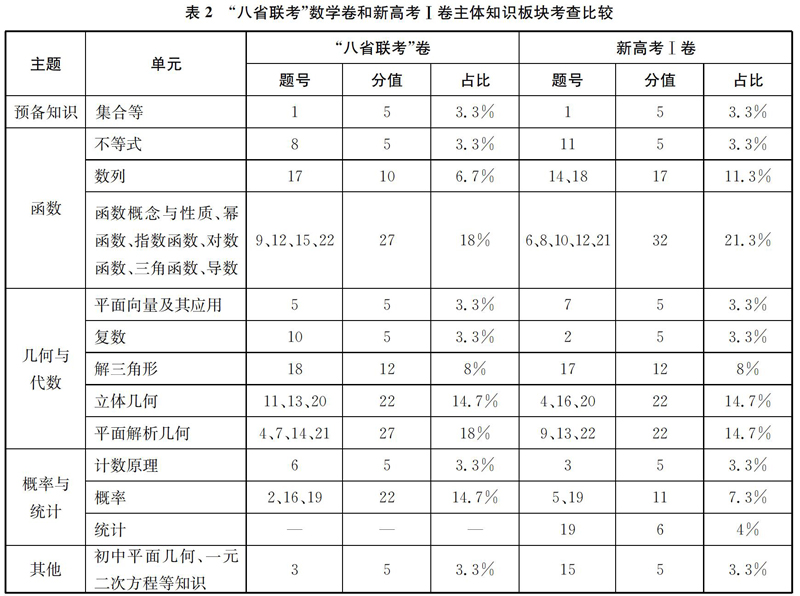
2.主体知识板块的考查基本一致。

试卷和新高考Ⅰ卷在主体知识板块的考查上基本一致（与江苏卷“8个C级考点是重中之重”的传统等有一定的差异），具体如表2所示。需要说明的是，我们统计时，是根据《普通高中数学课程标准（2017年版）》对知识主题及单元进行划分的。试题既兼顾知识覆盖面，又权衡知识板块的学科地位。命题保持这样的一致性，有利于师生整体把握复习方向，让复习有章可循。

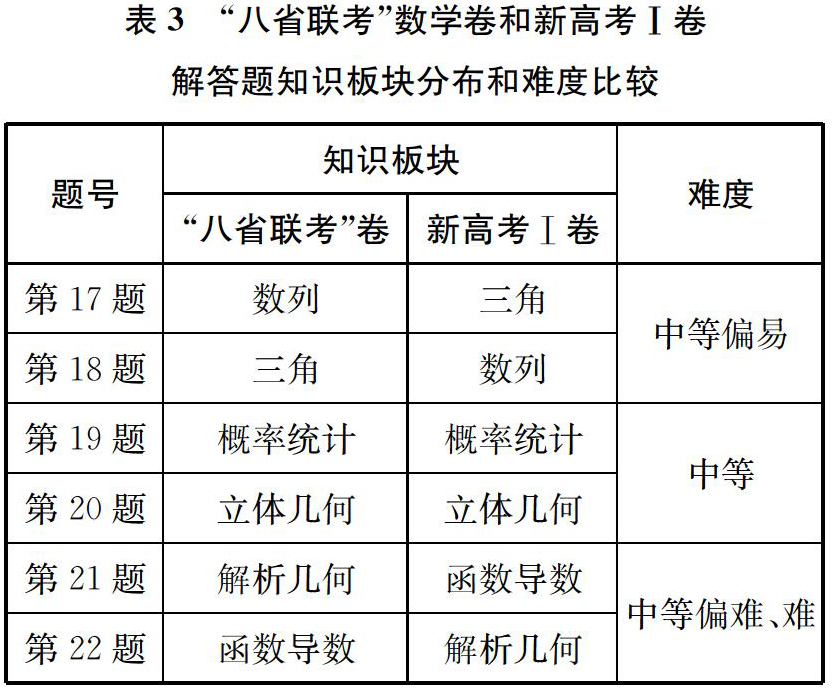
特别值得一提的是，试卷和新高考Ⅰ卷的解答题在知识板块分布和难度上基本一致[与江苏卷“解三角形（三角函数）、立体几何，实际应用、解析几何，数列（不等式）、函数（导数）”的传统等有一定的差异]，遵循了全国卷的命题传统，具体如表3所示。

3.“热点”考查部分一致。

例如，第8题让学生借助“同构函数模型”来比较未知量的大小。这是全国卷近几年的热点题型，虽然其解法具有一定的规律，但是只有深刻理解函数的本质，方能顺利作答。

再如，第22题将指数函数与三角函数相融合，让学生利用导数解决含参数的不等式问题。这是全国卷一贯采用的命题方式，清新自然，不生僻、不做作，但对学生的数学素养提出了很高的要求。

（二）差异性

1.情境化（数学文化）试题数量不一致。

设置真实情境，提出真实问题，可以实现“五育”（德智体美劳）并举、价值引领的目的。本次考试中有这方面的试题，如第16题（物理实验误差控制）、第20题（曲率计算），但与新高考Ⅰ卷相比，占比明显减少。产生的影响是，试卷相比于新高考Ⅰ卷，阅读量明显偏小。由于本次考试带有适应的目的，所以，试卷中融入了很多创新的成分。创新的成分多了，原有的已成熟的、被认可的成分相对就少了。相信，高考卷的情境化试题数量和阅读量最终会找到一个更合适的平衡点。

2.新题型呈现不完全一致。

为落实“四翼”考查要求，高考数学命题有意研发导向积极、灵活新颖、答题方式多样的题型。这有利于考查考生的创新能力，有助于引导师生遵循教学规律，摆脱题海战术。在本次考试和新高考Ⅰ卷中，新高考要求的几类新题型都曾亮相，但各自呈现的类型不完全一致，具体如表4所示。由于本次考试带有适应的目的，所以在最终的高考卷中，命题者有了更多的选择空间。

3.“冷点”考查不太一致。

创新知识载体，强调通性通法，可以引领师生回归数学本真，关注数学思维。相比于新高考Ⅰ卷（乃至其他全国卷），本次考试在知识载体的选择上做了不少创新，以不常见的方式考查了一些相对生僻的知识点。比如，第1题考查集合知识、第10题考查复数知识时，综合性比以往强，难度比以往大;立体几何的小题（第13题）不考查空间向量知识，而考查圆台知识;解析几何的大题（第21题）不考查椭圆知识，而考查双曲线知识;填空题压轴题（第16题）首次考查正态分布知识;概率与统计解答题没考查线性回归方程和独立性检验，而考查独立重复试验的概率与分布列、期望。

此外，个别题目有多种解法，但是，运用核心知识的解法明显比较烦琐，运用非核心知识（甚至补充知识）的解法明显比较简洁。这在某种程度上也可以说是对一些相对生僻知识点的考查。比如，第14题采取联立对角线与圆的方程，求顶点的坐标，再确定边的斜率的思路比较烦琐，而利用直线的方向向量或直线的夹角公式则比较简捷，但后者并非核心知识，甚至超出课标要求。再如，第7题由AB、BC的倾斜角互补，直接利用BC的斜率是定值的课外探究结论解答会很方便。

综上可见，本次考试有点“不按套路出牌”的意思，与“先行一步”的新高考Ⅰ卷相比，又有不少变化。

二、教学建议

新高考命题有规则但无套路，既善于继承，又适度创新。通过考查非“热点”、引入新题型，甚至改变试题排列顺序，打破固有模式，努力破除备考中题海战术的影响。基于这样的命题方式，教师教学要及时改变观念，更新策略。

有必要注意知识点的查漏补缺和补充拓展，但不可加重学生负担;也需要适度的题型训练，但不可套路化。尤其要做好以下几点：

（一）回归数学本真

我们认为，本次考试中的一些“冷点”问题关键不是考知识，而是考思维。因此，要遵循课程标准的要求，回归数学本真，突出核心知识与思想方法，提升学生的数学理解与数学思维，从而以不变应万变。

首先，要帮助学生充分认识知识的来龙去脉（形成过程），建立知识的纵横联系（结构体系）。例如，复习导数概念时，不能只是再现定义，而要再次经历形成过程：定义（过程）—平均变化率—瞬时变化率—函数图像在一点处的切线—函数变化趋势的线性刻画—局部以直代曲……而且，学生通常在宏观层面，对导数与单调性的关系、程式化的利用导数求极（最）值掌握得比较好，而在微观层面，对利用导数研究函数在一个点附近的变化趋势掌握不到位。因此，教师要帮助学生进一步理解导数概念。

高考中，有一类题目常考常新，其一般化描述如下：设定义在R上的函数f（x）（一般含有参数）可导，且f（0）=0，若在x=0附近f（x）≥0恒成立，求f（x）表达式中参数的取值范围。两个函数的大小比较、在更大范围内恒成立等问题都可能转化为这一类问题。比如：

其次，要帮助学生充分感悟知识形成以及问题解决过程中的数学思想方法。以解析几何为例。解析几何研究的是几何对象，利用的是代数方法，就是将几何对象转化为代数对象，利用代数方法研究代数对象，回答所要解决的几何问题。因此，千方百计化归坐标就是解析几何的核心思想方法。在解析几何课程学习中，直线、圆、椭圆、双曲线与抛物线的研究可以说是一个又一个的案例。其中变化的是研究对象，不变的是研究方法。对此，教师要让学生反复经历、充分感悟。例如：

此题有五种常见的解法：（1）证明这两个角的正切值相等，需要用斜率公式将两个角的正切转化为坐标;（2）证明原点O在∠AMB的平分线上，需要用O到角两边的距离相等转化为坐标;（3）证明这两个角的余弦值相等，需要用余弦定理、两点间的距离公式转化为坐标;（4）与平面几何结合，用内角平分线定理的逆定理;（5）与平面几何结合，构造三角形并利用椭圆的第二定义。

显然，方法1是通性通法，其建立的目标函数距离坐标最近，也最簡单，理应是教学中首选的重点方法。方法4、方法5虽然较为简捷，但不是通性通法，一是学生不易想到，二是应用不够广泛。比如，当点M不在该椭圆的右准线上时，方法4、方法5就不能使用，而方法1却可以使用。对这道题的变式探究，可以充分显示通性通法的重要性。

此外，利用这一通性通法也很容易解决如下问题：

（二）重视数学阅读

新高考对学生的数学阅读能力提出了极高的要求（比如本次考试的第20题）。数学阅读能力在一定程度上可以理解为数学核心素养的一种综合体现（“三会”）。只有具有一定的数学阅读理解能力，才能真正感受到数学在实际生活中的重要作用。能否读懂题目、理解题意是解决问题的关键。因此，教学中要特别重视数学阅读能力的培养。

对数学阅读能力的培养不能简单地表现在增加情境题上，关键要落实到日常教学中;也不可能一蹴而就，需要长期的积累。教学中，教师要根据高考的需要、教材的特点、学生的实际整合一些学科性、科学性、生成性资源，编写集知识性、方法性、趣味性于一体的“阅读材料”供学生阅读，并以此创设阅读情境，提炼数学问题，引领本质的揭示、方法的迁移、细节的剖析。

（三）重视开放探究

结论开放题是新高考呈现的重要新题型之一。此类问题有助于加深学生对基础知识的理解，培养学生的发散思维和探究能力。本次考试的第15题就是一道结论开放题：写出一个最小正周期为2的奇函数f（x）=。本题主要考查学生对函数周期性和奇偶性的理解，能否从学过的函数中找到同时满足f（x+2）=f（x）和f（-x）=-f（x）的函数f（x）是关键。其实，各版本高中数学教材中都有此类问题，如人教A版第一册第74页第17题、苏教版第一册第109页第10题等。

*本文系2020年度江苏省社科基金项目“江苏新高考背景下数学学科育人实现机制研究”（编号：20JYB007）的阶段性研究成果。

参考文献：

[1] 于涵.新时代的高考定位与内容改革实施路径[J].中国考试，2019（1）.

[2] 任子朝，赵轩.基于高考评价体系的数学科考试内容改革实施路径[J].中国考试，2019（12）.

[3] 渠东剑.过渡时期的高考数学备考探讨[J].中学数学教学参考，2020（1/2）.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。