《图形与几何教学中数学基本思想的渗透》-教育论文，小学教育论文-论文范文参考-科学狗论文网

标题

图形与几何教学中数学基本思想的渗透

范文

薛生林

图形与几何是小学数学课程四个主要内容之一，数学教材关于“图形的认识”内容的安排体现了从生活到数学、从直观到抽象、从整体到局部的特点。学生在观察操作、整理交流、归纳概括中提出问题，并将问题分为经验型问题、基础型问题和拓展型问题，体会数学知识之间的包含、并列、相关等关系。在问题探究过程中，经历分类、集合、类比的过程，积累提出问题和探究几何知识的经验，逐步感悟数学思想。

一、初探图形特征，渗透分类思想

在图形的认识过程中，学生对所提问题进行分类，在分类的过程中感知不同的问题类型。由于分类过程包含了一系列复杂的思维过程，学生在问题的梳理过程中，发现图形之间的联系和区别，并积累因分类标准不同而分类结果多样的经验。

1.先行感知促提问，初识分类思想

当数学概念多且易混淆时，学生在知识学习前先行学习是非常必要的。学生通过观察学习、操作实践、想象描述等方式激活自己已有的相关知识和经验，在自主探究的过程中生成一个个数学问题。

学生先行学习人教版《数学》四年级上册“角的认识”例2“角的分类”的内容如下。

根据二年级“角的初步认识”的经验，学生提出问题，如角的大小与角的两条边的长短无关，与什么有关？通过预习教材，学生提出问题，如锐角、直角、钝角、平角和周角之间有什么联系和区别？学生通过深度预习教材后，与家长和同学在交流中进一步提出值得研究的问题，如有没有大于180°小于360°的角？有没有比周角大的角？

通过先行学习后，学生提出的数学问题更关注角的不同定义和不同角的特征，以及不同角的联系与区别。这些基础型问题是学生经历知识形成过程的重要载体，是学生几何概念与技能获得的重要途径。在家长和同学等学习共同体的参与下，学生提出的拓展型数学问题是后续进一步学习的内容，是培养学生空间观念的重要载体。

2.突破表象促提问，经历分类过程

学生的几何学习要通过视觉来获得对对象的感知。然而，生活原型的图例会包含与学习无关的特征，如所画直线的有限性、两条直线的不同位置摆放等，这些视觉障碍为学生形成平行与垂直的特征造成障碍。

学生在看到人教版《数学》四年级上册“平行与垂直”时，依据经验第一次提出问题：什么是平行？什么是垂直？画在纸上的两条直线，不是平行就是垂直吗？两条直线的位置关系可以分为平行和垂直吗？学生依据课题望文生“疑”，这些疑问掺杂了学生太多的经验，为学生真正理解这两个概念造成了障碍。

对四年级学生来说，他们开始尝试用更精确的语言来描述平行与垂直的性质，但是，由于概念抽象往往会伴有一定的日常经验。通过整理学生提出的问题，可以看出学生存在视觉障碍。例如，所画的两条直线与方格纸上的平行线重合的两条直线互相平行，那么，斜着画的两条直线怎样判断是互相平行的？从这里可以看出，学生对平行的认识，往往伴有水平放置与竖直放置等生活经验。当然，从学生提出的问题发现，不仅有知觉上的问题，还伴有对分类标准不明的问题，例如，同一个平面内的两条直线，可以分成平行、相交和垂直吗？同一个平面内的两条直线，可以分成平行、重合、垂直吗？这些问题形成学生建立平行与垂直表象时的障碍。根据学生所画的不同图形，让学生按自己的理解进行分类，不同的分类显示着学生对图形特征的表征。

学生经历自主分析、主动探究、分类比较等过程，逐步感知相交分成两直线夹角成90°——互相垂直和两直线夹角成其他角（除90°）——一般相交两类。

二、深探图形性质，渗透集合思想

在图形性质的探究过程中，找出不同图形之间性质的区别和联系，进而提出新的问题，并用集合图的方式表示不同图形之间的关系。

1.比较类推巧提问，感知集合思想

学生空间观念的形成是一个逐步发展的渐进过程。学生在平行四边形和梯形的比较分析中提出问题进而探究平行四边形和梯形的性质之间的关系。学生在操作感知等腰梯形和直角梯形的基础上，在两种梯形的比较以及与平行四边形的比较中提出问题，用集合的方式来建构梯形概念的特征系统。

在学习人教版《数学》四年级上册“平行四边形和梯形”例3“认识梯形的特征”时，学生借鉴探究平行四边形特征的方法自主探究梯形的特征。在探究平行四边形特征时，学生采用直尺和三角尺推的方式探究两组对边分别平行，再采用尺量的方式探究两组对边分别相等。同样，在探究梯形时，学生用直尺和三角尺推的方式探究只有一组对边是平行的。学生在探究的过程中提出问题，如平行四边形有底的描述，梯形的底书上没有描述，那么，什么是梯形的底？上底和下底有什么区别？用量角器量角的大小、用直尺量、用三角尺比直角等方式来感知等腰梯形和直角梯形的特点。学生在操作过程中提出问题，如等腰梯形和直角梯形有什么区别？有没有等腰直角梯形？梯形与平行四边形有什么相同和不同的地方？学生在提问的过程中感知等腰梯形和直角梯形的联系与区别，进一步感知梯形与平行四边形的联系与区别。

2.抽象概括促提问，经历集合过程

按照范希尔提出的几何思维水平的理论，经历过描述分析图形的学生，开始关注图形与图形性质之间的关系，可以提出非形式化的推论。学生通过探究图形的内在属性和其包含关系，分层次将图形进行分类，并用思维导图的方式把这些性质整理展示出来。处于非形式化演绎阶段的学生，通过自主分析、综合比较、抽象概括等方式来表征图形之间的包含关系和并列关系，并用集合的方式对概念进行建构。

在学习“平行四边形和梯形”例4“四边形间的关系”时，学生先回忆已经认识了哪些四边形，再比较各种四边形的特征。学生一般从对边是否平行、是否相等，對角是否相等等方面描述学过的四边形特征。学生在描述过程中生成了一些问题：正方形可以看成特殊的长方形吗？长方形和正方形可以看成特殊的平行四边形吗？四边形除了按对边是否平行进行分类外，可以按对边是否相等进行分类吗？可以按对角是否相等进行分类吗？学生在交流、比较、整理的过程中，用思维导图的方式总结表示出来。从一般四边形出发，逐步增添条件，导出一系列特殊的四边形，从而揭示了各种四边形概念之间的内涵关系（图1）。

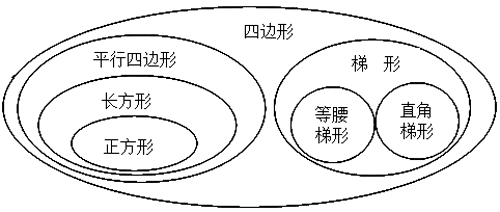
当然，有的学生从对边是否平行来比较各种四边形的特征，用集合图来加以总结展示（图2）。从图2中，我们可以看出各种四边形概念的外延之间的关系，其中有层层包含关系，也有包含中的并列关系。

三、拓展图形知识，渗透类比思想

在图形与几何知识体系中，存在包含、并列等数学关系，学生在观察操作、比较联想中类比，提出含有多种关系的数学问题。

1.关系类比促提问，感悟类比思想

学生通过观察四边形关系的思维导图和集合图，根据不同图形性质之间的关系提出进一步研究的数学问题。学生根据图形之间的包含关系和并列关系，类比提出其他含有包含关系和并列关系的数学问题。当然，学生提出了图形之间的包含和并列关系的数学问题，自然类比提出数学知识之间相交关系的数学问题，甚至提出既有包含关系，又有并列和相交关系的数学问题。

在学习“平行四边形和梯形”例4“四边形间的关系”后，根据集合图，在整理总结的过程中，学生生成了新的问题，如正方形是特殊的长方形，它们之间的关系是包含关系，还有哪些数学知识之间的关系也是包含关系？等腰梯形和直角梯形是特殊的梯形，它们之间的关系是并列关系，还有哪些数学知识之间的关系也是并列关系？这些问题为学生进一步探究数学知识提供了基础。

2.实践类比巧提问，渗透类比思想

研究表明，作图活动是帮助儿童理解形体特征、发展空间观念的一个有效的操作活动。学生通过亲身实践、合作操作等方式探索作图的方法和步骤，在作图练习中形成作图技能，从而培养学生的空间观念。在作图操作、归纳类比等活动过程中不断生成新的数学问题，这些数学问题既是对教材的有益补充，也是后续学习的有力保障。

在学习“平行与垂直”例2“画垂线”时，学生先从已有知识和经验出发，用一副三角板或量角器自主尝试画垂线，再尝试用一把三角尺過直线上一点画垂线和过直线外一点画已知直线的垂线。在实践探究、交流中，学生逐步总结概括画垂线的一般方法和步骤，从而增强作图的规范性。学生在借助点子图练习画两条互相垂直的直线和两条互相平行的直线后，提出了进一步探究的数学问题：在不借助点子图的情境下，怎样画两条互相平行的直线？如何用直尺和三角尺过直线外一点画已知直线的平行线？如何用画平行线的方法来检验两条直线是否平行？学生在探究平行线画法的过程中，进一步感知平行线的判定和两条平行线间的距离处处相等的性质。这些数学问题的探究是学生进一步学习画长方形和正方形的基础，也是学生进一步学习平行四边形和梯形的基础。

[责任编辑：陈国庆]

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。