《触摸知识本质　培养数据分析观念》-教育论文，小学教育论文-论文范文参考-科学狗论文网

标题

触摸知识本质　培养数据分析观念

范文

【摘要】统计知识的习得与数据分析观念的形成已成为当今社会每个公民不可或缺的基本素养。平均数的教学是培养学生数据分析观念的重要载体，它作为一种常用的统计量，其本质是它的代表性，反映了一组数据的整体水平。在教学中，我们应注重激活学生的已有经验，利用可观可感的生活情境，帮助他们触摸平均数的本质，感受平均数的基本特性，进而培养他们的数据分析观念。

【关键词】平均数;整体水平;知识本质;数据分析观念

【中图分类号】G623.5【文献标志码】A【文章编号】1005-6009（2020）01-0071-05

【作者简介】周卫东，南京市长江路小学（南京，210018）校长、党支部书记，高级教师，江苏省数学特级教师，“江苏人民教育家培养工程”培养对象。

【背景】

平均数的学习有三种不同的水平：一是计算水平，重平均数的实际应用——学会求平均数;二是概念水平，重解释平均数的实际意义——知道反映总体水平;三是统计水平，重平均数的深度解释与应用——理解平均数的统计学意义及一些特有属性。我们可以把这三种水平放在“平均数”主题单元教学的框架下思考，正好契合学生深入理解平均数的认知过程。对于平均数的教学，关键是要思考如何在“平均数”的主题下设计认知序列，让学生的学习契合他们的认知规律，从而达成完整、丰满的认知。

美国学习研究专家约翰·D·布兰思福特等人在《人是如何学习的：大脑、心理、经验及学校》一书中指出：“必须用少量主题的深度覆盖去替换学习过程中对所有主题的表面覆盖，这些少量主题使得一些关键概念得到理解。”笔者认为，教师对平均数的教学不能囿于课本，浅尝辄止，而应该让知识的本质活起来，让学生的思维动起来、情感亮起来，从而使学生充分享受数学之于知识世界与人生世界的美好。

本课定位于平均数第三种水平的教学，即统计水平的教学。相较于平均数的第一次认识而言，本课的立意和追求更高些：其一，让学生进一步理解平均数的意义，即表示一组数据的整体水平，在具体的情境中巩固平均数的计算方法;其二，引导学生在鲜活的生活场景中理解平均数的特性，如趋中性、敏感性等，进而培养一定的数据分析观念;其三，激发学生热爱生活、向往真善美的情感，体现学科育人的根本价值。因教学目标不同，此课时课题定为《平均数的再认识》，建议在学生学过教材内容“平均数”之后进行教学。

【教学过程及分析】

一、谈话引入，孕伏概念

课前，教师板书：考得怎么样？

师（出示考试画面）：这是周老师教的四（3）班同学上学期期末考试时的一个镜头。等他们考试结束，我就忙起来了，猜猜看，我在干什么？

生：登记分数，批试卷，分析试卷……

师：都没猜对哦！其实周老师正在跟人聊天呢！你猜，我在跟谁聊天？

生：跟其他老师聊天，跟家长聊天，向领导汇报……

师：的确，我正和我们宋校长QQ聊天呢。想不想看看我们的聊天记录？（出示图1）

美国教育家杜威在《思维与教学》一书中说：“在学校里，学生思维训练失败的最大原因，也许在于不能保障在校外实际生活那样，有可以引起思维的经验和情境。”真实的学习就是要让学生在真实的学习情境中学习解决真实世界问题的方法，在完成真实世界任务的过程中习得知识、获得理解、丰富交往、形成品格。“平均数”诞生于解决实际问题的土壤里，只有真实的生活情境才能让它的意义得以生成与解释。本环节截取了一则学生学习环境中常见的考试场景，巧妙孕伏需要提炼的“平均数”话题，蓄势待发，巧妙自然，“课初始，趣亦生”。

二、逐步逼近，生成概念

师：看了刚刚的聊天记录，你认为四（3）班這次数学考得怎么样？

生：考得还行吧，因为不及格的人很少;有进步，上次那个不及格的同学及格了;还需要进一步努力，毕竟班上还有一个不及格的……

师：在刚刚的交流中，有的说考得还行，有的说有进步，好像还没形成一个相对统一的意见。那么，仅仅靠这三句话，能判断我们班考得怎么样吗？

生：不能，信息太散了。

师：是的！于是宋校长又问——那班级整体水平怎样？（板书：整体水平）

师：宋校长究竟是什么意思呢？

生：想知道全班每个人的分数，想知道全班的总分，想知道班级的平均分……

师：你们同意谁的说法？

生（异口同声）：平均分。

师：是的，表示整体水平的统计量有很多，平均数是最常用的一种。这次四（3）班考试的平均分就是一种平均数。不过，我的试卷统计工作还没进行到这一步，才有了分段统计表。（出示图2）

师：根据这个分段统计表，大胆猜一猜，这次考试的平均分是多少？

生（纷纷猜）：90、93、85、86、89、87……

师：仅凭分段统计表，能知道准确的平均分吗？怎样才能知道准确的平均分呢？

生：把每位同学的分数加起来，除以人数。

师：也就是把所有人的分数先合起来，然后再除，也可以说“先合后分”。（介绍Excel表格后，现场利用Excel表格求出平均分）平均分是多少？（86分）刚刚哪位同学猜得最准？

此环节采取“远镜头渐进”的方式，从三句话切入，让学生在自由评价中感受内容的零散与游离，从而体会到“平均数”产生的必要性，然后根据分段统计表呈现的数据对平均分进行大胆猜测，提升了学生对数据进行科学预测与分析的能力。

三、巧妙对比，理解本质

师：算出了平均数，我们再来看这个页面，这个红色的86是平均数，好好观察，这个表格中还有一个黑色的86，在哪儿？

生：24号同学的考分。

师：想想，这两个86一样吗？

生：不一样，黑86是24号同学自己的分数，红86是全班同学的平均分。

师：谁还有更进一步的补充？

生：这两个86表示的意义也不一样，一个表示个人的，一个表示整体的。

师：是的，相同的两个数，表示的意义不同。那么，有了个人的86，为什么还要全班的86呢？这个红86到底有什么用？

生：个人的分数用来与个人比，表示整体水平的86可以用来与整体比，还可以用来把班上每个学生的成绩与它比较，看看他们在班上所处的位置;如果考卷相同，这个平均分还可以用来与上一届四年级进行比较，看哪一届考得更好。

师：是啊，平均数代表一组数据的整体水平，便于我们进行各方面的比较，解决多种问题。

杜威在《我们怎样思维·经验与教育》一书中指出：“儿童概念的形成，起初并不是从许多现成的事物中抽出一个共同的意义，而是把旧有经验中的结果运用于新的经验中，以便帮助他理解和处理新的问题。”此环节围绕“这两个86一样吗？”這个问题进行深度探问，充分激活学生的已有经验，使其对表示班级整体水平的平均分的作用有了更加准确、生动的理解，为学生全面理解“平均数表示一组数据的整体水平”创造了良好的学习载体。

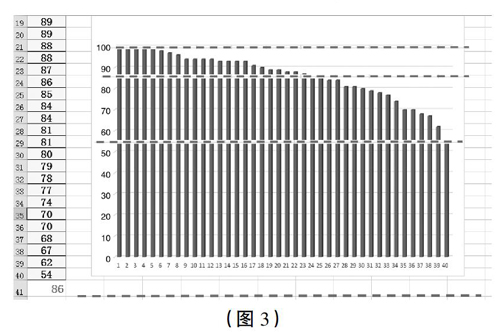
师：同学们，Excel表格还可以把这些分数转化为条形统计图，用直条表示全班的分数情况。（让学生想象后给出统计图，出示图3）

师：这条红色的虚线表示平均分，你觉得把它放在图中什么地方最合适？

生（上台指80到90之间）：因为平均分是86分。

师：是的，在80到90之间。还有不同的想法吗？

生：和24号同学的直条一样高，因为平均分和他的分数一样，都是86分。

师：观察得真仔细，他巧妙地利用24号同学的成绩，精准找到了平均分的位置。

师（指54分处）：如果有同学把这条线放在这儿，你们同意吗？说说你的想法。

生：不合适，这是最低水平。

师（指100分处）：那放这儿是什么水平？

生：最高水平。

师：你们觉得整体水平在怎样的范围内？

生：最高和最低之间。

师：是的，平均数处在最高和最低水平之间的范围内，这是平均数的一个重要特性，在数学上叫作趋中性。

师：同学们，聊到这儿，我想起件事也要向校长报告一下。我们班小范同学生病请假了，没参加考试。站在校长的角度，你会怎么想？

生：小范平常的水平怎么样？小范如果参加考试，对整体水平有什么影响？……

师：很有数据分析意识哦，跟校长的想法差不多。校长是这样说的——他如果参加考试，对整体水平有影响吗？小组讨论后汇报。

生1：有两种可能，考得好的话，整体水平会上升;考得不好的话，整体水平会下降。

生2：还有第三种情况，如果小范的考分和平均分一样的话，就没有影响。

师：同学们想象一下，如果小范考了86.5分，对平均分有影响吗？如果是86.1分，有影响吗？如果是85.9分，有影响吗？

师：尽管只是高了或低了那么一点点，但都会对平均分有影响。正如一位数学家所说——平均数很敏感，一有风吹草动，它就有变化。这是平均数的另一个重要特性，叫敏感性。

充分挖掘数据中蕴藏着的大量信息，驱动学生的思维往宽处走、往深处探，努力彰显数学教学无穷的魅力。本环节中，借助Excel表格的绘图功能，形象直观地呈现全班考试成绩的数据分布。找到平均分所处的位置之后，再与表示最低分与最高分的两根虚线比较，让学生感受到平均数的趋中性;同时，通过对小范考分的多次假设，让学生深刻体悟平均数的敏感性。

四、情境重现，深度思考

师：上学期结束时，小范参加了补考，考了60分。班上有个小孙同学说，小范，如果你考100分，班级总分就能提高40分，正好分给其他40个同学，那班级平均分就提高1分了。对于这样的想法，你们同意吗？

生：他分40分的时候把小范漏掉了，全班一共有41人，要分给41个同学。

师：是呀，多出的40分要平均分给41个同学，没有1分。

师：在我们学校，并不仅仅通过考分来评定一个学生的数学期末成绩，而是通过星级评价来评定。

师（出示图4）：算算平均星级是多少。

师：平均星级8颗星，这个8是怎么来的？

生：把四项的星加起来再除以4得到的。

师：懂你的意思，是先合后分，还有不一样的想法吗？

生：4个数中，有两个8，把最多的10移2给6，就都是8了。

师：把多的移给少的，叫移多补少。求平均数有这样两种基本方法——先合再分和移多补少。

师：小范其实是一个全面发展的同学，在学期结束阶段，他帮学校做了许多事。（呈现三个情境，如下页图5）好好想想，你觉得这三件事中哪些跟我们今天研究的平均数有关？

生1：①和③。

生2：我觉得②也是。

师：①的平均数在哪儿？

生：三次总成绩除以3。

生3：我参加过立定跳远，立定跳远成绩由自己的最高水平决定，所以①与平均数无关。

师：生活经验真丰富，为你点赞！

生：③与平均数有关，在5个评委的分数中还要去掉一个最高分和一个最低分。最高和最低是两个极端数据，对平均数会有影响。

师：再看看②，与平均数有没有关系？

生：有关系，10个班的人数虽然不一定都是一样的，但平均下来大约是40人。

师：是啊！小范用了算式10×40，10表示班级数，40表示各班级的平均人数，他巧妙应用了根据平均数来算总数的原理。

此环节既让学生在巧妙的情境中巩固了“平均数”的两种基本算法（先合后分与移多补少），又让学生在复杂的情境中理解了“参考人数变化了，平均分也要变化”的多维思考。更重要的是，给学生呈现了三则生活场景，使学生对平均数本质的理解跃升到了一个全新的高度。

五、故事结尾，升华价值

师：最后给大家讲一个故事——“埃蒙斯的最后一枪”。埃蒙斯一生中参加过三届奥运会。第一次，2004年雅典奥运会的决赛阶段，他前9枪优势明显，还剩最后一枪。结果站在2号靶位的他把子弹打到了3號靶位，最后得了0环，从而与冠军失之交臂。2008年的北京奥运会，他又来了，前9枪的平均成绩是10.1环，最后一枪却打了4.4环，又一次与冠军错过了。2012年的伦敦奥运会，惊人的巧合，前9枪的平均成绩是10.0环，最后一枪7.6环，再一次功亏一篑。三次奥运，都因为最后一枪的成绩太差而与金牌擦肩而过。听了这个故事？你有什么感想？

生：极端数据容易影响平均数，所以我们要尽可能走好每一步;有时候就差那么一点点细微的东西，就会与重要的事物擦肩而过;关键时刻不能掉链子……

师：感悟得真深刻呀！同学们，当我们都在为埃蒙斯惋惜时，他说，他们笑话我，无所谓，再来过，我知道我人生的唯一责任，就是在活着的时候永远竭尽全力！同学们，我们生活中也有很多考场，也有很多平均数，这其中的道理需要我们日后慢慢体会。

谈到“深度学习”，北京师范大学郭华教授认为：深度学习“深”在哪里？首先“深”在人的心灵里，“深”在人的精神境界上，还“深”在系统结构中，“深”在教学规律中。本环节，通过“埃蒙斯的最后一枪”这一真实故事，让学生不仅从平均数的角度理解极端数据可能给平均数带来的影响，还从生活的角度感悟到“要尽可能走好每一步”“关键时刻不能掉链子”等一些做人做事的朴素道理，叩中了学生的灵魂，激活了学生的情感，真正落实了从“数学教学”走向“数学教育”这一根本性要求。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。