《初中数学几何变换思想的教学策略研究》-理学论文，数学论文-论文范文参考-科学狗论文网

标题

初中数学几何变换思想的教学策略研究

范文

林彩琴

【摘要】數学是一门逻辑性强、抽象性强的综合性学科，注重对学生数学逻辑以及抽象能力的培养.在进行数学教学时，培养学生的数学逻辑、抽象能力以及空间结构想象力非常重要.这一点体现在初中数学几何的教学上，教师是从根本上触发学生的数学思维，激发学生的想象力，培养学生的数学素养.因此，培养学生的数学几何变换思想是初中数学教学工作的重点.但是在实际教学中，教师对数学几何变换思想的变换还存在许多的问题，培养学生的数学几何变换思想效果不佳.本文就初中数学几何变换思想的教学进行讨论和研究，希望能为初中数学几何教学的进步提供一些帮助，更好地促进学生的数学发展.

【关键词】初中数学、几何变换思想、数学素养、教学

一、建构初中数学中的几何教学

（一）初中数学中几何变换思想的概念

初中数学的几何教学是让学生学习三角形、正方形、长方形、多边形等图形的性质、形状、功能，研究它们的空间结构以及实际应用.在此过程中，重视学生的主体探究过程以及学生的建模、变换、转化等思维方法的发展，这对学生的数学思维有重要的作用.

（二）初中数学几何教学的现状

在教学初中数学几何时，部分教师认为只要能懂得一些基本的几何知识，知道一些基本的图形性质和特点就可以了.因此，教师只在教学中强调学生对图形的理解和记忆，没有注重学生对图形的思考及转换，这直接导致了学生的抽象思维能力没有得到应有的锻炼，学生不能从多个方面去思考和发现数学问题，这不利于学生对数学的理解和学习，进而影响了整个数学教学工作的进展，学生的能力得不到加强.同时，这不符合当下新课程标准的改革，不利于学生的全面发展.

（三）变换思想对学生学习几何的重要性

初中数学几何的教学主要是让学生对基本图形有简单的认知和了解，知道图形的性质和结构，为以后高中甚至大学的学习打下基础。同时，数学更是一门具有综合性、抽象性的学科，当教师教学初中数学几何时，学生的思维得到了训练，学生的数学抽象能力得到了提高，学生的发散性思维得到了锻炼.

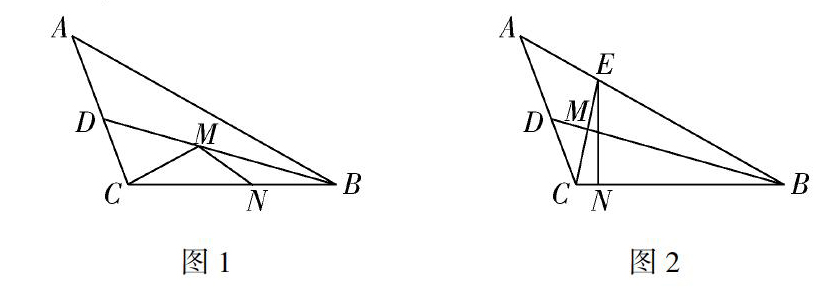
例1问题1，如图1、图2，钝角三角形ABC的面积为20，最长边AB=10，BD平分∠ABC，M、N分别是BD，BC上的动点，求CM+MN的最小值.

分析作点C关于BD的对称点点E，过点E作EN⊥CB于点N，EN就是CM+MN的最小值.

问题2，如图3、图4，三角形ABC为等腰直角三角形，AC=BC=4，∠BCD=15°，点P是CD上的动点，求│PA-PB│的最大值.

分析作点A关于CD的对称点点E，连接CE，EB，并延长EB交CD延长线于点P，EB的长就是

│PA-PB│的最大值.

这两个例题之间可形成“手拉手”的变换方式.

因此，教师将变换思想融入学生的数学教学中能极大地激发学生学习数学的兴趣，提高数学课堂教学质量和学习效率，让学生从本质上学好数学，更加深入地了解和理解数学，让学生能够在数学学习中进行思考，甚至是创新，进而提高学生的自主学习能力，让学生能够从多个角度去思考问题，对学生未来的发展是有极大好处的.

二、在初中数学教学中培养学生几何变换思想的方法和策略

（一）培养学生几何的解题兴趣

初中数学的几何学习是最基础的几何学习，是对平面图形的结构和特点的认知，但这样的学习仍离不开兴趣.如果学生对几何学习有着极大的兴趣，就能够主动学习几何知识，进而研究它的知识结构和特点.例如，如图5，在Rt△ABC中，∠A=90°，AB=AC，点D，E分别在边AB，AC上，AD=AE，连接DC，点M，P，N分别为DE，DC，BC的中点.

1.观察猜想：

图5中，线段PM与PN的数量关系是，位置关系是.

2.探究证明：

把△ADE绕点A逆时针方向旋转到图6的位置，连接MN，BD，CE，判断△PMN的形状，并说明理由.

3.拓展延伸：

把△ADE绕点A在平面内自由旋转，若AD=4、AB=10，则请直接写出△PMN面积的最大值.

教师在解题过程中主要给予学生适当的点拨与启发，关注学生的思考方向，使学生能够利用图形进行合适的变换，激发学生探究几何学习的积极性.因此，在进行几何教学时，教师应该先培养学生的学习兴趣，让学生对几何产生兴趣，这样才能激发学生学习几何的积极性，才能让学生在学习几何的过程中主动参与、积极思考.只有这样，才有利于培养学生的几何变换思想，才能更好地促进教师教学几何.

（二）教会学生正确的解题方法

简单来说，几何数字就是图形的教学.因此，如果要培养学生的几何变换思想，就要让学生对图形有一定的认知和印象。例如，三角形是什么样的？正方形是什么样的？三角形的勾股定理在正方形的哪种情况下能够运用？这些知识的转换需要让学生清楚正方形的特性、三角形的特性、正方形和三角形的关系，即两个三角形可以组成一个正方形，但这样的三角形又得具备什么样的条件呢？

例2已知，如图7①，△ABC中，AB=BC，∠ABC=90°，D为AB的中点，过点B作直线BE与CD垂直，交AC于点E.求证：∠ADE=∠CDB.

分析因为△ABC是等腰直角三角形，所以可将它补成一个正方形ABCF，欲证∠ADE=∠CDB，由于两角没有直接联系，考虑证这两个角都等于某个角，从而使问题得到解决.

证明如图7②，分别过点A、C作AB、BC的垂线，两线相交于点F，延长BE交AF于点G，四边形ABCF是正方形.

∵∠1+∠3=90°，∠2+∠3=90°，∴∠1=∠2.在△ABG和△BCD中，∠1=∠2，AB=BC，∠BAG=∠CBD，∴△ABG≌△BCD∴∠4=∠CDB，AG=BD=AD.在△AGE和△ADE中，AG=AD，∠6=∠5，AE=AE.

∴△AGE≌△ADE.∴∠4=∠ADE，∴∠ADE=∠CDB.

点评对于等腰直角三角形及含有45°角的三角形来说，根据解题的需要，经常可以将原图形补成正方形，以充分运用正方形、直角三角形的性质来解题.

例3定义：按螺旋式分别延长n边形的n条边至一点，若顺次连接这些点所得的图形与原多边形相似，则称它为原图形的螺旋相似图形.

如图8，分别延长多边形A1，A2，…，An的边得A1′，A2′，…，An′，若多边形A1′A2′，…，An′与多边形A1，A2，…，An相似，则多边形A1′，A2′，…，An′就是A1，A2，…，An的螺旋相似图形.

如图9，已知△ABC是等边三角形，作出△ABC的一个螺旋相似图形，简述作法，并给出证明.

如图10，已知矩形ABCD，请探索矩形ABCD是否存在螺旋相似图形，若存在，则求出此时AB与BC的比值;若不存在，则请说明理由.

如图11，△ABC是等腰直角三角形，AC=BC=2，分别延长CA，AB，BC至A′，B′，C′，使△A′B′C′是△ABC的螺旋相似三角形.若AA′=kAC，请直接写出BB′，CC′的长（用含k的代数式表示）.

分析如图9，延长AB到点E，延长BC到点F，延长CA到点D，使得BE=CF=AD，连接EF，DF，DE，△DEF是△ABC的一个螺旋相似图形，证明△DEF是等边三角形即可解决问题.

如图10，假设存在，矩形EFGH是矩形ABCD的螺旋相似图形，设AB=CD=a，BC=AD=b，BE=DG=x，CF=AH=y.分两种情形，利用相似三角形的性质以及相似矩形的性质，构建关系式证明a=b即可解决问题.

如图11，作B′T⊥CB交CB的延长线于点T.设TB=TB′=m，证明△A′CC′≌△A′TB′（ASA），推出A′C=TC′，CC′=TB′=BT，构建关系式证明m=k即可解决问题.

像此类新定义题型，学生只有把握基本的图形概念，了解图形，才能让图形进行转换。同时，只有进行类比运用，才能培养学生的几何变换思想，才能进一步加深学生对几何图形的理解和记忆.

（三）结合模具进行有效教学

几何知识的学习具有很强的空闲性，需要学生具有一定的抽象思维，而多数初中生没有抽象思维的概念，抽象能力比较弱.

教师应该在教学中考虑学生的实际情况，结合模具进行教学，如在研究两点距离最短时，教师可以将数学理论知识和模具相结合，先讲一部分理论知识，再在模具上进行实验，甚至可以让学生自己进行实际验证，这样一来，课堂不再是教师的独角戏，而是让学生参与课堂，充分调动了学生学习的积极性和主动性.

（四）联系实际，运用日常生活策略

数学本来就是从生活中来，回到生活中去.因此，在教学中，教师应该先结合实际生活情况，让学生思考生活中的几何问题，想办法解决问题，再进行指导教学.例如，如图12，正方形ABCD是旅游区域示意图，△ABC部分表示湖面水域.游客在湖岸AB等候乘船，游船从点B出发送游客去湖对岸AC，下船游玩后返回湖对岸AB的上岸点M处，M为AB的中点，游船怎样航行路程最短？如果湖岸AB长为500米，那么游船行驶的最短距离是多少米？

分析作点B关于AC的对称点点D，连接DM.本题是生活中游船的最短航行路径问题，可变换为数学中通过轴对称求线段和的最小值问题.

这样一来，架设起生活与数学的桥梁，把数学知识生活化，让学生体会到生活中时刻存在数学知识，既锻炼了学生的几何变换思维，又锻炼了学生在实际生活中运用数学的能力，这对学生未来的发展和生活有极大的好處.

三、夯实基础，提升素养

初中数学几何是为了给以后更高层次的几何学习打下基础.初中数学几何的教学不是一朝一夕就能完成的，只要我们勤揣摩，就能有效地培养学生的几何变换思想，让学生经历陈述性知识→程序性知识→自动化知识的过程，从本质上理解数学的抽象思维，让学生得到更好的锻炼和发展，提升学生的数学核心素养.

【参考文献】

【1】甘生达.初中数学几何变换思想的教学策略研究[J].新课程（中），2018（8）：26.

【2】刘明.给力的旋转，改变图形位置关系的利器[J].数学教学通讯，2017（11）：77-78.

【3】潘玉.初中数学几何变换思想的教学策略[J].中学生数理化（教与学），2015（8）：96.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。