《浅谈中学数学课堂数形结合思想的渗透》-理学论文，数学论文-论文范文参考-科学狗论文网

标题

浅谈中学数学课堂数形结合思想的渗透

范文

李晋

【摘要】本文主要探討数形结合思想在初中数学课堂中的渗透教学，文章首先阐述数形结合思想对学生能力的提升和未来发展的重要性，随后提出概念、情境和解决不同类型问题具体的课堂教学内容，最后阐述了数形结合思想能够有效地提升学生的空间思维能力，对“数形结合”的渗透教学做出充分的讨论.

【关键词】初中数学;数形结合;策略方案

引?言

“数形结合”是指把抽象的“数”和表象的“形”结合在一起，它是初中数学最常见、最基本的数学思想，对学生的综合素质发展有着明显的帮助，在中学数学教学中具有重要的意义.把数形结合思想贯穿在整个教学过程中，让学生灵活运用数形结合思想解决问题并没有想象中那么容易，存在着许多局限和不足.要想打破“数形结合”教学的局限性，教师应拓宽教学思路，全方位地进行渗透.

一、利用数形结合思想，把握数学概念

通常的数学概念课堂是对现实生活中数学现象的抽象概括，每一个定义前都有长长的修饰词点缀.要想让学生清楚地掌握概念，教师需要指导学生联系实际构建知识网络.由于“数形结合”的概念没有清晰的界定，主要借助学生自身的悟性和理解能力，因此，教师可以选择在任何教学课堂上提及“数形结合”，引领学生把课堂内容与“数形结合”联系在一起.

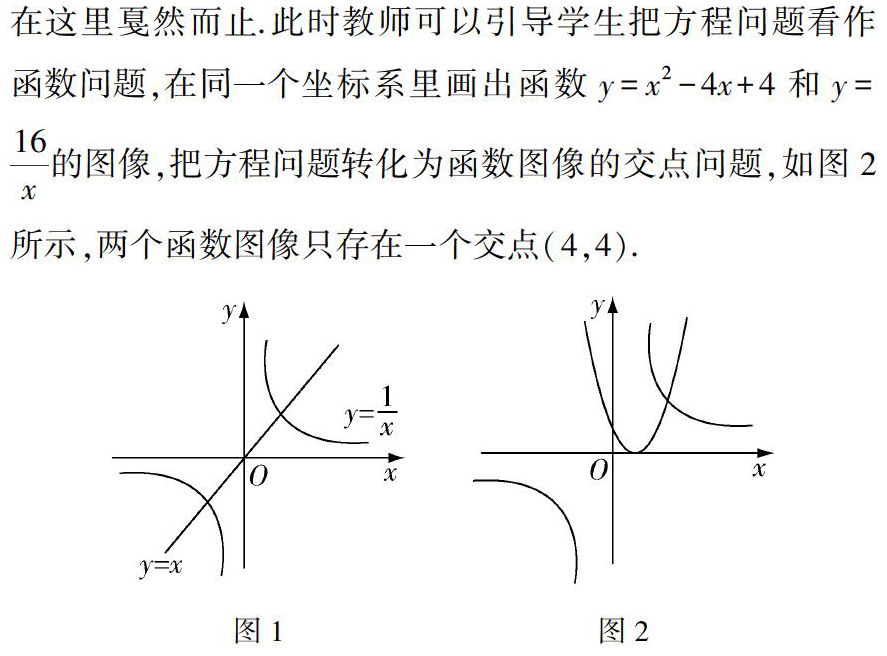
例如，在比较函数y=x和y=1x的函数值大小的课堂上，可供学生选择的方法有很多，一般的思路是把比较函数值大小的问题转化成不等式来求解，其中“数形结合”的办法对学生而言更加直观.如图1所示，由图可以直接得到x=1，x=-1都是两个函数图像交点的横坐标，以此为界即可比较出两个函数值的大小.将“数”与“形”进行结合能够拓展学生的思维，使学生能够巧妙地结合数字和图形解答问题.

一般来说，一次函数在图像上的表达能帮助学生理解解析式的含义，还能给学生提供一种解决问题的新思路.例如，解方程x2-4x+4=16x，根据等式的性质两边同时乘x得到x3-4x2+4x=16，其知识内容超出了教材的范围，解题便在这里戛然而止.此时教师可以引导学生把方程问题看作函数问题，在同一个坐标系里画出函数y=x2-4x+4和y=16x的图像，把方程问题转化为函数图像的交点问题，如图2所示，两个函数图像只存在一个交点（4，4）.

解决函数问题时经常会用到数形结合思想.除此之外，方程、不等式等各种知识内容都能与“数形结合”方法“挂上钩”.这提示教师可以尝试在不同数学教学课堂上联系数形结合思想，于无形中加深学生对“数形结合”的理解.

二、利用“数形结合”情境，引导学生灵活运用

学生对数形结合思想的接触与理解，是“数形结合”在教学中渗透的第一步，第二步则是要让“数形结合”融入学生的学习生活，成为学生的解题方法之一，使学生能够在“图形”和“代数”之间自由地转换.同时，教师要根据具体的问题进行具体分析，这是基本的行为标准.在开展教学时，教师也要根据学生的实际学习情况和认知能力开展针对性的教学，引导学生灵活运用数形结合思想.

以七年级上册“数轴”教学课堂为例，教师可以建设问题场景，引导学生构建直观图像分析、解决问题.例如：在一条马路上竖着一块汽车站牌，在汽车站牌东面3 m，6 m处分别有一棵柳树、一棵杨树，在汽车站牌西面5 m处还有一棵槐树，槐树距离柳树多远？教师把柳树、杨树、槐树以及汽车站牌等生活中的事物放在数学问题中，可以激发学生思考的兴趣.教师还应该指导学生利用数轴图形表示这些事物，让问题变得直观简单，数轴学习的基础知识和能力提升都能在具体的情境和图像表达中显现出来.

无论是讲授新知识还是复习的课堂，使用“数形结合”把代数问题转化为图形问题总能让学生理解起来变得更加简单，数形结合思想在不知不觉中就能被学生接受和使用.

三、利用数形结合思想，巧解具体问题

（一）“数形结合”在几何中的应用

在解决问题的课堂上强调数形结合思想，无疑完美地达到了数形结合思想在课堂中渗透的教学目的.学生面对的几何题目可谓数不胜数，尽管秉承“换汤不换药”的原则，但是做过的题目一旦有了变动，甚至只是数据的改动，就能让学生感到陌生.在解决问题的课堂上强调“数形结合”，一方面有助于学生把“数形结合”日常化，另一方面让学生可以借助直观的图像“吃透”相同类型的题目.

例如，在“过正方形ABCD的四个顶点中的点D任意作一条直线，与直线AB，BC分别交于点E，F，证明点A，C，D在同一个圆上”中，直接通过图形的变化或许能得到结论，但证明过程始终不能正规、具体地描述.倘若教师在平时的教学中强调“数形结合”，学生拥有强烈的意识，就会想到把图形证明问题转化为代数问题，通过计算加以解决.又如，根据题目给出的具体图形和垂直、角度的条件求正切值或余切值时，都可以把图形问题转化为代数问题，使学生在图形与代数的切换中提高解决问题的能力.

利用数形结合思想能够将抽象的知识变得具象，将复杂的知识变得易于理解，进而有效提升学生的学习效率，达到化繁为简的教学目的.同时，数形结合思想为解决实际问题奠定了牢固的基础.在初中阶段，几何问题是教学重点以及难点之一，相对于其他知识内容来说，几何问题较为抽象，如果学生不能快速架构起数学思维，找到准确的切入点，就很难做到快速解题.而在几何问题的解答过程中，如果能够巧妙地利用数形结合思想，将原有的图形数字化，将烦琐的题干信息图像化，就能够将题目直观地呈现出来，大大提升解题效率.

（二）“数形结合”在概率中的应用

在新课程改革中，要求初中数学教师在教学过程中注意加强学生对概率以及统计学知识的学习.在进行统计分析的学习过程中，教师可以通过锻炼学生发现问题、提出问题、解决问题的能力来提升学生的实践能力和探究能力，为学生的未来发展打下牢靠的基础.在概率问题中，利用数形结合思想能够很好地解决问题，如利用树形图进行解题.

例如，在A，B两地之间存在m和n两条路，小明想从A地到达B地，小红想从B地到达A地，现在假设小红和小明两个人出发时间一致，而如果每个人都是从m和n两条路中随机选择一条，请求出两人相遇的概率.

这道题就是最典型的概率问题.如果不利用数形结合思想从图形角度切入进行解题，只是单纯地根据题目进行思考，很难直接得到有效的题干信息，并且学生容易失去耐心，消磨学习兴趣.因此，教师可以引导学生利用数形结合思想来解决概率问题，根据题意画出树形图，题干所给出的信息就能够直观地呈现在学生面前，答案也就呼之欲出了.小红和小明一共可能经过的路径有四种，分别为mm，mn，nn，nm，而其中两人相遇的可能性为两种，即mm，nn，于是可以得出两人相遇的概率为12.

四、利用数形结合思想，培养空间思维能力

所谓空间思维能力，是指对三维空间内的物体的一种思考和理解能力.在初中阶段，学生的数学空间思维能力和创新能力的高低能够在一定程度上反映学生对于数学知识的掌握情况和运用能力.解数学题需要学生能够根据数学中的定义，运用相关的公式、法则等进行综合计算，进而通过题目所给出的条件找到最优的解题方法和运算途径.在初中数学教学过程中，学生的解题能力是由简单转向复杂、由低级转向高级的，而数形结合思想能够有效地培养学生的空间思维能力.同时，学生的空间思维能力能够使学生更好地开展实践，而提升学生的实践能力能够帮助学生更好地掌握数形结合思想，两者相互促进，相互作用.

教师可以通过联系生活实际来开展教学.例如，教师提问：“假设现在有一个长为6 m，宽为5 m，高为2 m的游泳池，现在想要用塑料布将泳池的墙面铺满，那么总共需要多少塑料布？”解此题时，往往会出现学生依据固定的表面积公式来计算的情况，而没有注意到游泳池是没有“盖子”的.在数學的思考方式之中，人们通常将逻辑思维方式作为思维核心.如果初中数学教师在教学过程中对逻辑思维能力过分注重，过于强调，就会导致学生的思维被局限住，学生的求真心理和探索精神就会受挫，进而影响学习.因此，教师要在把握逻辑思维的同时兼顾对学生的想象能力和联想能力的训练.除了逻辑思维以外，数学也需要形象思维以及想象与联想能力，而这两者正是数学的空间思维能力的重要组成部分，也是培养学生数形结合思想的重要方法.

结?语

总之，数形结合思想的全方位渗透能让学生简明扼要地理解数学概念，在数学情境中充分消化知识内容，使得分析解决问题的思维更加广阔灵活，这是学生的进步，也是教学的成功.

【参考文献】

[1]蔡啸.数形结合思想在初中数学教学中的实践研究[D].哈尔滨：哈尔滨师范大学，2016.

[2]刘文斌.浅谈数形结合思想在初中数学教学中的渗透[J].吉林教育，2017，（01）：56.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。