《测量模态不确定的梁式结构随机有限元模型修正》-工学论文，振动工程论文-论文范文参考-科学狗论文网

标题

测量模态不确定的梁式结构随机有限元模型修正

范文

陈辉张衡李烨君

摘要：针对测量模态不确定导致的结构修正参数随机的实际情况，提出了一个随机模型修正方法。该方法以随机有限元法为基础，将结构修正参数表示为多变量非正交多项式展开式，建立了表达随机响应和待修正参数之间精确关系的随机模型修正方程。采用混合摄动-伽辽金方法对该方程进行求解，得到了修正参数的统计特征。数值算例表明，采用测量的前三阶竖向位移模态信息对结构参数进行修正，所提方法的修正结果与蒙特卡洛方法模拟结果一致，但耗时较少。采用修正参数计算得到的随机响应和测量结果吻合很好，验证了本文方法的有效性。

关键词：模型修正; 随机结构; 测量模态; 高阶摄动-伽辽金; 随机有限元

中图分类号： TU317+.1; TU311.3 ?文献标志码： A ?文章编号： 1004-4523（2019）04-0653-07

DOI：10.16385/j.cnki.issn.1004-4523.2019.04.012

引言

在建筑结构中，要准确地进行结构动力学分析，首先必须建立结构动力学模型。目前普遍采用的是有限元法。如果有限元模型是正确的，那么一般认为预测的结果会比测量结果更为准确。因为大多数情况下人们不会怀疑通用的数值分析结果例如有限元计算结果的正确性。另一方面，随着现代测量仪器的测量精度越来越高，如果测量结果与真实结果出现误差，一般认为建模是有问题或不准确的（如没有正确考虑结构参数的选取，边界条件不符合实际等），因此需要借助测量结果来修正建立的有限元模型[1]。然而，受环境（温度、湿度、振动）、测量软件、测试人员经验的影响，测量结果具有不确定性或随机性，而不确定性或随机性的测量结果必然会导致修正结构模型出现不确定性或随机性，因此开展随机模型修正具有重要意义[2]。根据结构随机测量数据来反演不确定性结构参数的过程称为随机模型修正。通常的随机模型修正方法是让测量统计值和预测统计值之间的误差最小化来实现。国内不少学者已经从不同角度采用多种方法对其展开了研究和探索。1998年，美国加州理工的J L Beck教授及其合作者考虑到前述确定性模型修正中存在的问题，开始将贝叶斯方法应用到线弹性土木结构的随机模型修正中来[3-4]。该方法最大的特点是采用随机抽样的方式抽取待修正参数的样本，通过比较所抽取样本对应的响应是否与测量结果一致来得到修正参数。这样可以避免逆向求解时的方程病态问题。但是抽样过程中重复计算结构响应会非常耗时，这对于大型结构是不可接受的。同时当修正参数太多时，传统的吉布斯（Gibbs）抽样方法或MH（Metropolis-Hasyings）抽样方法限制了该方法的使用。近年來，Ren建立了结构响应（频率）和修正参数之间关系的高斯替代模型，并在贝叶斯方法中引入了高效的DRAM抽样方法对一座人行天桥进行了修正[5]。另外，摄动法因为可以很好地衔接确定性有限元而受到了广泛的关注和研究[6-7]。该方法中运用一阶泰勒展开的随机有限元法居多。当测量数据的不确定性较小或输入输出关系为线性时，摄动法可以获得令人满意的修正结果。但当输入输出为非线性关系时，只用输出（修正参数）随机量的1，2阶矩来做模型修正就会丢失高阶矩信息，必然会产生修正误差，当非线性程度较高且输入随机量（测量数据）的变异性较大时，这种误差会更大。同时，现有的摄动法大多数都是通过迭代优化来修正参数的，没有建立从概率上描述输入输出关系的精确模型。考虑到确定性有限元模型修正的自然推广，本文采用随机有限元方法进行有限元模型修正[8]，并采用混合摄动-伽辽金法及正则化技术对修正方程进行求解[9]。

在实际测量中不可避免地存在测量误差，假定频率测量误差服从均值为零，变异系数为0.02的β分布，这是一种实际测量中测量变异性较大的情况。

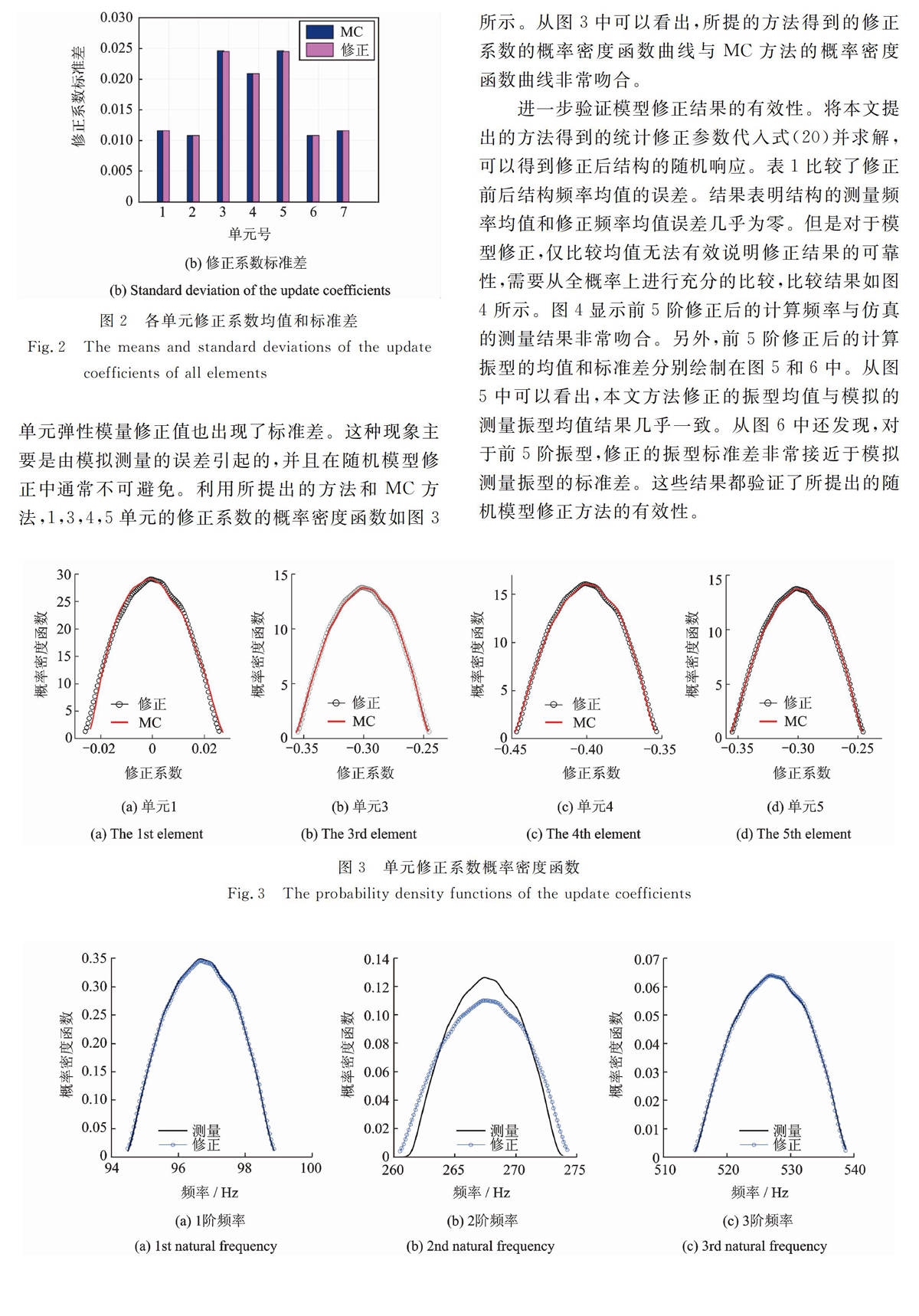
同时假定振型各节点误差服从均值为零，变异系数为0.02的β分布。选定所有单元的刚度作为修正对象。实际模态测试中，测量信息往往有限，同时高阶模态测量误差较大。结合工程实际，选取低阶测量模态（前3阶）作为有效的测量信息，各阶完整模态用测量的竖向位移模态扩阶得到[15-16]。用所提出的方法对固支梁进行模型修正。同时进行十万次的蒙特卡洛模拟（MC）得到统计修正结果，用于与本文方法进行对比。计算得到各单元修正系数的均值和标准差如图2所示。

从图2中可以看出，本文方法得到的统计修正结果和十万次的蒙特卡洛模拟得到的结果基本一致，验证了该方法的准确性和有效性。值得一提的是，本文所提出的方法仅用了不到十次的有限元模型计算。从图2（a）可以看出，各单元修正系数的均值与假定的工况一致。同时，在图2（b）中可以看出，除了3，4，5单元的标准差接近0.02之外，1，2，6，7单元的修正系数标准差均接近0.01。这些结果表明，由于测量误差的存在，实际上没有发生变化的单元弹性模量修正值也出现了标准差。这种现象主要是由模拟测量的误差引起的，并且在随机模型修正中通常不可避免。利用所提出的方法和MC方法，1，3，4，5单元的修正系数的概率密度函数如图3所示。从图3中可以看出，所提的方法得到的修正系数的概率密度函数曲线与MC方法的概率密度函数曲线非常吻合。

进一步验证模型修正结果的有效性。将本文提出的方法得到的统计修正参数代入式（20）并求解，可以得到修正后结构的随机响应。表1比较了修正前后结构频率均值的误差。结果表明结构的测量频率均值和修正频率均值误差几乎为零。但是对于模型修正，仅比较均值无法有效说明修正结果的可靠性，需要从全概率上进行充分的比较，比较结果如图4所示。图4显示前5阶修正后的计算频率与仿真的测量结果非常吻合。另外，前5阶修正后的计算振型的均值和标准差分别绘制在图5和6中。从图5中可以看出，本文方法修正的振型均值与模拟的测量振型均值结果几乎一致。从图6中还发现，对于前5阶振型，修正的振型标准差非常接近于模拟测量振型的标准差。这些结果都验证了所提出的随机模型修正方法的有效性。

3 结论

本文提出了一种基于随机有限元方法的随机模型修正方法。该方法建立了随机模型修正的新框架，包括随机模型修正方程的建立，随机修正方程的求解，以及修正结果的验证。它可以看作是确定性有限元模型修正方法在概率领域中的自然扩展。

从建立的随机模型修正方程，可以看出修正系数的不确定性来自随机测量误差。混合摄动-伽辽金法和正则化技术保证了随机修正方程解的精确性和唯一性。仿真算例说明，用该方法修正后的有限元模型能很好地重现随机测量结果。在获得修正系数的过程中，本文提出的方法仅需要不高于十次的有限元计算，就可以达到和十万次确定性的蒙特卡洛模拟相同的结果，显示出所提出方法的高效性。

参考文献：

[1] Friswell M I， Mottershead J E. Finite Element Model Updating in Structural Dynamics[M]. Dordrecht：Kluwer Academic Press， 1995.

[2] Mares C，Mottershead J E. Friswell M I. Stochastic model updating：Part 1-theory and simulected example[J].Mechanical System & Signal Processing，2006，20（7）：1074-1095.

[3] Beck J L， Katafygiotis L S. Updating models and their uncertainties-I： Bayesian statistical framework[J]. Journal of Engineering Mechanics，1998，124（4）：455-461.

[4] Katafygiotis L S，Beck J L. Updating models and their uncertainties—II： Model identifiability[J]. Journal of Engineering Mechanics，1998，124（4）： 463-467.

[5] Wan H P， Ren W X. Stochastic model updating utilizing Bayesian approach and Gaussian process model[J]. Mechanical System & Signal Processing，2016，70：245-268.

[6] Hua X G， Ni Y Q， Chen Z Q， et al. An improved perturbation method for stochastic finite element model updating[J]. International Journal for Numerical Methods in Engineering， 2008，73：1845-1864.

[7] 陳喆，何欢，陈国平，等. 考虑不确定性因素的有限元模型修正方法研究[J]. 振动工程学报， 2017，30（6）：921-928.

Chen Z， He H， Chen G P， et al. The research of finite element model updating method considering the uncertainty[J]. Journal of Vibration Engineering， 2017， 30（6）：921-928.

[8] Wu Z， Huang B， Li Y， et al. A statistical model updating method of beam structures with random parameters under static load [J]. Applied Sciences， 2017， 7（6）：601.

[9] Li Y J， Huang B， Li C Q.， Hybrid perturbation-Galerkin methods for structural reliability analysis[J]. Probabilistic Engineering Mechanics，2017，48：59-67.

[10] 张纯，宋固全. 去噪正则化模型修正方法在桥梁损伤识别中的应用[J]. 振动工程学报， 2012， 25（1）：97-102.

Zhang Chun， Song Gu-Quan. Bridge damage identification by finite element model updating with Tikhonov regularization and wavelet denoising[J]. Journal of Vibration Engineering， 2012， 25（1）：97-102.

[11] Ahmadian H， Mottershead J E， Friswell M I. Regularization methods for finite element model updating[J]. Mechanical Systems & Signal Processing，1998，12（1）： 47-64.

[12] Ren W X. A singular value decomposition based truncation algorithm in solving the structural damage equations[J]. Acta Mechanica Solida Sinica，2005，18（2）：181-188.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。