《经验快速谱峭度及其在滚动轴承故障诊断中的应用》-工学论文，振动工程论文-论文范文参考-科学狗论文网

标题

经验快速谱峭度及其在滚动轴承故障诊断中的应用

范文

张坤胥永刚马朝永张浩盛志鹏

摘要：快速谱峭度（Fast Kurtogram，FK）通过构造有限冲击响应滤波器从频谱上将信号二分或三分为几个不同频带的分量后，判断每个分量的谱峭度大小以提取调制信息。该方法运算速度很快，但有时包含故障信息的频段无法被均分的谱峭度图容纳，甚至可能导致提取出的分量中无法检测到明显的故障信息。提出一种新的频谱边界划分方法用以优化快速谱峭度，并称之为经验快速谱峭度（Empirical Fast Kurtogram，EFK）。首先，将信号频谱的傅里叶变换函数中代表频谱趋势的成分提取出来，并搜索其极小值点序列;然后，以极小值点在频谱中的位置作为频谱划分的边界，采用Meyer小波构造滤波器并重构信号分量以求取峭度;最终，构造出一种新的快速谱峭度图，选择谱峭度最大的频段提取故障信息。该方法依据信号频谱的趋势划分边界可以有效地避免由于均分频谱导致的不合理现象，模拟信号及滚动轴承内圈、外圈故障信号证明了该方法的有效性。

关键词：故障诊断;滚动轴承;快速谱峭度;经验快速谱峭度;频谱趋势

中图分类号：TH165+。3;TH133.33文献标志码：A 文章编号：1004-4523（2020）03-0636-07

DOI：10.16385/j.cnki.issn.1004-4523.2020.03.024

引言

机械自动化在现代工业体系中占据主体地位，机械零部件运行状态的实时监控越来越重要。作为旋转机械中必不可少且易损的零件之一的滚动轴承得到了深入的研究和广泛的应用。一个健康的轴承是设备正常运转的基础，而容易损坏并出现故障的轴承也是导致设备运行失效最大的隐患之一。因此，实现简单、高效、实时地监测轴承状态并诊断故障非常必要。旋转机械出现故障时由于故障位置变形会导致重复碰撞而产生周期性冲击，提取信号中包含的冲击分量，可以提高故障诊断的速度和准确率。

Antoni正式给出了谱峭度的数学定义，将SK定义为能量归一化的四阶谱累积量，详细阐述了谱峭度的相关理论，并证明了这种定义对加噪声中非平稳信号的特征检测有很好的效果，提出了基于傅里叶变换的快速谱峭度（Fast Kurtogram，FK）概念并得到广泛应用。蒋超等对总体平均经验模式分解获取的每一个IMF分量求取快速谱峭度图，筛选最大峭度所在频带以抑制干扰并提取故障信息。类似地，彭畅等在求取IMF的快速谱峭度图之前，采用度量因子将最能表征故障的IMF分量筛选出来，可以省去大量无效耗时。

经过学者研究，快速谱峭度方法也有它的弊端：均分频谱的方法造成所求的中心频率和带宽从理论上难以被合理地解释;在一定条件下该方法的计算结果不能真实地反映信号的实际情况。针对这个问题，部分学者进行了专门的研究，并提出自适应频带划分方法及最优边界选择方法。Wang等通过将右扩展窗口合并并自适应地确定滤波器的带宽和中心频率来最大化滤波后的信号峭度。在另一种自适应谱峭度方法中，选择Morlet小波来构造滤波器组，其中心频率由小波相关滤波来定义。通过筛选滤波器组中不同的带宽滤波器可得到能够提取信号瞬变信息的最优滤波器。Protugram方法在计算最优带宽后，通过扫频求出中心频率。上述方法虽然一定程度地实现了自适应并优化了边界，但都有一定的局限性，如：计算方法复杂导致耗时增加;在合并窗口之前构造滤波器的方法与Antoni的平均分割窗体的方法在原理上相同，遗传了原始方法的缺陷;计算最优带宽的浮动比较大，而且扫频的过程成几何倍增加了运算量及运算时间，使得该方法难以满足在线故障检测的需求。因此，在快速谱峭度领域探索一种更加合理的自适应方法非常必要。

本文提出的经验快速谱峭度（Empirical FastKurtogram，EFK）采用两次快速傅里叶变换提取不同的趋势成分求取趋势极小值代替FK中均分频谱的方法;采用Meyer小波构造滤波器代替FIR滤波器重构信号分量;优化了频谱划分边界的方式，简化了参数设置步骤，使得中心频率及带宽更加合理。研究结果表明，该算法运行效率高，有效避免了FK的传统缺陷，可以应用于轴承故障诊断中。

1 快速谱峭度及其不足

1.1 快速谱峭度

周期性冲击信号有确定的中心频率及边频带宽，这两个指标同时也是计算谱峭度的关键，因此选取合适的共振频带成为了精准诊断的前提条件之一。

Antoni提出的快速谱峭度算法将信号的谱峭度表征在（f，△f）平面上，其中心频率f和带宽△f的最佳组合可以使峭度最大。该方法采用频带交替二分法或三分法对信号进行分解，以构建的树状带通滤波器组为核心从频谱上划分边界;对信号的分解及滤波主要采用短时傅里叶变换（STFT）与有限冲击响应（FIR）滤波器;滤波后可获得一组高频、低频信号;求取滤波后各分量的峭度并用不同颜色表示峭度大小即快速谱峭度图。

1.2 快速谱峭度的不足

2 经验快速谱峭度算法

本文针对FK的不足，在频带划分部分进行了讨论和优化，提出一种新的方法以改进快速谱峭度：

（a）初始化重构点数ResCot1=5，累加点数AddCot=5，截止点数EndCot=60，j=1;

（b）设含噪声的周期性冲击信号为y（t），计算频谱Y（f）及关键函数K（f）：

y（f）=FFT（y（z））（1）

K（f）=FFT（Y（f））（2）

其中，FFT为快速傅里叶变换。

（c）根据重构点数ResCotj计算频谱的趋势成分Tcj（f）（2.1节阐述了这种方法的详细步骤）

其中，iFFT为逆快速傅里叶变换。

（e）選择Meyer小波作为基函数并将二维边界数组归一化至[0，π]，建自适应滤波器分解信号（2.2介绍了基于Meyer小波的分量重构方法）;

（f）求信号分量的峭度值，绘制经验快速谱峭度图;取出峭度最大的分量求包络谱，提取故障信息。

由于上述初始化重构点数、累加点数、截止点数均为多次实验后的经验指定，需要后续研究从理论上证明其合理性。因此本文将这种方法命名为经验快速谱峭度。流程如图2所示。

2.1 基于关键函数的趋势估计法

基于关键函数的趋势估计法源于傅里叶变换及逆变换，理论基础扎实且耗时较少，可用于提取频谱的趋势。频谱趋势可以较合理地拟合每一簇可能包含冲击信息的类调制信息，因此该方法可一定程度地将调制信息保留并剔除无用成分。

如何选择最佳点数进行傅里叶逆变换是能否得到理想结果的关键。图3为信号频谱与关键函数。取4（A），10（B），30（C），100（D），300（E）共5组重构点数进行傅里叶逆变换，重构点数的位置如图3所示。

不同的趋势成分会出现不同的划分结果。图4为傅里叶逆变换后的5组趋势成分及其最小值点对应的边界。当ResCot;较小时趋势成分简单，频谱被划分为较少区域，如A，B。当ResCot;较大时趋势成分复杂，包含的极值点也很多，并且频谱将被划分为较多区域，如D，E。因此，当所取重构点数小于5时，频域无法被划分为更少频段，无意义;当所取重构点数太大时，频域被划分过于详细，也无意义。本文以5为初始重构点数，并且以5个点数累加重构;当重构点数大于60时终止。

2.2 基于Meyer小波的分量重构方法

根据Meyer小波的构造方法为每一个频段构造一个合适的带通滤波器以提取对应频段中的信号以备信号重构。在频段两条边界处设计一组相互正交的三角函数，在频段内设计一个不变的常量。定义经验尺度函数和经验小波函数：

2.3 谱峭度简介

谱峭度对信号中的冲击信息非常敏感，常应用于轴承和齿轮的故障诊断。谱峭度定义为四阶谱归一化累积量，表示概率密度函数的峰值

3 仿真信号分析

采用FK方法处理该信号，如图6所示。信号从频域被划分为10个等级。峭度值最大的频段位于Level 4.6，中心频率为4791.67Hz，与实际中心频率相差近200Hz。提取此分量，波形如图6所示，可看到模糊的周期性冲击现象。包络谱中可找到特征频率及2倍频。该方法求取中心频率有一定的误差，同时诊断效果一般。

采用本文提出的EFK方法处理该信号，如图7所示。重构点数在从5增加到50的过程中，频谱被划分为数量不同的11个区域。当ResCot=25时峭度值最大，提取此分量的波形如图7所示，有一定的周期性且噪声比FK结果小很多。包络谱中包含特征频率，且可找到2倍、3倍、4倍等高倍频。故障信息明显，且中心频率f=5092.8Hz与实际中心频率非常接近。考虑噪声影响，该误差可以接受。因此，该方法适用于含噪声及周期性冲击信号。

4 工程应用

采用图8所示的故障试验台采集型号为6307的滚动轴承外圈故障振动信号。电机转速为1496r/min，采样频率15360Hz。计算求得故障特征频率为76.88Hz。

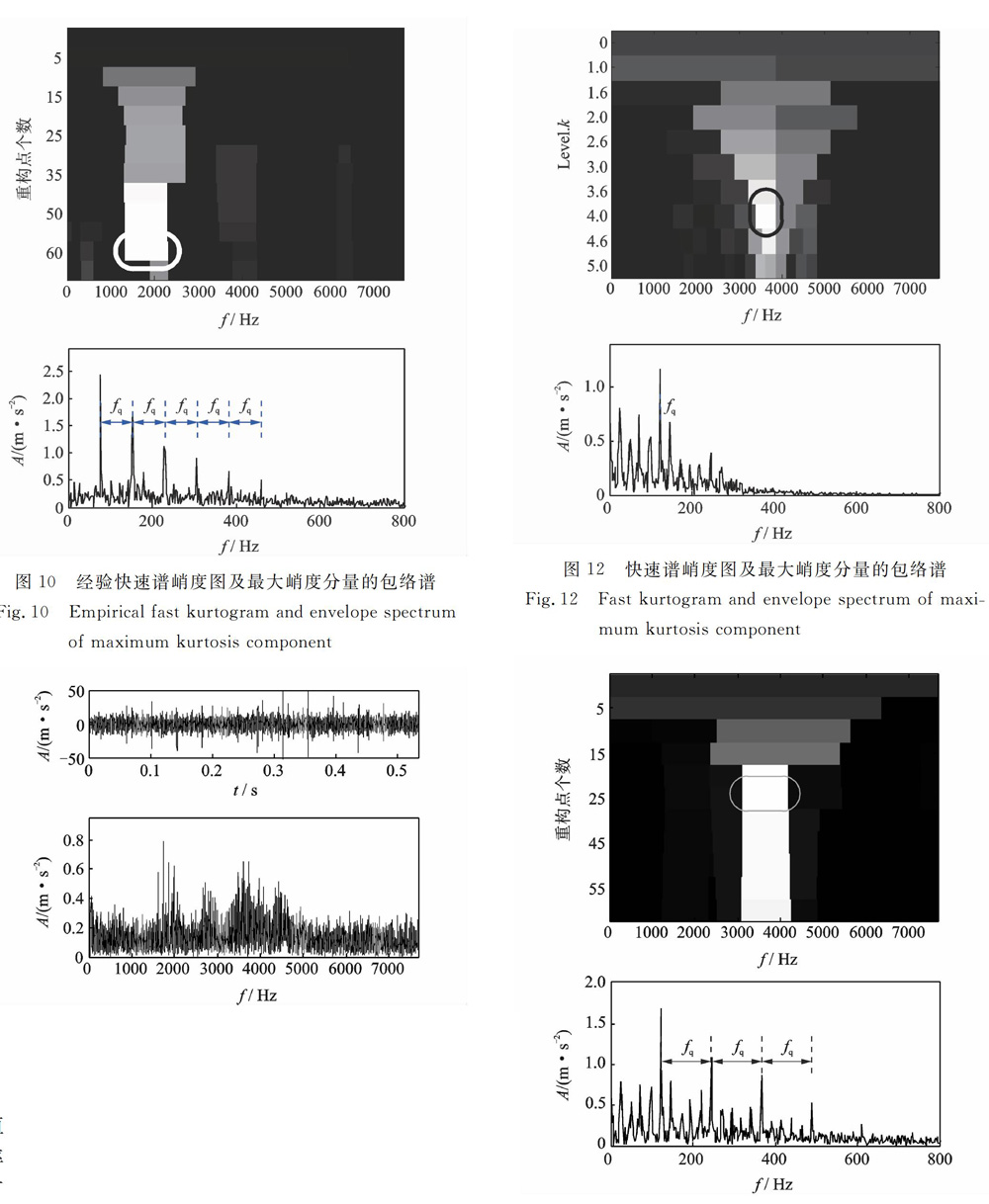
FK处理后，在Level 4.6可找到峭度最大的频段。提取此分量并求包络谱，结果如图9所示，可找到特征频率及其2倍频，但无法找到高倍频成分。利用本文所提EFK方法处理该信号时，当重构点数为60时获得最大峭度，此时中心频率与FK方法接近。提取此分量并求包络谱可找到特征频率及2，3，4等高倍频，故障特征信息较FK方法更为明显（如图10所示）。

采用图8试验台，另取相同型号滚动轴承并预置内圈故障，采集振动信号。电机转速为1496r/min，采样频率15360Hz。该轴承内圈转频为24.9Hz，故障特征频率为122.5Hz，信号的波形图及频谱如图11所示。采用快速谱峭度处理该信号，并且提取位于Level 4的峭度最大的分量，计算包络谱如图12所示。可找到内圈故障特征频率，但无法找到其倍频成分，故障特征不明显。

采用EFK方法处理该信号，当重构点数ResCot ∈[20，60]时，虽然重构分量的个数不同但峭度值最大的分量所在的频段基本固定。提取峭度值最大的分量可发现包络谱中有比较明显的特征频率及多倍频。将EFK与FK的分析结果进行对比，可以发现EFK求取的结果更合理，提取的分量中噪音更少且冲击更明显，求取包络后可以得到更多倍频信息，展现的故障信息比较直观。由此可见，经验快速谱峭度方法适用于周期性冲击信号的特征提取。

5 结论

（1）提出了一种经验快速谱峭度方法，用于提取轴承或齿轮振动信号中的周期性冲击成分。

（2）通过一个仿真信号和两个实验信号验证了经验快速谱峭度方法可依據信号特征筛选最佳中心频率及带宽。

（3）将经验快速谱峭度应用于滚动轴承故障诊断，可以有效提取故障信息。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。