纵观新课程改革下的计算教学,笔者以为计算教学更应关注学生的兴趣和经验、需求和情感,要从学生的视角出发,从教学的需要出发,适时适宜地变换教师角色。
一、从学生的兴趣出发,扮演计算情境的创设者
以往的计算教学,不仅机械枯燥,而且教学模式更是一成不变,千篇一律。学生充当“计算器”,教师充当计算器的“指令者”。学生不能顾及计算方法的理解,更谈不上计算方法的探索与形成过程。新课程改革以来,提出了“生活中的计算”和“运用计算解决生活问题”等新的理念与举措,计算课堂出现了欣欣向荣、生动有趣的景象,收到了较好的教学效果。这就需要教师在计算课堂上有必要扮演计算情境的创设者的角色。
例如,教学“两位数乘两位数”时,出示情境:
引导学生观察并思考:从这家牛奶厂的信息中你知道订一份牛奶一个月需要多少钱?订两个月呢?订一个季度呢?在学生兴趣高昂时,教师追问:“你还会算订多长时间牛奶的价钱?”以便从学生口中生成到“求订一份牛奶半年以及一年要花多少钱”的问题情境。这样,不仅调动了学生学习的兴趣,也帮助学生巩固了两位数乘一位数的口算方法,为两位数乘两位数笔算打下基础。同时,也帮助学生回忆了年月日的相关知识,使数学各个领域的知识有机地融合在一起。既提高了学生解决生活问题的能力,也为学生理解计算算理提供了现实依据和思维支撑,发挥了情境在数学教学中应有的作用。
二、从学生的经验出发,扮演计算策略的引路者
“计算”实际上是伴随着学生的成长而共同发展的。只是由于人的差异性,才导致学生计算能力的差异性。但对于每一位学生的成长经历或多或少都积累了一定的计算经验。回归到刚才的计算情境,当学生建构出“订一份牛奶一年要花多少钱”的问题情境时,教师引导学生列出28×12的算式。面对这样新的计算内容,在上面问题情境的启发之下,学生想出以下几种方法:
生:把每个月订牛奶的28元依次加起来。当学生说完,教师相机在黑板上板书:28+28+28+28+28+28+28+28+28+28+28+28。(学生还没说完,下面学生群体中已发出不耐烦的声音“太麻烦”。)
但正是由于受到这名学生的启发,生说出自己的想法:先算订一个季度牛奶的价钱再求订一年牛奶的价钱。教师引导学生列出算式:28×3=84,84×4=336。(此时教师故意带领学生口算得数时表现出很难算的表情。)
继而,学生又说出先算出订半年牛奶的价钱再算出订一年牛奶的价钱,教师同样要求学生给出算式:28×6=168,168×2=336。(在口算每一步得数时,教师依然流露出很难算的神态。)
细心聪明的学生已经注意观察到教师的神态。于是学生又说出先算出订10个月和订2个月牛奶各需要多少钱,再合起来。教师同样要求给出算式:28×10=280,28×2=56,280+56=336。(在口算每一步得数时,教师脸上绽放出轻松快慰的神情。)
这一体验过程结束时,教师追问:“这几种方法都能算出一年订牛奶的价钱,你们喜欢哪种方法?你认为一般情况下28×12应该用怎样的方法进行计算呢?”从刚才的活动中我们发现,学生的算法随着思维的展开也正进行着由直观到抽象、由视算到心算的转变,为笔算的引入作了充分的预设与铺垫。并带领学生进行几种计算策略的理解与优化及计算策略价值的体验。从而使学生亲身感受计算方法的多样与优劣,把学生的思路由“根据情境口算”逐步引向“抽象笔算”,进一步激发了学生探索更好更优的计算方法的欲望。
三、从学生的需求出发,扮演计算思路的点拨者
一旦学生的学习欲望被激发,思维就被激活,自然就会产生探索新知的需求。此时是知识建构的“最佳时机”。所以教师既要善于捕捉这一“最佳时机”,同时更要做好“最佳时机”的学习点拨者。笔者在教学“两位数乘两位数”时,设计了以下问题,从而引导学生的思维逐步走向深入:(1)如果用竖式计算你会有哪些疑问?(2)在乘法竖式计算过程中,是不是只有乘法运算,有没有其他运算?(3)在竖式书写时你想象中的乘法竖式应该是怎样的?(由于有了两位数乘一位数的经验,学生可能模仿与迁移)要求学生带着这样的问题尝试练习。学生练习完毕,教师搜集了三种竖式书写方法(还有相当一部分学生不会写):
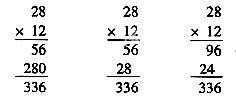
当方法揭示时,教师引导学生自己说出每一步求的是什么?并相机提出质疑:(1)在计算过程中你算出了几次积?(2)为什么要把两次积竖下来写?(3)把两次乘积相加时,前面要不要写加号,数位怎样对齐?
在教师的一步一步点拨之下,全体学生终于明白这几种算法的算理。虽然如此,在学生的心中又开始产生新的疑问:这三种方法都能算出正确结果,究竟如何书写才规范方便呢?学生探求新知的欲望再次被激起。此时学生的目光聚焦在教师身上。
四、从学生的情感出发,扮演计算方法的甄别者
如上所述28×12的结果出来之后,此时在学生的情感世界是多么希望教师能给出一种明确的竖式计算的方法,既方便书写,又方便计算的“计算法则”。当然此时“法则”的小结既不是教师的“指令”,也不是教师的强加,而是在学生已经充分理解算理的基础上自然形成的。因此,教师有必要带领学生作适当的引导与甄别。笔者是这样引导的:(1)第一步先算多少乘几?你是愿意用“2×28”还是愿意用“12×8”?(学生都说用“2×28”。一方面学生已有了两位数乘一位数的竖式计算的习惯和经验;另一方面,这样计算也符合人的观察习惯和思维习惯。)(2)用十位上“1×28”时,你们是愿意用十位上数字“1”直接乘“28”,还是先想十位上“1”表示1个十,用1个十去乘“28”?(学生齐答:“直接用1乘28。”)(3)如果直接用“1”乘“28”,数位怎样对齐,为什么?
由于学生在前面的学习活动中,已经历了两位数乘两位数的计算方法的形成过程并结合情境理解了现实意义。因而,通过这样引导与甄别,就能够有效地帮助学生实现从“现实情境里的算法具体含义”向“抽象的数学本质内容里的算法含义”的迁移。
综上所述,在计算教学中,教师只有从学生的视角出发,不断变换自身的角色,才能带领学生主动探索方法和经历知识的形成过程,促进学生的数学思维逐步走向深入。相信,只有用儿童的眼光看世界,用学生的眼光审视数学课堂,才能不断提高课堂教学的有效性,不断扩大学生的数学视野,不断满足学生的学习需求,不断培养学生的学习技能,也不断丰富学生的学习情感。
- 浅析里斯和特劳特的定位理论
- 基于大数据的企业价值创造路径分析
- 佩西的新人道主义理论对我国生态文明建设的启示
- 中国地区农业技术进步及其影响因素的空间计量分析
- 土地拍卖成交价格影响因素实证分析
- 快速城镇化对我国基础教育管理体制改革的新思考
- 贵州省旅游产业现状分析
- 基于EVA餐饮业上市公司的绩效评价
- 京津冀城市群产业结构演变特征
- “一带一路”战略下我国与中亚地区贸易合作的策略研究
- 以“一带一路”沿线区域文化一体化战略促进经济发展研究
- 浅析南通公路现代化及对经济发展的影响
- 统筹城乡基本医疗保险建设的策略研究
- 农村集体资产清产核资工作存在的问题及建议
- 浅析土地流转过程中的问题及相关对策
- “互联网+”背景下我国现代农业产业链及商业模式探析
- 河北省农村宅基地退出中农民权益保护问题研究
- 我国农村土地承包经营权确权问题及原因探究
- 城市汽车应急充电站物流规划成本影响研究
- 农村物流“最后一公里”浅析
- 刍议骨干员工激励机制的构建
- 高级会计师素质要求和能力培养相关问题研究
- 管理层股票期权激励的实施动因研究
- 兰州市科技型中小企业融资现状研究
- 论通货膨胀的形成原因及通货膨胀的成本
- get up to sth
- get used to
- get well
- get what you deserve
- get wind of
- get-wise
- get-wise-to
- get wise to
- get-with-it
- get worked up
- get worse
- get your act together
- get your breath back/catch your breath
- get your comeuppance
- get your feet wet
- get your fingers burnt
- get your hands on sth/sb
- get your head around/round sth
- get your head round
- get your hopes up
- get-your-irish-up
- get your just deserts
- geyser
- geyseral
- geysered
- 上古喻四为[l]、来母为[y]说
- 上古声母
- 上古声母系统
- 上古声调
- 上古声调系统
- 上古复辅音声母的讨论
- 上古时代
- 上古有清化鼻流音声母说
- 上古朝聘之礼
- 上古汉语
- 上古淳朴的社会
- 上古的帝王
- 上古贤明的君王
- 上古阴声韵无辅音尾说
- 上古阴声韵有辅音尾说
- 上古音
- 上古音系
- 上古音节结构
- 上古韵尾
- 上古韵母
- 上古韵部
- 上古韵部系统
- 上句不接下句
- 上可与玉皇同居，下可与乞儿共饭
- 上台