网站首页  词典首页

请输入您要查询的论文：

　

标题 让思维可见 让学习发生
范文 张玉平


[摘 要]为了让数学课堂体现数学的思维价值，为了让学生的学习真正发生，教师要借助观察、猜想以及操作等活动，帮助学生将机械的模仿记忆转变为自我的实践探索。以“圆的面积”的教学为例，通过比较、分析、概括等方式，使得学生经历新知的推导过程，做到真学习。
[关键词]圆的面积;数学思维;小学数学
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2017）26-0016-02
特级教师窦桂梅说过“教人语文，莫如以语文教人”，同样的，我们也可以说：“教人数学，莫如以数学（思维）教人。”下面将以“圆的面积”这一课为例，谈谈什么样的教学才是“数学（思维）教人”。
【片段一】
师（出示两个图形：一个是半径为15cm的圆，另一个是边长为30cm的正方形（正方形被报纸遮住了）谁来介绍一下这个圆？
生1：这是一个圆心为O，半径为15cm的圆。
师：圆的直径和周长各是多少？
生2：直径为30cm，周长为94.2cm。
师：今天我们将要学习的是圆的面积。老师用报纸遮住了一个平面图形，它与今天的学习内容有很大的关联，你能猜出是什么图形吗？
生3：正方形。因为正方形里正好可以画一个很大的圆。
师（揭开报纸，出示正方形）：看来正方形和圆果然存在一定的关系。这个正方形和圆的面积哪个更大？
生4：正方形，因为正方形里面正好可以画一个圆。
师：显然，正方形的面积大。能确定这个圆就是正方形里最大的圆吗？为什么？
生5：不能，因为没有写出正方形的边长是多少，所以不能比较它们的大小是否相等。
师：现在老师给出相应的数据，你能确定这个圆就是正方形里最大的圆吗？
生6：圆的直径是30厘米，正方形的边长是30厘米，所以这个圆是正方形里最大的圆。
师（补充）：显然，这个圆的面积比这个正方形的面积小。
【自悟：在“圆”这一章节的三节课里，“圆的面积”这节课我是最没有把握的。因为我不知道学生该如何去认识圆的面积，又该如何推导圆的面积，他们是否能理解教材上给出的方法，等等，这一系列的问题一直困扰着我。因此，对于这节课的教学，我做的都是“软设计”，就是跟着学生的思维走，随时调整课堂教学的走向。于是，课始我用一个猜图形的游戏，引导学生关注正方形与正方形内最大的圆的面积大小，为进一步推导圆的面积指明方向。】
【片段二】
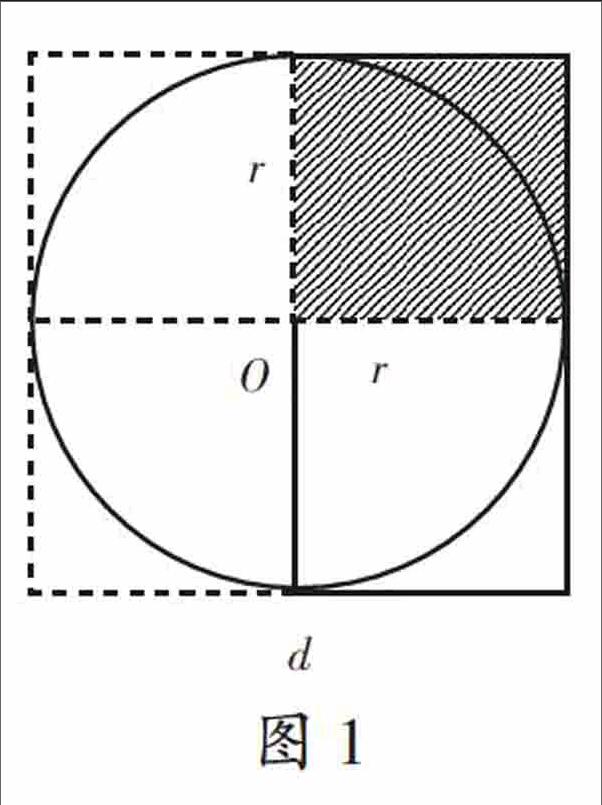
师：我们已经知道这个圆是正方形里最大的圆，它的直径是30厘米。假如没有给出这个正方形边长的具体数值，只知道正方形的边长是d，那么正方形的面积是——


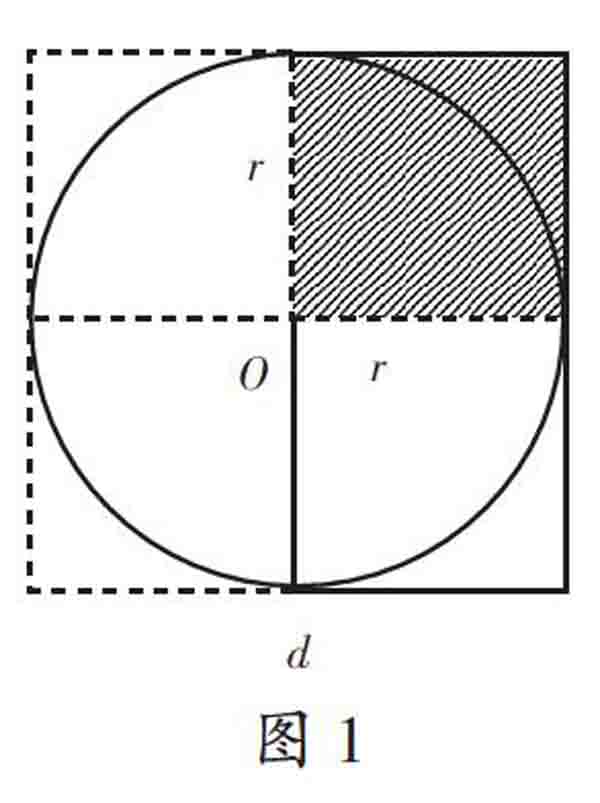
生1：d2。
师：还可以怎么说？
生2：4个r2。
师：我用虚线把r2标出来。
师：你觉得图1中的圆的面积是多少？
生3：圆的面积比r2的3倍多一些。
生4：圆的面积比r2的4倍少一些。
师：我们知道C除以d就等于圆周率π，那么■=π吗？
师：这个问号会是r2吗？
【自悟：在圆内，r2是一个看不见也摸不着的东西，这给学生的理解造成很大的障碍。将正方形内最大的圆与该正方形的面积进行大小比较，就可以通过它们之间的关系把正方形的面积分为四块r2，这为学生进一步理解r2打下了坚实的基础，学生能从观察与思考中猜想圆的面积是r2的三倍左右。同时，让学生结合圆的周长公式猜想面积公式“C/d=π→S/r2=π”，能够提升学生对圆周率的理性认识。】
【片段三】
师：想一想，平行四边形面积公式是怎么推导出来的？
生1：先把平行四边形拼成一个长方形。
师：三角形的面积公式是怎么推导出来的？
生2：也是通过拼的方法。
师：平行四边形和三角形的面积公式都是利用已知图形拼一拼、剪一剪后得到的，那梯形的面积公式是怎么推导出来的？
生3：也是通过拼的方法。
师：也就是说，我们总是把未知图形转化成已经学过的图形来推导，今天我们继续用这个方法来推导圆的面积公式。
师：前一节课我们知道把一个正方形对折，再对折，然后剪得的图形会越来越接近一个圆，那么，怎么把圆进行剪和拼才能够得到我们学习过的图形？
生4：对折两次后再剪。
生5：对折四次后再剪。
师：有剪刀的同学请试着操作，请先剪那个16等分的圆，不要剪32等分的圆。剪了以后想一想，我们怎么拼才能得到一个以前学过的图形？
（学生操作）
师：请拼出平行四边形的同学描述是怎么拼出来的。
生6：把圆平均分成16份，可以将16个扇形拼成一个平行四边形。
师：平均分成16份，剪出扇形，这两种颜色（黄色和粉色）的扇形應该怎么拼？
生7：黄色扇形的尖朝上，粉红色扇形的尖朝下。
师：将两种颜色间隔排列，的确可以拼成一个近似的平行四边形。
师：有同学拼成长方形，请说说是怎么拼出来的。
生8：用15个三角形先拼成一个近似的平行四边形，剩下的一个一分为二，拼在两边，就得到一个近似的长方形。
师：这个近似的长方形的长和宽与圆有什么关系？
生8：宽是圆的半径，长是半圆的周长。
生9：应该说长方形的长是圆周长的一半。
师：说得很准确，应该是圆周长的一半，不是半圆的周长。如果把圆平均分成32份、64份、128份……拼成的图形是不是越来越接近长方形？那么圆的面积公式能推导出来了吗？
生10：圆周长的一半是πr，再乘以r，就是πr2。（教师板书：S=πr2）
师：我们还可以把剪出来的扇形看成是一个三角形，三角形的面积是底乘高除以r2。沿着这个思路能不能推导出圆的面积公式？
生11：可以。一个小三角形的面积是16分之2πr，将其乘以r再除2，也就是πr2/16，再乘以16就是πr2。
师：现在请大家求出黑板上这个圆的面积。
生12：15×15×3.14=706.5（cm2）。
师：这是一个圆心为O，半径为15cm，直径为30cm，周长为94.2cm，面积为706.5cm2的圓。
【自悟：数学课程标准指出：“有效的数学学习活动不能单纯地依赖模仿与记忆，动手实践、自主探索与合作交流是学生学习数学的重要方式。”学生经历了剪拼的过程，想象就有了根基，就能在不同的认知中把圆转化为平行四边形、长方形和三角形，从而极大地丰富了圆的面积公式的推导方式。正是在这样多元的思考表达中，学生的思维进入了更深的层次，学习才真正发生。】
【片段四】
师：如果这个正方形的面积是100平方厘米，那么正方形里最大的圆的面积是多少？
生1：78.5平方厘米。
师：请说说你是怎么算的。
生1：正方形的面积是100平方厘米，正方形的边长就是10厘米，那么圆的直径也是10厘米，半径就是5厘米，圆的面积等于πr2 ，所以就得到π乘5的平方，就是78.5平方厘米。
师：如果这个正方形的面积是10平方厘米，那么正方形里最大的圆的面积是多少？
生2：正方形的面积是10平方厘米，那么边长是……（学生说不出来）
师：能用其他方法解决吗？
生3：圆的面积是7.85平方厘米。
师：请说说理由。
生4：除以10就可以了，原来的面积是现在的10倍。
师：按原来的方法进行计算有一定的难度，而把数据缩小10倍就能得到答案了。（教师板书：3.14×（10÷4）=7.85）
师：这里的“10÷4”是什么？与r2 有什么关系？
生5：正方形的面积是10，那么10÷4=2.5，2.5就是r2 。
师：也就是说，我们在计算圆的面积时，不是一定要知道圆的半径是多少，只要知道半径的平方是多少就可以了。这真是“思路一转天地宽”呀！
【自悟：对于学生来说，求圆的面积要按公式来套，也就是要先知道圆的半径或直径，这样的认知很容易造成学生思维的定式。通过两个不一样的题目，引发学生的认知冲突，让学生有了进一步学习的欲望，因为之前有了对r2的深入认识，学生能想到用整体思维去解决问题，这样的问题能引领学生对整个知识进行回顾，培养学生不断挑战和探索的科学精神。】
总之，教师在教学中要引导学生经历观察、猜想、操作、验证等过程，让学生通过知识迁移，主动将新知与旧知进行联系，通过比较、分析、概括等方式，自主经历新知的推导过程，这才是真正的让思维可见、让学习发生。
（责编 童 夏）
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2025/2/6 6:02:19