网站首页  词典首页

请输入您要查询的论文：

　

标题 求解多重二次背包问题的改进遗传算法
范文 刘梦佳+向凤红+毛剑琳+郭宁



摘要：
多重二次背包问题，旨在将具有单独价值与协作价值的对象分配到一组容量有限的背包中，使总利润最大化，是一种具有广泛应用的NP难组合优化问题。针对该问题提出一种引入自适应模式替换和贪心算法思想的改进遗传算法（IGA）。首先对初始种群进行自适应模式替换，使每代种群中的最好基因个体保存下来形成模式，替换原种群中质量较差的个体，通过设计贪婪算子改进贪心思想对问题进行排序，然后进行扰动交叉操作和双重选择变异操作，最后采用最大化修复策略以保证解的可行性。标准算例仿真结果表明，相比传统算法，IGA具有较强的寻优能力。
关键词：多重二次背包问题；自适应模式替换；贪心算法；遗传算法；最大化修复策略
DOIDOI：10.11907/rjdk.171999
中图分类号：TP312
文献标识码：A文章编号文章编号：16727800（2018）001004904
Abstract：The quadratic multiple knapsack problem （QMKP） consists in assigning objects with both individual and pairwise profits to a set of limited knapsacks in order to maximize the total profit. QMKP is a NPhard combinatorial optimization problem with a number of applications.To solve the problem，an improved genetic algorithm （IGA） introduced adaptive model of replacement and greedy algorithm is proposed.First， the algorithm used selfadaptive model of replacement to initial population so that made the best gene from each generation population individuals survived and formed model to replace the poor quality individuals of the original population.Then sorted the problem by changing the greedy thought through designing greedy operator. After that performed the disturbance cross operation and double selection mutation operation. Finally， to ensure the feasibility of the solution by using maximized repair strategy. In the numerical computation results on standard quadratic multiple knapsack problem instances，the IGA has stronger optimizing capacity than the traditional algorithms.
Key Words：quadratic multiple knapsack problem； selfadaptive replacement model； greedy algorithm； genetic algorithm； maximize repair strategies
0概述
多重二次背包問题（Quadratic Multiple Knapsack Problem，QMKP）是二次背包问题（Quadratic Knapsack Problem，QKP）与多重背包问题（Multiple Knapsack Problem， MKP）两个经典NP难题融合后的一个新问题，由Hiley和Julstrom[1]于2006年提出。目前，QMKP广泛应用于金融、库存管理、生产计划调度、机场车站布局、密码设计、通讯基站优化、集成电路设计等方面，在最近几年也得到了学者的广泛关注[2]。现有两种求解方法为精确方法和启发式方法。较具代表性的精确算法有2012年Quadri等[3]提出的分支定界精确算法及Wang等[4]提出的具有线性表示的分支定界法，精确算法都只能求解小规模QMKP，难以满足实际需求，所以启发式法通常用于在合理的计算时间内找到多重二次背包的近似解[5]。如Hiley和Julstrom[1]提出了3种用于解决多重二次背包的方法，即贪婪启发式算法、随机爬山算法和具有爬山算子的遗传算法（其中对所选父节点交叉算子通常保留对象到背包的分配）。Singh和Baghel[6]提出了一种稳态分组遗传算法解决QMKP。算法思想反复选择两个父代交叉产生子代去替代种群中较差个体，将具有最大利润值的背包从所选父代遗传到子代，种群每次迭代并不完全被替换，始终保持拥有较优个体。另外，Sarac和Sipahioglu[7]使用另一种遗传算法解决QMKP，此算法使用互相交换两个随机选择的父代对象分配特殊交叉方式。2010年Sipahioglu等[7]提出了一种基于可行解的次梯度遗传算法（MSGGA），次梯度方法在处理约束时不必考虑惩罚参数，处理相对简单。另外，2010年Sundar[8]针对QMKP引入了人工蜂群算法与局部搜索（SSABC）的组合。人工蜂群算法由于编码特点使其更适合处理连续优化问题，在处理组合优化问题上并不占优势。从上述文献看，出现的启发式算法多采用遗传算法，这些遗传算法中虽融入了不同算子用于改进性能，但随着迭代次数的增加，最优解变得越来越少，导致交叉和变异操作往往只能在最优解内部进行，遗传速度大大放缓，使其处理QMKP效果并不理想[9]。
本文算法首先重新设计传统的贪心算子，将问题用改进后的贪婪算法排序，为求解大规模QMKP奠定基础；然后引入自适应模式替换，使每代种群中的最好基因个体保存下来形成模式，引导种群的搜索方向，提高了搜索性能，避免了早熟现象的出现；接着进行选择、扰动交叉操作、双重选择变异操作；最后引入最大化修复策略，对不可行解进行修复，对可行解进行修正，最终更加有效地解决多重二次背包问题。
2.4自适应模式替代
为了提高遗传算法的搜索速度和寻找最优解的能力，本文在进行选择操作之前引入自适应模式替换操作。
模式是基于三值字符集{0，1，*}所产生的能描述某些结构相似的0、1字符串集的模板[10]。例如模式1**1（长度为4的串）描述了在位置1和位置4为“1”的字符串，即{1001，1011，1101，1111}。
模式替代就是通过记录每代种群中最好的几个个体生成模式采样空间，然后利用种群中的不确定字符“*”生成新个体，用生成的新个体替换原种群中质量较差的个体，使这些替换后的新个体经过交叉、变异之后仍能以较大的概率存活下来，从而保证优良基因的繁殖，引导种群的搜索方向[11]。传统模式替代的模式固定率是固定的，随着迭代次数的增加，较优个体越来越集中，模式中确定基因位越来越多，其结构也越来越相似，这就影响了迭代后期种群的多样性及新个体的生成[12]。鉴于此，为保证模式中确定位数和不确定位数在整个迭代过程中保持相对稳定，本文结合自适应思想，采用自适应模式替代，规定了确定基因位和不确定基因位的产生方式，即设置自适应模式比Ra，若模式中确定基因位太多，可以提高Ra，减少确定的位数；若模式中确定基因位太少，则降低比例数Ra，增加确定的位数，以此对模式进行评估和校正。具体操作如下：
（1）考虑到计算量，本文设置每隔20代进行一次模式生成。
（2）将种群适应值按降序排列的个体集中前ML个（模式采样空间的个体数，本文取50）个体记录下来进行统计，形成模式候选集。
（3）在模式采样空间里，计算种群中所有个体相同基因位上1和0所占比例之差的绝对值，记为基因差别比例Ca[12]。对各基因位的基因差别比例进行非升序排序。按照给定自适应模式比的初始值选出前r个基因位作为确定基因位，剩余基因位均为不确定基因位，将确定基因位与个体长度之比定义为自适应模式比Ra。
例如：模式空间的较优个体为：11 010，01 110，10 010，11 001， 10 110，那么各基因位上0和1所占比例分别为：0.2、0.8，0.4、0.6，0.6、0.4，0.2、0.8，0.8、0.2，0和1所占比例之差的绝对值分别为0.6，0.2，0.2，0.6，0.6，若给定的自适应模式比的初始值为Ra=0.5，则确定基因位是1、4、5，不确定基因位为2和3，更新后的Ra=0.6。
计算被记录个体每一基因位上0（或1）的个数占当前种群此基因位总字符数的比例，若超过Ra，则该基因位值为0（或1），否则为*，由此得到采样空间的模式，如上例中生成模式为1**10，其中被确定为0或1的基因位称为个体的优良基因。
（4）将具有优良基因的新个体加入到原种群中，计算所有个体的适应度，并按适应度进行降序排列。然后取前PopSize个个体作为当前种群，由此替代原种群中质量较差的个体。在保证提高寻优能力的同时防止早熟。
2.5扰动交叉与双重选择变异操作
在遗传算法中，交叉和变异操作主要是产生新的个体，维持种群多样性。为增强种群多樣性，提高算法的局部搜索能力，必须对交叉操作产生的新个体进行筛选，防止模式相差较小的个体过多地进入候选集。具体操作如下：
传统的变异操作根据变异概率Pm进行按位随机变异，当Pm决定了变异个体后，该个体所变异的基因位是随机的。对于二进制编码的个体来说，就是随机对某一基因位0变1或1变0，这对遗传算法的局部搜索性能并没有较好的提高。本文按照基因差别比例Ca进行变异。变异概率Pm决定变异个体后，由Ca决定进行变异的基因位，在此定义为双重选择的变异操作。首先，计算种群中各基因位上0和1所占比例之差的绝对值。例如：1 010，1 011，1 101，1 100，1 110，0 011，各基因位上的Ca分别为Ca1=2/3，Ca2=0，Ca3=1/3，Ca4=0。然后比较Ca值，Ca值越大的基因位进行变异的概率越大，这就在一定程度上决定了进行变异的基因位，避免早熟现象。
2.6最大化利用率修复策略
在遗传算法中，每一次的迭代都需要进行选择、交叉和变异操作，产生新个体，提高种群多样性，尽可能获得全局最优解。但是，经过这样一系列的操作后，生成的解可能超出约束条件，对此问题的处理方法通常有惩罚函数法和修复操作法。本文采用既考虑价值重量比又兼顾各背包容量利用率的最大化利用率修复策略，修复不可行解的同时修正可行解。首先对违反约束条件的解，按照价值密度递增的顺序依次减掉背包中的物品，直到满足约束条件为止。然后，对满足约束条件的解，按照价值密度递减的顺序将物品放入剩余容量最大的背包中，直到背包不能再装为止。这样既可以保证种群中每一个个体是正常编码的个体，又可以使其对应较优的可行解。
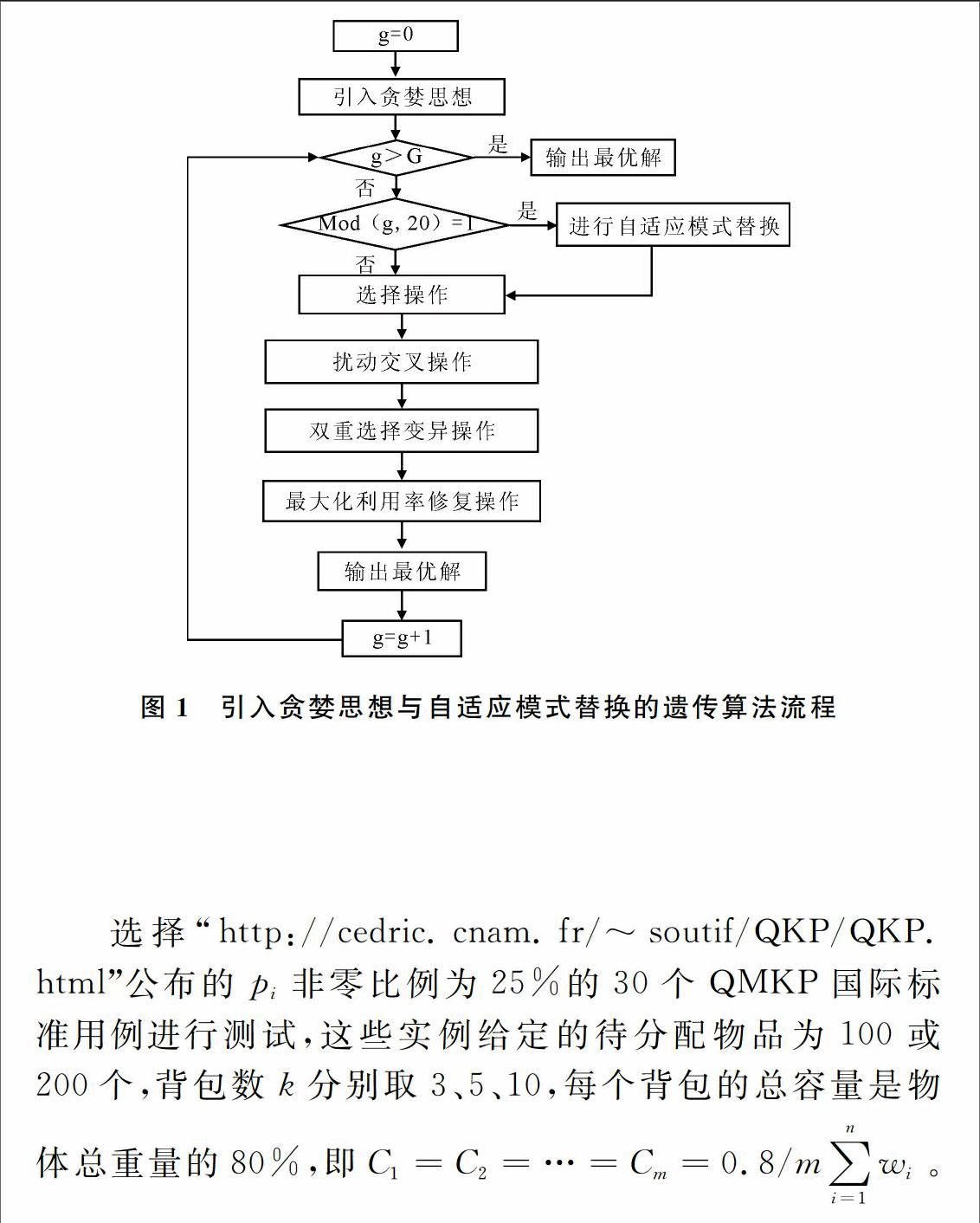
3改进的遗传算法具体流程
改进的遗传算法的具体流程如图1所示，其中g为迭代次数，G为最大迭代数。
4算例及结果分析
在本文使用的算例中，群体规模取PopSize=100，模式采样空间个体数取ML=50，自适应模式比的初始值取Ra=0.5，交叉概率取Pc=0.8，变异概率取Pm=0.2，最大迭代次数G=1 000，算法程序由MATLAB编码实现。
为验证本文算法的性能，将IGA与随机爬山算法（SHC）、具有爬山算子的遗传算法（HCGA）、人工蜂群算法（SSABC）进行比较，分别对30个测试用例独立运行40次，对比结果如表1及表2，其中Best表示40次求解所获最好的最优解在此称为最佳解，Avg表示40次最优解的平均值，SD为40次结果的标准偏差，4种算法中最好的平均值和最佳解用粗体突出显示。
由表1可以看出，4种算法对100维的15个标准实例求得的最佳解和平均值中，IGA求解的最佳解仅有2个不是最
优的，平均值仅有1个不是最好的，剩下的12个问题在最优值、平均值、标准偏差都优于其它算法。
由表2可以看出，200维测试中IGA求解的平均值和最优解各有4个比其它算法略低或相当，另9个测试问题的最优值、平均值、标准偏差都优于其它算法。
综合表1、表2，4种算法对30个标准实例求得的最佳解和平均值中，IGA求解的最佳解有24个是最优的，占所有最优解的80%，平均值有25个是最好的，占所有最好平均值的83.33%。且IGA算法的标准偏差更小一些，说明IGA算法在求解多重二次背包问题时具有一定的可行性和有效性。
5结语
本文提出了一种改进的遗传算法，首先设计了贪婪算子，引入价值密度，然后加入自适应模式替代操作，进行扰动交叉和双重选择变异，最后使用最大化利用率修复策略。提出的IGA算法局部搜索能力和全局搜索能力较强，能很好地保持种群多样性，避免了早熟现象的发生。通过实验仿真，验证了IGA算法具有较好的性能，说明了IGA的有效性和可行性。目前，本文只优化了协作价值非零比例为25%的情况，今后将对协作价值非零比例较大的多重二次背包问题继续研究。
参考文献：
[1]HILEY A， JULSTROM B A. The quadratic multiple knapsack problem and three heuristic approaches to it[C]. Proceedings of the 8th Annual Conference on Genetic and Evolutionary Computation.New York，2006.
[2]钱洁，王保华，郑建国，等.多重二次背包问题的量子进化求解算法[J].计算机学报， 2015（8）：15181529.
[3]DELLA CROCE F，QUADRI D.Improving an exact approach for solving separable integer quadratic knapsack problems[J].Journal of Combinatorial Optimization，2012，23（1）：2128.
[4]WANG H，KOCHENBERGER G，GLOVER F.A computational study on the quadratic knapsack problem with multiple constraints[J].Computers&Operations Research，2012，39（1）：311.
[5]J QIN， X XU， Q WU， TCE CHENG. Hybridization of tabu search with feasible and infeasible local searches for the quadratic multiple knapsack problem[J]. Computers & Operations Research，2016，66：199214.
[6]Y CHEN，JK HAO，F GLOVER. An evolutionary path relinking approach for the quadratic multiple knapsack problem[J].Elsevier Science Publishers B.V. 2016，92（C）：2334.
[7]SIPAHIOGLU A，SARAC T.Solving the generalizad quadratic multiple knapsack problem by using FMSG algorithm[C].Proceeding of the 24th Mini EURO Conference on Continuous Optimization and Informationbased Technologies in the Financial Sector，Izmir，Turkety，2010.
[8]SUNDAR S， SINGH A. A swarm intelligence approach to the quadratic multiple knapsack problem[J]. Lect Notes Comput Science，2010，6443：626633.
[9]X LIU，F XIANG，J MAO.An improved method for solving the largescale multidimensional 01 knapsack problem[C].International Conference on Electronics & Communication Systems. Coimbatore， INDIA，2014.
[10]于惠.遺传算法的改进研究及在背包问题中的应用[D].济南：山东师范大学，2009.
[11]李康顺，贾玉珍，张文生.一种基于模式替代的遗传算法解0/1背包问题[J].计算机应用研究，2009，26（2）：470471.
[12]王娜，向凤红，毛剑琳.改进的自适应遗传算法求解0/1背包问题[J].计算机应用，2012，32（6）：16821684.
（责任编辑：何丽）
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2024/12/23 1:34:45