网站首页  词典首页

请输入您要查询的论文：

　

标题 用“情境”激发学习兴趣，以 “问题”促进深度思考
范文 万兰平


[摘 要]学生是数学学习的主人，教师是数学学习的组织者、引导者与合作者。以“表面涂色的正方体”的教学为例，先通过在课堂中激发学生的学习兴趣，点燃学生学习的热情，从而促使学生主动学习，学会自主学习，再利用问题引发学生的思考，提高学生的数学思考力。
[关键词]情境；兴趣；问题；思考
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2018）02-0019-03
【背景】
“表面涂色的正方体”是苏教版教材六年级下册的内容，它是在学生已经学习了长方体和正方体的特征、体积计算公式等知识的基础上进行教学的。本节课的教学内容属于“综合与实践”领域。我在2015年第一次上这节内容时，学生缺乏兴致，思考流于表面，教学效果不佳。对此我进行了反思：课始就平铺直叙地出示教学内容，并不能激发学生的好奇心和学习兴趣，虽然后面给了学生充分的自主学习的时间和空间，但由于引导不力，导致学生的思维无法走向深入。于是，我与自己“同课异构”，再次执教这节课，采用“情境”激发学生的学习兴趣，以“问题”促进学生深度思考的方式进行教学，取得了良好的效果。
【教学实践】
我从学生喜爱和熟悉的正方体蛋糕入手，以蛋糕师傅切分蛋糕遇到的问题来促进学生思考，让学生在解决问题的过程中将思维不断引向深入。教学结果显示，在这样的教学情境下，学生敢于在课堂上大胆表达自己的想法，学习带来的自信洋溢在每一个学生的脸上！
一、创设情境，激发兴趣，引发思考
师：在这一单元中，我们学习了长方体和正方体的有关知识。如果留心观察，你就会发现长方体和正方体在生活中随处可见。
师：瞧，蛋糕师傅做的大蛋糕是什么形状？（ppt出示蛋糕图片）
生（齐）：蛋糕是正方体。
师：正方体的特征是什么？
生1：正方体有12条棱，6个面，8个顶点。
生2：正方体的12条棱是相等的，6个面都是一样的正方形。
师：很好！现在根据顾客的需要，蛋糕师傅要先把正方体蛋糕的6个面涂上巧克力，再把它切成小块的正方体形状来卖，将每条棱平均分成10份，切出的小正方体蛋糕6个面都有巧克力吗？
生3：小正方体蛋糕不可能6个面都有巧克力，因为只有大蛋糕外面有巧克力，刀切下去的那个面没有巧克力。
师：那小正方体蛋糕会有几个面涂有巧克力？
生4：有的是3个面涂有巧克力，有的是2个面涂有巧克力，有的是1个面涂有巧克力，还有的是6个面都没巧克力。
师：大家同意他的说法吗？同意的请举手。（学生都举手）
师：那3个面上涂有巧克力的小正方体蛋糕在哪？2面的又在哪？1个面的呢？谁能上来边说边指给大家看看。
生5：3个面涂有巧克力的小正方体蛋糕在角落上，2个面涂有巧克力的小正方体蛋糕在棱上，1个面涂有巧克力的小正方体蛋糕在每个面的中间。（学生一边说一边指着蛋糕）
师：他说的对吗？
（有的学生表示肯定，有的学生在犹豫）
师：他说的究竟正不正确呢？大家桌面都有蛋糕模具，拿起来看看，再仔细思考。
师：我们今天就来研究这个表面涂色的正方体中藏着的一些秘密。
（板书课题：表面涂色的正方体）
师：现在糕点师傅要把3面、2面、1面涂有巧克力的小正方体蛋糕分类装盒，每个盒子装一块蛋糕，每种盒子各要多少个呢？（ppt显示不同的蛋糕盒）谁能迅速把答案告诉糕点师傅？
【思考：此环节采用的生活情境是做蛋糕，这是学生熟悉的场景，因此能快速激活他们已有的生活经验，激发他们的学习兴趣。遇到小正方体蛋糕究竟有几个面涂有巧克力的问题时，学生能够迅速调出已有的相關经验，大多数学生能直接说出有3面涂色的、2面涂色的、1面涂色的和没有涂色的。在寻找3面涂色的、2面涂色的和1面涂色的小蛋糕在哪里时，为了让学生获得更多的体验，便可引导他们在模具上验证，有了这个模具，学生都积极主动地去观察、寻找、验证。最后，提出“要把蛋糕分盒装，每种盒子需要准备几个的问题”时，所有学生探究的兴致都被调动起来了。可见，数学是思维的体操，问题是思维的源头！】
二、有效问题，引导学生走向有序思考
师：先研究把正方体的棱长平均分成几份比较合适？为什么？
生1：我们先研究把正方体的棱长平均分成3份，因为平均分2份时不会出现2面涂色的小正方体。
……
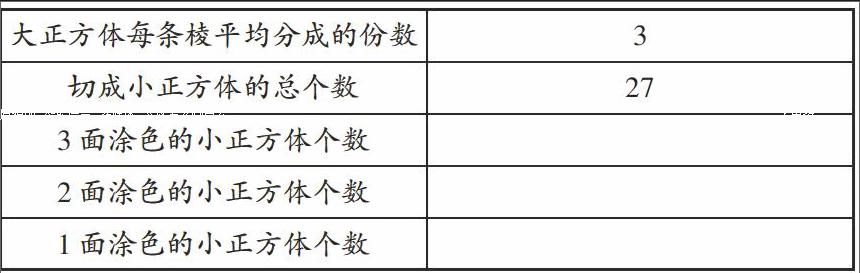
师：下面请结合手中的每条棱平均分成3份的学具，认真观察后独立思考下面2个问题：
（1）3面、2面、1面涂色的小正方体各在大正方体的什么位置？
（2）其中3面、2面、1面涂色的小正方体各有多少个？完成下表。
（要求学生独立完成后与同桌交流，最后全班交流）
【思考：根据学生的要求从把正方体每条棱平均分成3份开始研究。重点要研究的是3面、2面、1面涂色的小正方体各有多少个。对于这个环节的处理，我两次教学都是放手让学生自己去观察、思考、研究，所不同的是，第一次教学没有设置问题，只是让学生利用自己手中的学具直接找一找、数一数，结果大多数学生都在毫无目的地找和数，有不少学生漏数或重复数，全部对的学生寥寥无几，把正方体的每条棱平均分成n份后能得出答案的学生就更少了，最后的规律也只能是连蒙带猜了。究其原因，是此环节中缺少教师的引导，导致学生的思考浮于表面，无法深入。于是，我第二次教学时在此环节设置了2个问题，首先让学生再次确定3面、2面、1面涂色的小正方体各在大正方体的什么位置，旨在引导学生发现相同涂色正方体的所在位置的规律，在对应的位置寻找到相同的小正方体，从而进行有序地找和数。我在巡视时发现大多数学生都能够有序地进行找和数，经过同桌之间的交流，每一位学生都能够做到有序思考。显然，教师只有恰当地“引”，学生才能更好地“思”，学生的学习才能真实发生！】
三、深度追问，促进学生的思考走向深入
师：为什么把正方体的每条棱平均分成3份，而每条棱中间2面涂色的小正方体却只有1个呢？
生1：因为正方体的每条棱上两端的小正方体都是3面涂色的，所以3-2=1（个）。
师：是这样吗？请在学具上找到算式中的3、2、1。
师：研究了每条棱平均分成3份的小正方体，下面要研究把每条棱平均分成几份的小正方体？（4份）请各小组在组长的带领下利用学具进行研究，并完成表2（格式同表1，略）。
师：1面涂色的小正方体在大正方体的每个面的中间，每个面为什么会有4个？
生2：1面涂色的小正方体在正方体的每个面的中间有（4-2）×（4-2）=4（个）。
师：想一想，如果把正方体的棱平均分成5份，在正方体每个面中间的1面涂色的小正方体有多少个？
生3：如果把正方体的每条棱平均分成5份，大正方体每个面中间的1面涂色小正方体有（5-2）×（5-2）=9（个）。
【思考：经过上一个环节两个问题的引导，学生都能有序地找和数，但大多数还停留在数的层面，所以研究完每条棱平均分成3份的情况后，我提出问题：“为什么把正方体的每条棱平均份成3份，每条棱中间2面涂色的小正方体在却只有1个呢？”旨在引导学生进一步思考，从而发现每条棱平均分成的份数和2面涂色的个数之间的联系，推动学生的思考向更深的层次发展。同样研究完每条棱平均分成4份的情况后，我又问：“一面涂色的小正方体在大正方体的每个面的中间，每个面为什么会有4个？”引导学生发现每条棱平均分成的份数和每个面上1面涂色小正方体的个数之间的联系。到这里，教学目标似乎已经达成，但我并未收手，继续追问：“如果把正方体的棱平均分成5份，在大正方体每个面中间的1面涂色小正方体有多少个？”意在让学生在头脑中形成关于表面涂色的正方体的表象认知，促进学生抽象思维的发展。】
四、回歸生活问题，提升学生的数学思考力
师：糕点师傅切出的小蛋糕都包装了吗？没涂巧克力的小蛋糕的个数是否有什么规律？请课后继续研究。
【思考：在教学中，教师要以发展和提升学生的数学思考力为出发点。本节课上，经过自主学习、解决问题，学生能够发现蕴含在涂色正方体中的一些规律，为了进一步推动学生思考，最后又回到课始的糕点师傅包装小蛋糕的问题，让学生思考没涂巧克力的小蛋糕的个数有什么规律，旨在让学生运用课堂上获得的研究问题的方法，进一步研究和思考没涂巧克力的小蛋糕个数的规律，从而提升学生的数学思考力。】
【案例反思】
2016年我市教育专家提出了“让学引思”的教学理念，“让学引思”是基于德国哲学家海德格尔的“让学”理念提出的，其核心是为了改进学生的学习方式，它与数学课程标准的“学生是数学学习的主人，教师是数学学习的组织者、引导者与合作者”一脉相承。在教学过程中，我对此教育理念有了更深刻的理解和体会。
1.“让学”是指让学生成为学习的主人
“让学”并不仅仅是让给学生自主学习的时间和空间，更重要的激发学生学习的兴趣，点燃学生学习的热情，让学生从被动等待变成积极主动的学习，力求让学生的“学”真正发生。第二次教学时，我从学生熟悉的生活情境入手，随着情节的发展、问题的出现，学生探究的欲望被完全激发出来，学生情绪饱满地进入积极主动探索的状态，学生在观察、思考、讨论、操作等活动中的自主学习、协作学习和探究学习，呈现的是主人的姿态。
2.“问题”是“引思”的绳索
课堂上要想引发、引导、引领学生思考，保证他们大脑处于积极的思考状态，问题的设置就相当重要。本节课开始，蛋糕师傅的问题激发了学生主动探索的欲望，也引发了学生的思考，接下来的第一次研究活动中设计的问题“3面、2面、1面涂色的小正方体各在原正方体的什么位置？”就能引导学生有序思考从而发现规律，紧接着的两次追问也能引发学生深度思考 ，最后回归生活问题，更是引发了学生更深层次的思考，提升了学生的数学思考力。
（责编 金 铃）
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2024/12/23 4:12:12