网站首页  词典首页

请输入您要查询的论文：

　

标题 用于测试用例自动生成的遗传算法改进
范文 喻婧　易国洪



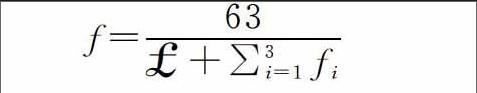
摘 要：探讨遗传算法的基本准则及其在软件测试中的应用，在此基础上对遗传算法进行改进。针对基本遗传算法中选择算子、交叉算子、突变算子的不确定性，以及容易陷入局部最优解和停滞的问题，提出SO、SACO、SCAMO算法。对改进的遗传算法和基础遗传算法进行比较。实验结果表明，改进的遗传算法比基础遗传算法自动生成测试用例的时间更短、效率更优。
关键词：软件测试；测试用例；遗传算法；选择算子；交叉算子；突变算子
中图分类号：TP311
文献标识码：A 文章编号：1672-7800（2015）005-0095-03
作者简介：喻婧（1991-），女，福建莆田人，武汉工程大学计算机科学与工程学院硕士研究生，研究方向为软件工程；易国洪（1970-），男，湖北武汉人，博士，武汉工程大学计算机科学与工程学院副教授、 硕士生导师，研究方向为软件工程、计算化学。
0 引言
据统计，软件测试的费用约占软件开发总成本的50%，实现软件测试过程的自动化成为必然趋势，而实现测试过程自动化的关键在于自动生成软件测试用例[1]。自动生成测试用例，将改变靠直觉、经验生成测试用例的传统做法，可显著提高软件测试效率，减轻编写大量测试用例的工作量。目前，软件测试自动化工具研究主要集中在测试用例执行和维护，以及测试覆盖度量等方面，测试用例自动生成。本文探讨基本遗传算法，针对其缺陷进行改进，并且通过实验验证改进算法的有效性和可行性。
1 基础遗传算法
遗传算法由美国John Holland教授提出，模拟了达尔文的生物进化过程中自然选择和计算模式。其主要特征为：能直接操作结构对象，不受导数和函数连续性的限制；有隐藏的固有并行性以及更好的全局最优化能力；通过概率优化方法能自动访问及引导到最优搜索区间，适应性地调整搜索方向，不需要建立规则[2]。它尤其适用于处理传统搜索难以解决的复杂和非线性问题，可广泛应用于组合优化、机器学习、自适应控制、规划设计和人工生命等领域。
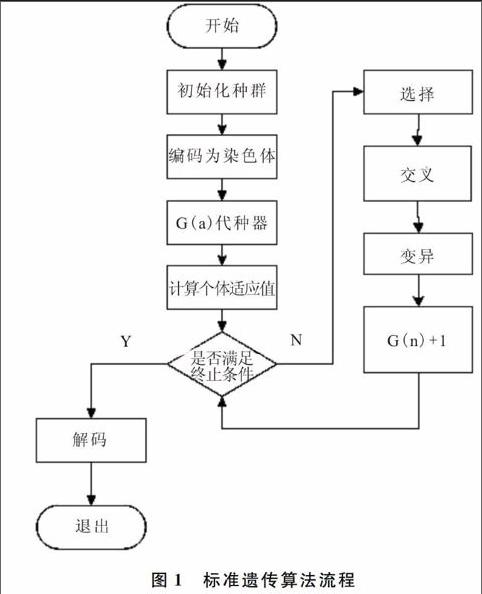
遗传算法可形式化描述为[3]GA={Γ，Pop，S，M，T，C，π}，其中Γ={x|f（x）}；设个体为Rani，，则Pop={Ran1，Ran2，…Rani，i∈（0，π）}；S={，i = 1，2，...N}；M表示突变算子；T表示终止条件；C表示交叉算子，π表示种群大小。遗传算法由选择算子、突变算子、交叉算子3个基本算子组成。通过这3个基本算子，可以从一个初始种群Pop出发，产生期望的改良种群。标准遗传算法流程如图1所示。
遗传算法中普遍存在进化停滞问题[4]。这意味着大量个体陷入局部极值，并且趋于一致，无法改进，也不能通过交叉操作或者突变操作来生成新个体。为改进这些缺点，本文通过改进遗传算法，提高种群搜索速度及保证收敛概率。
基础遗传算法的选择算子随机选择个体，没有目的性，很可能错过较优个体，而选择了较差个体，不利于后期操作。在交叉操作中，最简单的交叉操作是单点交叉，即选择种群中的两个个体，在个体的位串中随机选择交叉点，然后交换两个位串的尾部，形成两个新的个体。当参数数量增加时，位串长度也随之增加。只有单点交叉，位串的结构化改变很小，对于引进新的信息不具建设性，会降低搜索效率。突变操作是在一定概率下对个体进行变异，带有很强的不确定性，可能较优的个体经过突变后变差了，不利于优化。
编码是通过一个特殊字符串来展示目标问题的解，描述问题解空间以及遗传算法相应的编码空间。编码过程是遗传算法的基础，编码方法不仅仅决定个体染色体排列形式，还通过遗传算法空间的基因型到问题空间的表型来决定个体的编码方法。同时，编码方法也影响遗传算子的计算方法。
2 改进的遗传算法
本文使用最常见的二进制编码方法。二进制编码方法是遗传算法中最基本、最常用的编码方法。同时，二进制编码也是最小的编码单元，易于编码和解码，易于实现交叉和突变操作。
本文针对基础遗传算法的缺陷，依次对选择算子、交叉算子、突变算子3个算子进行改进，后续算子的改进建立在前面算子改进的基础上，并分别对改进进行实验。分别将3个改进的算法命名为SO（selection operator），SACO（selection and cross operator），SCAMO（selection cross and mutation operator）。
在SO算法中，本文通过适应度值来选择个体，选择适应度值高于平均值的个体，保持当前最优解；在SACO算法中，在SO的基础上，对于交叉算子，本文增加交叉点，将单点交叉改成多点交叉，交叉点可以落在每个参数的位串，实现每个参数位串中的单点交叉；在SCAMO算法中，在SACO的基础上，对于突变算子，采用基本的位突变，首先随机选择一个个体的一个变量，然后随机确定染色体代码对的可变点位置。不对每代都进行突变操作，只有在经过几代（比如经过四代）交叉操作后得到的最优个体没有改变的情况下，才对这个新种群进行突变。代表性地，突变控制的一般值为0.001～0.1。
选择适应性函数直接影响遗传算法的收敛速度和找到最优解的能力，遗传算法评价一个解的好坏不仅取决于其解的结构，而且取决于相应解的适应值。因此，根据实验问题要求，设计适应性函数如下：
f=63￡+∑3i=1fi（1）
其中f1，f2，f3是插装程序的分支函数。
改进的遗传算法3个算法描述如下：
SO：根据适应值高低选择个体，即对整个种群求其平均值，选择适应度值高于平均值的个体，淘汰适应度值低于平均值的个体；
SACO：在SO的基础上，保留当前最优的两个个体，不对其进行交叉操作。对两两个体中的染色体进行多位交换（本文假设进行三位交换），然后将染色体位串平均分成3等份，对各等份中的染色体进行随机定位交换。
SCAMO：在SACO的基础上，对每代经过交叉后生成的新种群进行审查，并记录代数。如果经过一定代数选择操作后，生成新种群中的最优个体没有变化，则对其进行随机位突变操作。
根据上述算法描述，相应代码（只展示不同于其它算法的部分）如下：
2.1 选择算子算法
Function selectionOperator（）
n←0；//初始化种群n
fit[]←{0}；//初始化适应度值数组
for each 个体 in 种群
fit[i] ←f（i）；
avg←sum（fit[i]）/n //求种群的平均值
EndFor
newPop[]←{0}；//初始化空种群newPop；
for each 个体 in 种群
if （f（i） > = avg）
newPop.add（f（i））；//将i个体加入到newPop中；
EndFor
EndFunction
2.2 交叉算子算法
Function crossOperator
for each 个体 in 要用来交叉的个体数 //交叉个体数根据交叉概率计算
rand←Random.next %total； //total为种群中全部个体适应度值的和
if（rand <=f（i） and rand<=f（i+1）） //如果第i个个体的和第i+1个个体的适应度值大于随机值rand，就对这两个进行交叉操作
for each 参数 in 组成位串的参数个数n
for each 基因 in 参数染色体长度//范围从rand到染色体长度，即z=rand
//将第i个个体组成染色体的第j组参数从z到参数染色体末尾与第i+1个体进行交换
newPop[i].chromosome[j*n+z]？ newPop[i+1].chromosome[j*n+z]；
EndFor
EndFor
i++；
EndFor
EndFunction
2.3 突变算子算法
Function mutationOperator（）
n←0； //n为算法中根据实际情况设置的允许最高适应度值相等的代数
if（maxNumber[i]到maxNumber[i+n]之间的n个值相等） //如果在存放最大值的数组中，连续n个值相等，则进行突变操作
for each 个体 in 新种群 // newPop中的种群进行给定概率的突变
rand←Random.next；
if（newPop[z].chromsome[rand]=1）
newPop[z].chromsome[rand]←0；
if（newPop[z].chromsome[rand]=0）
newPop[z].chromsome[rand]←1；
EndFor
EndFunction
通过上述改进，使选择过程有目的性，为后续操作提供有利条件；让交叉操作在每个参数的位串上更有效率，并且充分发挥交叉的力量，改善搜索的效率；使得突变操作减少不可控性，可以更加迅速的朝有利方向趋近。
3 实验研究
为证明改进遗传算法生成测试用例相对于基本遗传算法的优越性和有效性，在win7系统上，用Java语言编写改进的遗传算法。以三角形判别问题作为被检测程序，检验算法运行效果。在诸多软件测试研究中都将三角形分类程序作为一个基准程序来使用，Berndt[5]、Michael[6]、Wegener[7]、Lin and Yeh[8]等都在使用遗传算法进行路径测试的研究中使用三角形问题作为检验测试用例生成例程。此程序中输入的参数是组成三角形的三条边，范围为[0，63]。通常选择几个分支组成一个路径作为程序测试的主要目标。本文选择等边三角形作为输出路径，因为等边三角形的路径是最难的，而且对于此程序，其被搜索的概率为25/（25）3=2-10，这意味着如果用随机方法生成子代，3个相等的边直到子代生成次数超过一千多次时才会生成远远多于其它路径。
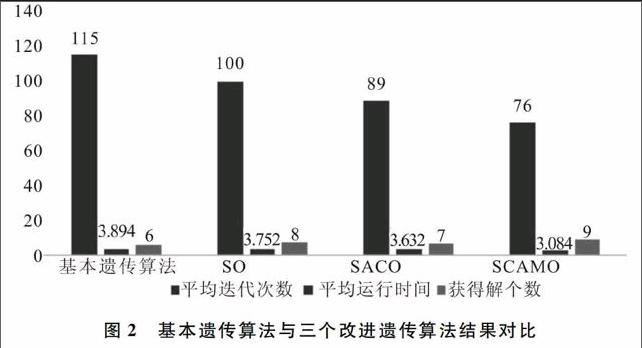
试验中，首先分析过程和测试程序的路径，然后插装到程序中，并且分别设置参数，分别用基本遗传算法和改进遗传算法来生成10个等边三角形测试用例，当生成测试用例时记录迭代数量G，执行时间T以及获得正确解的个数，并计算平均运行代数以及平均运行时间，获得解的个数作为衡量算法效率的主要指标[10]。结果如图2所示（种群大小：500，最大跌代数：300，交叉概率0.7，突变概率0.05，路径：等边三角形）。
从改进结果可以看出，改进的遗传算法不论是在运行代数、运行时间，还是解的个数看，都远远优于基本遗传算法。
4 结语
本文探讨了基本遗传算法的准则，并针对遗传算法的缺点进行改进，通过实验证明改进的遗传算法相对于基本遗传算法的优越性。由于交叉操作和突变操作存在一定的不可控性，可能导致算法在运行一定的代数内得不到解。下一步将着重研究从基本遗传算法的每个要素上最大限度减少交叉操作和突变操作中带来的不可控性，提高效率。
参考文献：
[1] P MCMINN. Search-based software test data generation：a survey，software testing[J]. Verification and Reliability， 2004（56）：105-156.
[2] KOREL B. Automated software test data generation [J]. IEEE Trans on Software Engineering， 1990， 16（8） ：870-879.
[3] 张文修，梁怡.遗传算法的数学基础（第二版） [M].西安：西安交通大学出版社，2003（5）：125-129.
[4] 玄光南.遗传算法与工程化 [M].北京：清华大学出版社，2004：62-74.
[5] BERNDT D， FISHER J， JOHSON ，et al. Breeding software test cases with genetic algorithms[C]. 36th annual Hawaii Int. Conference on System Sciences（HICSS03），2003：16-22.
[6] MICHAEL C， MCGRAW G， SCHATZ M. Generating software test data by evolution[J]. IEEE Transactions On Software Engineering， 2001， 27（12）：11-18.
[7] WEGENER J， BARESEL A， STHAMER H. Evolutionary test environment for automatic structural testing[J]. Information and Software Technology， 2001， 43（14）： 841-854.
[8] BORGELT K. Software test data generation from a genetic algorithm[M]. CRC Press 1998：23-28.
[9 ] 汪浩，谢军凯，高仲仪.遗传算法及其在软件测试数据生成中的应用研究[J].计算机工程与应用，2001（12）：64-68.
[10] 伦立军，丁雪梅.基于遗传算法的测试数据生成研究[J].微机发展，2005（12）：76-84.
（责任编辑：陈福时）
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2025/2/6 2:07:39