网站首页  词典首页

请输入您要查询的论文：

　

标题 是什么？为什么？怎么办？
范文 陈卓英




[摘 要]几何直观作为《义务教育数学课程标准（2011年版）》的核心概念之一，在数学学习中有着重要的地位和意义，无论是在图形与几何领域，还是其他知识领域的教学中，都应重视几何直观的培养。从几何直观是什么，为什么要重视几何直观的培养，到几何直观在小学数学教学中怎么培养这三方面进行梳理，论述渗透几何直观的价值、意义以及方法。
[关键词]几何直观；小学数学教学；本质；价值；教学策略
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2018）05-0019-03
当下，有关几何直观的讨论是个热点，但如同“什么是数学”没有完美的答案一样，对几何直观的理解也是仁者见仁，智者见智。这里，让我们按“几何直观是什么→为什么要重视几何直观的培养→几何直观怎么培养”的顺序开始梳理。
是什么？──品味“几何直观”的本质
对于比较抽象的数学概念、容易混淆的数量关系，学生思考时需要借助直观形象。因此，教师就需要将这些问题与直观形象的图形结合起来，以“形”助“数”，为学生解决问题提供具体经验的支撑。那么什么是几何直观呢？关于几何直观及其意义，《义务教育数学课程标准（2011年版）》是这样论述的：“几何直观主要是指利用图形描述和分析问题。借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果。几何直观可以帮助学生直观地理解数学，在整个数学学习过程中都发挥着重要作用。”
一、“几何直观”与“图形与几何”
几何直观，是课程标准增加的核心概念之一。几何内容的教学，既可以培养学生的逻辑推理能力，又能培養学生的直觉思维能力。在“图形与几何”的学习过程中，对物体或图形的观察，形象思维的形成和想象，都包含着几何直观的因素。几何直观来源于“图形与几何”，“图形与几何”是一个学习范畴，几何直观是一种学习能力。许多数学概念都具有“数”与“形”的两个特征，要深入地理解它们的本质，就要从“数”与“形”两个角度去认识和把握。因此，学会用图形思考和想象是学习数学的基本能力，教师要重视学生这方面能力的培养。
二、“几何直观”与“空间观念”
几何直观与空间观念作为“图形与几何”的代名词，分别从不同角度覆盖了几何学习的重要目标，二者既有重叠之处又各有侧重。
几何直观往往是在有背景的条件下，借助直观图形“看”出来的结果，通常需要逻辑推理的证明。空间观念则偏重于“想象物体的方位以及物体之间的位置关系”“描述图形的运动和变化”“依据语言描述画出图形”等，这些活动不一定需要凭借看得见、摸得着的真实图形，凭借语言或想象也是可以的。
几何直观侧重于利用图形整体把握问题，更接近应用层面；空间观念侧重于学习者对于空间的感知和把握，涉及运用图形的能力，更注重几何学习给学生带来的变化和发展。
三、“几何直观”与“数形结合”
数形结合是一种基本的数学思想方法。它是指解决数学问题时，通过数与形之间的对应和转化来解决数学问题。几何直观主要是利用图形描述和分析问题，从而帮助学生直观地理解数学知识。如比较分数1/4和1/5的大小，当学生接触到“把一个圆平均分成四份，其中的一份与平均分成五份中的一份相比”时，生活经验首先介入，然后支撑表象马上建立，于是“大于”的结果直接就在学生头脑中形成了。显然，几何直观的内涵最重要之处是直接感知，和数形结合是有区别的。
数形结合更多的是将具体的解决问题的策略与方法呈现在我们面前，可以“由形到数”，也可以“由数而形”。几何直观只有“由形到数”这一方面，从某种程度上讲，它也可以被认为是一种能力。从这个角度看，几何直观比起空间观念和数形结合，它的意义更为深远，值得教师在教学中加以强调。
为什么？──把握“几何直观”的价值
几何直观在帮助学生发展空间观念、提升思维能力、找到解题策略等方面有着很大的价值。
一、发展空间观念
几何直观是一种思维方式，它是以几何图形为载体进行推理论证的。因此，几何直观可以培养学生的空间感，发展学生的空间观念。
二、提升思维能力
几何直观可以丰富学生头脑中的表象，以直观认识、判断和表象作为想象力的基础，还能不断培养学生的形象思维能力，为学生创造性思维和逻辑思维的培养做好充分准备。
1.形象思维能力的训练
小学生的思维正处于以形象思维为主的阶段，他们思维的形象性与数学知识的抽象性之间的矛盾正需要通过几何直观来化解。
比如在学习自然数时，学生发现：自然数就像射线，只有一个端点，从这个端点出发可向外无限延长，没有终点。学生的这个发现把自然数和射线巧妙地联系起来，连接数与代数中的自然数概念和图形与几何中的射线，缩短了知识间的距离。
2.培养逻辑推理能力
逻辑思维是其他数学思维的基础，是数学素养的重要表现。小学生受思维特点、语言水平的限制，几乎都是通过图形或是借助想象来培养自身的逻辑推理能力。教师在教学运算定律、分数的基本性质等内容时，就可以通过几何直观实现合理解释和说理，以培养学生初步的逻辑思维能力。
3.提升创新思维能力
创新思维的关键是直觉思维。几何直观具有极大的启发性，常常可以指引数学发现的方向，在教学中利用好几何直观，有助于学生整体把握学习对象，简化思维过程，提升创新思维能力。
三、找到解题策略
在数学学习中，学生可以通过图形刻画和描述问题，把问题变得简单和直观。几何直观作为核心概念，对学生把握数学思想和恰当运用数学知识与方法解决问题是不可或缺的。几何直观还可以培养学生的洞察力，帮助学生迅速找到解题策略。
怎么办？──探索“几何直观”的教学策略
随着年级的升高和知识难度的加深，高年级学生的思维水平处于由具体运算向形式运算过渡的阶段，几何直观可以帮助他们更好地理解和学习数学。在小学数学教学中，要从直观教学入手，引导学生运用画图策略分析问题，将直观图形与数学语言、符号语言进行合理转换，在解决数学问题的过程中感悟数与形、形与数之间的转化，让几何直观的培养贯穿于整个教学过程。下面就以人教版五年级的教学为例进行论述。
一、几何直观在“图形与几何”领域中的应用
在“图形与几何”领域的教学中，教师要强调“几何”的方法，但不一定要提到“直观”。幾何方面的学习对象本身就有直观性，所以不必再强调用了“直观”的方法，反而可以多强调“空间观念”。
【策略1】化静为动重体验
五年级下册“图形的运动”中的“旋转”是一个教学难点。通过操作活动，化静为动，能让图形变换的教学更有效。在学生掌握了旋转三要素（旋转中心、旋转方向和旋转角度）后，借助实物旋转进行教学，不失为一个有效的方法。对于那些三角形状的旋转图形，可以借用实物来帮助思考，如三角尺、三角小旗等，引导学生把三角尺按顺时针或逆时针方向旋转相应的角度，再想办法把实物旋转后的位置画在方格纸上。当然，旋转的最高境界自然是“无招胜有招”，用实物代替只是教学初始阶段使用的方法。学生只有真正掌握旋转的要素，才能准确、迅速、美观地画出旋转后的图形。
【策略2】化看为思定模型
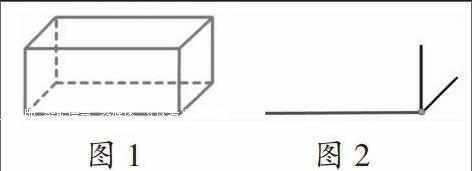
几何直观就是“依托、利用图形进行数学的思考和想象”。教学时，教师要注重引导启发，让学生利用几何直观“描述与分析问题”，从而发现数学的本质和规律。如教学“长方体和正方体的认识”时，在学生初识长方体和正方体的特征后，为了让他们能将活动经验真正转化为有效的数学知识，教师可先用课件呈现长方体的透视图（如图1），并提问：“如果擦去其中的一条棱，你还能想象出这个长方体的大小吗？”
学生擦去其中的一条棱，发现仍能想象出长方体的大小。教师再问：“至少要留下哪几条棱，才能保证我们还可以想象出长方体的大小？先想一想，再动手试一试。”结果多数学生在尝试后留下了相交于一个顶点的长、宽、高三条棱（如图2）。这样，学生在“观察─操作─想象”的过程中提高了几何直观能力。
二、几何直观在非图形与几何领域中的应用
在非图形与几何领域中，如“数与代数”，教师要将教学锁定于“直观”，但不一定要提到“几何”。这是因为，在数学的学习领域中，能做到直观的不只“几何”一个。同时，因为强调直观，学生会应用表格、数轴、示意图等带有几何特色的方法。当学生喜欢使用他认为直观的方法时，几何直观就已经渗透于其中。
【策略1】数形结合促理解
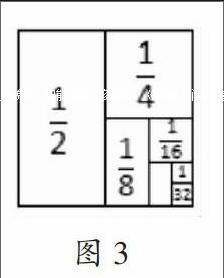
在教学分数及其运算时，为了帮助学生理解分数的意义，可以借助“面积模型”将抽象的思维过程直观形象化。如五年级下册的分数运算中的一道题目：有一杯水，第一次喝了半杯，第二次又喝了剩下的一半，就这样每次都喝了上一次剩下的一半，五次一共喝了多少水？此题实际上就是求“1/2+1/4+1/8+1/16+1/32=？”，但如果直接计算，显然十分烦琐。这里，教师就应向学生渗透数形结合思想：先画一个正方形（如图3），并假设它的面积为单位“1”，由图可知，“1-1/32”就是所要求的结果。
【策略2】化繁为简露本质
如五年级下册的“打电话”题目：学校合唱队有15人，暑假有紧急演出，教师要尽快通知每个队员，用打电话的方式，每分钟通知1人，最少需要多少分钟？一图抵百语，图4就能简明扼要地呈现“打电话”这个复杂的问题。
有了这个图，学生就能发现规律：每次新接到通知队员数都是前一分钟接到通知队员数的2倍。讲不清、算不出，看图却很明了。可见，借助几何直观，能帮助学生探究问题内在的规律，化繁为简，从而找到解决问题的思路和方法。
【策略3】化隐为显巧作图
在解决问题的过程中，借助画图进行分析，往往能将抽象的问题变得形象直观，化隐为显，使学生豁然开朗，获得“柳暗花明又一村”的体验。
如五年级上册的“植树问题”：同学们在全长100米的小路一边植树，每隔5米栽一棵（两端要栽）。一共要栽多少棵树？为了方便学生画图交流，教师把“100米长的小路”改成“20米长的小路”，教学时先让学生在纸上模拟栽树（如图5），通过图形直观地找出各数量之间的关系，探寻解决问题的方法：因为20里有4个5，所以有4个间隔，得出“间隔数=总长÷间隔长”。由线段图可知“每个间隔栽1棵，一共栽5棵”，从而发现数量关系“两端都栽时，棵数=间隔数+1”。这样通过形的直观，加强了形与数之间的转换，把抽象的数学问题直观化。
“让学生养成画图的习惯，脑子里要留下一些图形”，这是教师一直要做的。教师要鼓励学生多角度思考，引导学生优化方法，带领学生在个性化方法和数学通法之间，在想象和理性思考之间鹰击长空、鱼翔浅底。
（责编 金 铃）
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2024/12/23 4:10:06