网站首页  词典首页

请输入您要查询的论文：

　

标题 基于泊松过程可分解性的小区开放对道路通行能力的影响
范文 范英兵+田晶+高颖+李明惠



摘要：基于泊松过程的可分解性，分析道路通行能力影响因子，建立车辆通行的数学模型，以研究小区开放对周边道路通行的影响。利用VISSIM软件对树状小区的交通情况进行模拟得到各指标值，得出开放的树状小区内的道路运行能力改善程度，同时定量比较环状小区和网状小区周边主干道的畅通能力改善程度。
关键词：泊松过程；小区开放；道路通行能力
中图分类号：TP319
文献标识码： A
文章编号： 16727800（2017）004015603
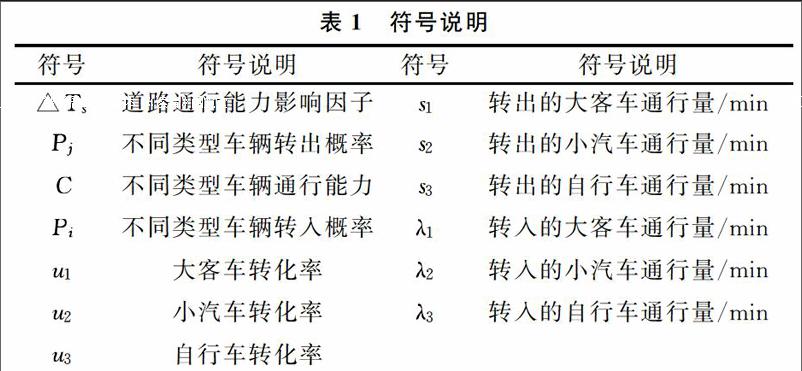
0引言 伴随着经济的快速发展和社会的全面进步，快速城市化进程也使各种社会问题和社会矛盾日益凸显。封闭住区带来的城市环境与社会问题为人所诟病。在现实生活中，开放式小区除了存在安全、噪音等问题外，人们对开放式小区能否优化路网结构、提高道路通行能力、改善交通状况有着不同观点。因此，本文提出两个问题：①建立关于车辆通行的数学模型，用于研究小区开放对周边道路通行的影响；②小区开放产生的效果与诸多因素有关，要求选取或构建不同类型的小区，根据建立的模型定量比较各类型小区开放前后对道路通行的影响。1模型假设 假设如下：①假设选取的车道符合理想条件，即天气晴朗，风力小于3级，确保所选道路在道路条件和天气环境条件方面的可比性； ②车流量、人流量和速度数据没有受到天气影响； ③为了计算方便，不考虑所选路段车流中各类车型的比例； ④小区附近主干道的交通运行能力相等； ⑤小区内的道路可以承受交通运行； ⑥假设道路基本通行能力C=1。2符号说明本文符号说明见表1。
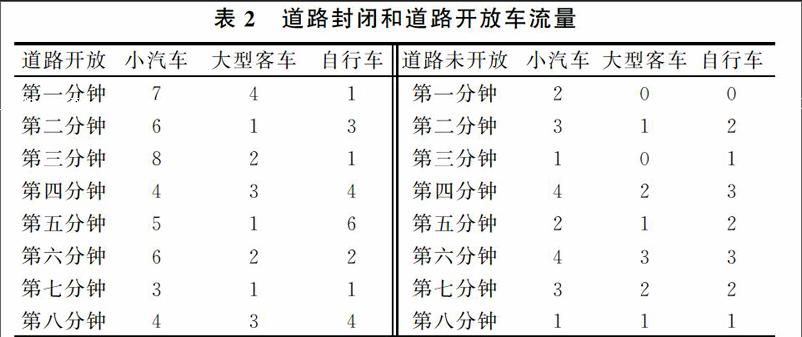
3问题分析3.1问题一建立车辆的数学模型需要有关车辆在具体时间段、特定地点的车辆通行数据。利用VISSIM软件在特定路段（开放小区两个不相邻的十字路口）内动态模拟特定时间测量的车辆流量数。通过模拟数据，计算各类型道路的实际道路运行能力即车辆转弯概率，建立基于Poisson过程的车辆通行数学模型，用于研究小区开放对周边道路通行的影响。通过道路通行能力影响因子，即开放小区后道路运行饱和度的改变量，反映开放小区对道路通行的影响程度。3.2问题二〖JP2〗根据不同的小区结构和道路结构研究小区开放前后对道路的影响。首先选取两个不同类型的道路结构，将未开放内部的道路封闭，利用VISSIM软件模拟各指标值，利用基于Poisson过程的车辆通行数学模型进行计算，将未开放小区与开放小区的道路运行饱和度进行对比，并考虑小区内道路的结构及运行能力，给出各类小区的开放条件。〖JP〗4模型建立与问题解决4.1问题一〖BT3〗4.1.1数据预处理采用微观交通软件VISSIM获取各种车辆数据，该软件有较强的灵活性，在特定的小区区域内，建立道路宽度、车的类型等信息，然后建立道路交点，结合VISSIM得出3D的两个简化道路的车流量情况，通过视频，得出了车型、流量等数据。根据该软件，模拟得到8分钟通过的车辆数量分别为小汽车63辆、大型客车26辆、自行车36辆，具体区域道路封闭和开放相关数据如表2所示。
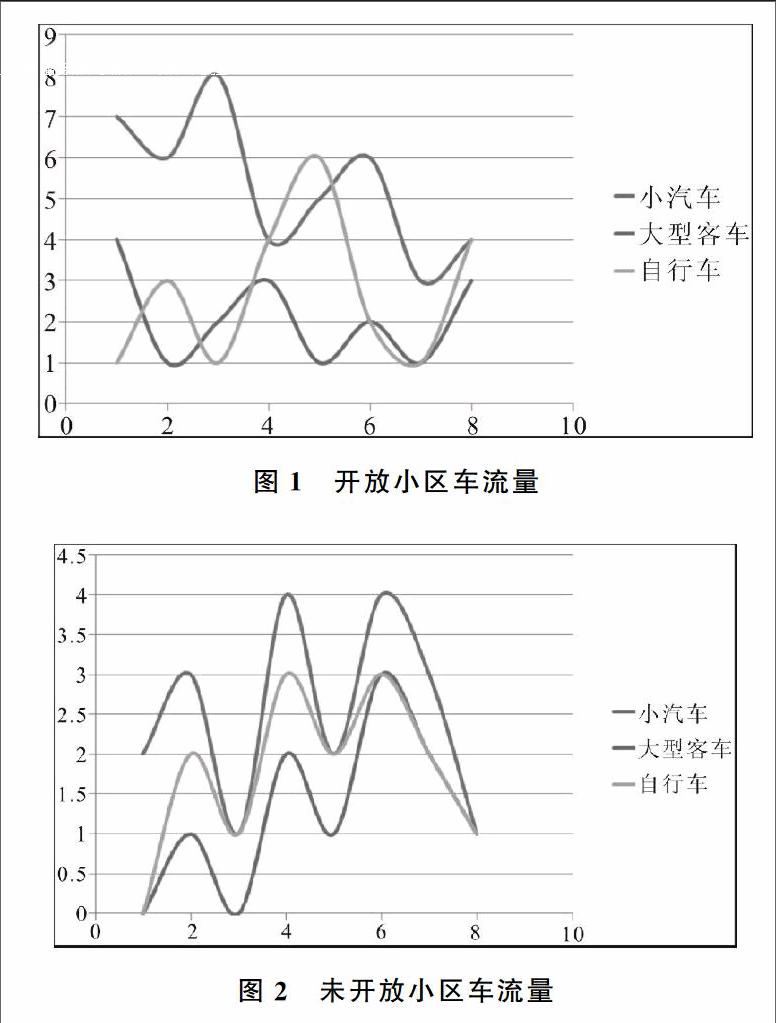
开放前后的各类车流量具体变化情况如图1、图2所示。由此得到开放小区后对小汽车、自行车、大型客车的车流量改变显著。
4.1.2数据分析
本文选择的小区为两个十字路口，利用Poisson过程这一随机过程，符合VISSIM软件随机生成的数，观测出单位时间内各类车辆各个方向转弯的计数，作为单位时间内的λ（强度），以比较小区开放和未开放对周边道路通行的影响。
根据VISSIM软件观测各类车辆在主十字路口转向的数量，作为Poisson过程λ的系数，即小区开放得到每分钟内不同类型车辆通过的数量如表3所示。通过各方向汽车转弯车流量与总车流量的比值计算各方向的车辆转弯概率如表4所示。
4.1.3模型建立在文献[1]中的11个指标中，饱和度的权重最大，所以选用饱和度变化来衡量小区开放前后对道路通行的影响，并将其作为道路通行影响因子。设车流量强度为λ的过程穿过未开放小区，每次穿过小区按不同方向行驶的概率为Pi，且开往各方向的线路相互独立，也与其它到达行为独立。用Ni（t）表示[0，t]内穿过未开放小区的次数，{Ni（t）}是强度λi=piλ的泊松过程，当p1+p2+…+pn=1时，n个泊松过程相互独立。符号说明如表5所示。
由于小区未开放和开放的道路通行结构不一样，计算出开放前各类车辆道路行驶的概率。小区开放后的道路数量增加，则会对各个方向的概率产生影响，即为泊松过程的可分解性。根据泊松过程可分解性的方法，对各个因素进行分析，得到车辆通行能力影响因子△Ts的数学模型，以研究小区开放对周边道路通行的影响。
树形结构小区的模拟图如图3所示，树形结构小区的车型、车流量等数据如表6、表7所示。
根据模拟数据，计算出小汽车向左行驶的概率为p=（2063SX）≈0.3，向右行驶的概率为p=SX（2063SX）≈0.3，直线行驶的概率p=SX（2263SX）≈0.35，调头行驶的概率p=SX（163SX）≈0.05。由此方法同样可得大型客车及自行车按不同方向行驶的概率。根据我国现行公路交通量调查中对不同类型车辆的折算系数表，查得各类型汽车换算率分别为：小汽车u1=0.5，大型客车u2=1，自行车u3=0.1。根据该模拟数据可得，小汽车转入的流通量λ1=7.3，大型客车转入的流通量λ2=5.2，自行车转入的流通量λ3=8.4，小汽车转出的流通量s1=9，大型客车转出的流通量s2=6.5，自行车转出的流通量s3=7.2。因此，根据模型得到树形结构小区的通行能力影响因子△Ts=0.299 5，此方案是如果A道路通行能力低于B道路通行能力，对小区道路C开放将造成很大影响；如果B道路通行能力低于A道路通行能力，对道路C开放则没有太大影响。已知小区道路C的计算结果为0.046，当其满足一定通行量时，才可以开放。开放后计算得到结果为-1.928 5，因此将会对小区造成更严重的交通堵塞。当A道路的承运能力低于B道路时，开放小区对交通缓解效果显著；当A道路的承运能力不低于B道路时，开放小区对交通承运能力缓解效果一般。4.2问题二根据小区的不同结构及进出口节点个数，将小区分为环形结构小区（见图4）、网状小区（见图5），研究小区开放对周边道路通行能力的影响。先对环形小区开放时周边道路的交通能力进行计算，根据该模拟的数据表8、表9，可以计算出小汽车向左（右）行驶的概率为p=SX（3485SX）≈0.4，直行概率为p=SX（4785SX）≈0.55，调头概率为p=SX（485SX）≈0.04， 由此方法也可得大型客车及自行车按不同方向行驶的概率。小汽车转入的流通量λ1=8.7，大型客車转入的流通量λ2=6.3，自行车转入的流通量λ3=6.9；小汽车转出的流通量s1=9，大型客车转出的流通量s2=6.4，自行车转出的流通量s3=7.1。
根据模型计算得到环形周围路段A和路段B的值分别为0.15和0.17，而环形路段的值为-0.38。说明只有在路段C有足够的通行量时，才能开放小区。同理，对网状小区开放时周边道路交通能力计算得到的结果如下：经过计算得出路段B的值为-0.28，路段A和路段C的值为0.17和0.11。因此，只有当路段B的流通量大时，小区才可以开通。5模型评价与推广 模型优点：VISSIM模拟了多种控制信号（SCOOT、SCATS），因而非常适合城市交通系统的仿真，同时它还可对路网中车辆的行驶情况进行2D和3D动画展示。VISSIM软件交通模型的描述精度高，而且所模拟的交通具有多样性。模型缺点：VISSIM对计算机硬件资源消耗较大，因而对计算机硬件要求比较高，同时它还存在对其它ITS技术支持不足的问题。而且在设置权重时主观性较强，设置指标的权重会间接影响最终的决策结果。指标过多时，数据统计量大，且权重难以确定。由于时间关系，调查数据有限，本文只是简单比较了两种不同类型的小区。 基于泊松过程可分解性的交通能力模型主要应用于立交桥通行、系统可靠性、保险风险预测等研究领域。
参考文献：[1]YB FAN，LN SUN. Based on hierarchy analysis method of evaluation of the village roads open[J].Journal of Computing Science and Engineering，2016.
[2]Special report 87：highway capacity manual[R].Washington D C. TRB.National Research.Council，2012：109120.
[3]王波.城市道路交叉口交通组织与信号控制策略研究[D].长春：吉林大学，2009，41（9）：17061713.
[4]黄秀彤.城市小区的善治之道[D].厦门：厦门大学，2014.
[5]张国颖.创新社会背景下开放式社区管理探索[D].济南：山东大学，2012.
[6]王筱祯.我国城市社区多元共治问题研究[D].济南：山东大学，2011.
（责任编辑：黄健）
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2024/12/22 22:01:20